Çoxbucaqlı ☰

Çoxbucaqlı iki ölçülü həndəsi fiqurdur və qapalı forma yaratmaq üçün ucdan uca birləşdirilən sonlu sayda xətt seqmentlərindən (yanlar və ya kənarlar adlanır) ibarətdir. "Çoxbucaqlı" sözü yunanca "poly" ("çox" deməkdir) və "gon" ("bucaq" deməkdir) sözlərindən yaranmışdır.
Çoxbucaqlıların istənilən sayda tərəfi ola bilər, lakin onlar düz xətlər olmalıdır və kəsişməməlidir. Üç tərəfi olan çoxbucaqlılara üçbucaq, dörd tərəfi olan çoxbucaqlılara dördbucaqlı, beş tərəfi olan çoxbucaqlılara beşbucaqlılar və s. deyilir.
Çoxbucaqlının perimetri onun tərəflərinin uzunluqlarının cəmidir.
Əgər çoxbucaqlının \(n\) tərəfi varsa və hər tərəfin uzunluğu \(i = 1,2,…,n\) üçün \(s_i\) ilə işarələnirsə, o zaman \(P\) perimetri belə verilir:
\( P = s_1 + s_2 + \ldots + s_n = \sum_{i=1}^n s_i\)

Tərəflərinin ucları çoxbucaqlının təpə nöqtələrdirir. Çoxbucaqlı onun təpələrini göstərən hərflərlə adlandırılır.

Çoxbucaqlı aid olduğu müstəvinin nöqtələrini iki çoxluğa ayırır: çoxbucaqlının daxilində olan sonlu hissə və onun xaricində qalan sonsuz hissə.


Çoxbucaqlılar qabarıq və çökük ola bilər.

• Qabarıq çoxbucaqlı istənilən tərəfini saxlayan düz xəttin ayırdığı yarımmüstəvilərdən birində yerləşir.
• Çökük çoxbucaqlı heç olmasa bir tərəfindən keçən düz xəttin ayırdığı müxtəlif yarımmüstəvilərdə yerləşir.

Qabarıq çoxbucaqlının daxilində götürülmüş istənilən iki nöqtəni birləşdirən parça bütövlükdə çoxbucaqlının daxilində yerləşir.
Qabarıq çoxbucaqlının verilmiş təpədən çıxan iki tərəfinin əmələ gətirdiyi və çoxbucaqlının daxil olduğu bucağa, həmin təpədəki daxili bucaq deyilir. Qabarıq çoxbucaqlının daxili bucağına qonşu olan bucağa çoxbucaqlının xarici bucağı deyilir.
Qabarıq çoxbucaqlının istənilən təpəsindəki daxili və xarici bucaqlarının (hər təpədəki xarici bucaqlardn biri götürülməklə) cəmi 180 dərəcəyə bərabərdir.
Bütün tərəfləri və bütün bucaqları konqruyent olan çoxbucaqlı düzgün çoxbucaqlı adlanır.

Qabarıq çoxbucaqlının daxili və xarici bucaqlarının cəmi ☰

Teorem 1. Qabarıq \(n\)-bucaqlının daxili bucaqlarının cəmi \( 180^\circ \cdot (n-2) \)-yə bərabərdir \( (n \ge 3) \).
Düzgün \( n \)-bucaqlının hər bir daxili bucağı \( \frac{180^\circ \cdot (n-2)}{n} \) -ə bərabərdir.

Teorem 2. Qabarıq çoxbucaqlının xarici bucaqlarının cəmi 360 dərəcəyə bərabərdir. Düzgün \(n\)-bucaqlının hər bir xarici bucağı \( \frac{360^\circ}{n} \)-ə bərabərdir.

Çevrənin daxilinə və xaricinə çəkilmiş çoxbucaqlılar ☰

Çoxbucaqlının bütün təpələri çevrənin üzərində yerləşirsə, bu çoxbucaqlıya çevrə daxilinə çəkilmiş çoxbucaqlı, çevrəyə isə çoxbucaqlının xaricinə çəkilmiş çevrə deyilir.


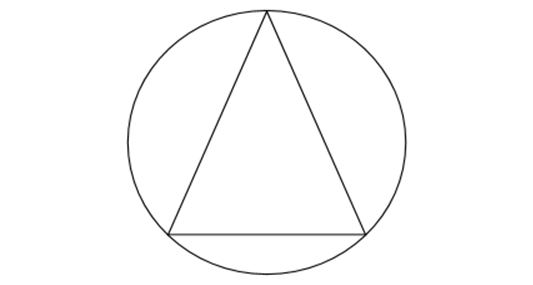
Çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çoxbucaqlıya çevrə xaricinə çəkilmiş çoxbucaqlı, çevrəyə isə çoxbucaqlının daxilinə çəkilmiş çevrə deyilir.

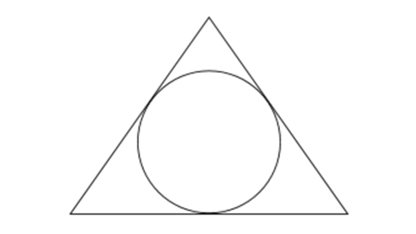
Üçbucağın daxilinə və xaricinə çəkilmiş çevrələr ☰

• Teorem 1. İstənilən üçbucağın daxilinə çevrə çəkmək olar. Bu çevrənin mərkəzi üçbucağın tənbölənlərinin kəsişmə nöqtəsidir.
• Teorem 2. İstənilən üçbucağın xaricinə çevrə çəkmək olar. Bu çevrənin mərkəzi üçbucağın tərəflərinin orta perpendikulyarlarının kəsişmə nöqtəsidir.
• Teorem 3. Çevrə daxilinə çəkilmiş üçbucaq düzbucaqlı üçbucaqdırsa, hipotenuz bu çevrənin diametridir.
• Tərs teorem. Çevrə daxilinə çəkilmiş üçbucağın tərəfi çevrənin diametridirsə, bu üçbucaq düzbucaqlı üçbucaqdır.
• Qeyd. Verilmiş üçbucağın xaricinə (və daxilinə) yalnız bir çevrə çəkmək olar. Verilmiş çevrənin daxilinə (və xaricinə) çəkilən üçbucaqlar isə sonsuz saydadır.

Çevrənin daxilinə və xaricinə çəkilmiş dördbucaqlının xassələri ☰

Üçbucaqlardan fərqli olaraq istənilən dördbucaqlının daxilinə və xaricinə çevrə çəkmək mümkün deyil.

Teorem 1. Çevrə xaricinə çəkilmiş dördbucaqlının qarşı tərəflərinin cəmi bərabərdir.
Tərs teorem. Dördbucaqlının qarşı tərəflərinin cəmi bərabərdirsə, onun daxilinə çevrə çəkmək olar.

Teorem 2. Çevrə daxilinə çəkilmiş dördbucaqlının qarşı bucaqlarının cəmi 180 dərəcəyə bərabərdir.
Tərs teorem. Dördbucaqlının qarşı bucaqlarının cəmi 180 dərəcəyə bərabərdirsə, onun xaricinə çevrə çəkmək olar.

Çevrənin daxilinə çəkilmiş dördbucaqlının sahəsi Brahmaqupta düsturu ilə hesablana bilər:
\( \text{Sahə} = \sqrt{(P-a)(P-b)(P-c)(P-d)} \), burada \(a\), \(b\), \(c\) və \(d\) tərəflərin uzunluqlarıdır.
\(P\) isə yarımperimetrdir, \( P = \frac{a+b+c+d}{2} \) ilə verilir.

Düzgün çoxbucaqlının daxilinə və xaricinə çəkilmiş çevrələr ☰

Düzgün çoxbucaqlı bütün tərəfləri və bucaqları konqruyent olan çoxbucaqlıdır. İstənilən düzgün çoxbucaqlının həm daxilinə, həm də xaricinə çevrə çəkmək olar və bu çevrənin mərkəzləri üst-üstə düşür.
Düzgün çoxbucaqlının xaricinə (və ya daxilinə) çəkilmiş çevrənin mərkəzi düzgün çoxbucaqlının mərkəzi adlanır. Düzgün çoxbucaqlının mərkəzi, tənbölənlərin kəsişmə nöqtəsi olub çoxbucaqlının bütün təpələrindən (və bütün tərəflərindən) bərabər məsafədədir.
Düzgün çoxbucaqlının mərkəzindən tərəfinə çəkilmiş perpendikulyara onun apofemi deyilir. Düzgün çoxbucaqlının apofemi daxilə çəkilmiş çevrənin radiusuna bərabərdir.

Düzgün çoxbucaqlının sahəsi ☰

Düzgün \(n\)-bucaqlının mərkəzini təpə nöqtələri ilə birləşdirdikdə \(n\) sayda konqruyent bərabəryanlı üçbucaqlar alınır.

\( S=\text{üçbucaqların sayı} \cdot \text{bir üçbucağın sahəsi}\)

\( S = n \cdot \frac{1}{2} ah = \frac{1}{2} (a \cdot n)h \) ; \( S = \frac{1}{2} Ph \) və ya \(S = \frac{1}{2} anh \).

Burada \(S\) çoxbucaqlının sahəsini, \(a\) tərəfinin uzunluğunu, \(n\) tərəflərinin sayını, \(h\) apofemini, \(P\) isə perimetrini bildirir.


Çevrənin daxilinə və xaricinə çəkilmiş çoxbucaqlının sahəsi üçün:
Daxilə çəkilmiş çevrənin radiusu \(r\), xaricə çəkilmiş çevrənin radiusu \(R\), düzgün çoxbucaqlının tərəfinin uzunluğu \(a\), çoxbucaqlının tərəflərinin sayı \(n\) olsun.

Bu halda:

Çevrənin xaricinə çəkilmiş düzgün çoxbucaqlının \(S\) sahəsinin düsturu:

\( S = \frac{1}{2} nr^2 sin \frac{2 \pi}{n} \) .


Çevrənin daxilinə çəkilmiş düzgün çoxbucaqlının \(S\) sahəsinin düsturu:

\( S = \frac{1}{2} nR^2 sin \frac{2 \pi}{n} \) .


Daxilə çəkilmiş çevrənin \(r\) radiusunu aşağıdakı düsturla hesablamaq olar:

\( r = \frac{a}{2 tg \frac{\pi}{n}} \) .


Xaricə çəkilmiş çevrənin \(R\) radiusunu aşağıdakı düsturla hesablamaq olar:

\( R = \frac{a}{2 sin \frac{\pi}{n}} \) .


Düzgün çoxbucaqlının \(P\) perimetri aşağıdakı kimi verilir:
\( P = an\).


Tərəflərinin sayı \(n\), tərəflərin uzunluğu \(a\) olan istənilən düzgün çoxbucaqlının sahəsi üçün düstur:

\( S= \frac{1}{4} n a^2 cot(\frac{\pi}{n}) \)