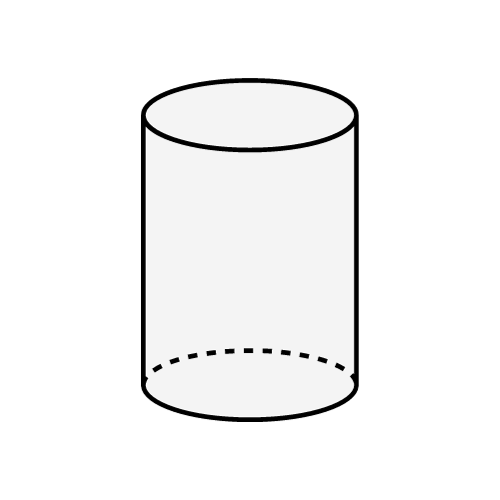
Fırlanma fiqurları ☰

Müstəvi fiqurun müəyyən ox ətrafında bir tam dövr fırlanmasından müxtəlif fəza fiqurları alınır. Bu oxa fırlanma oxu deyilir.
Kürə, konus, silindr bu cür fırlanmadan alınan fəza fiqurlarına sadə nümunələrdir.
Kürələr, konuslar və silindrlər də daxil olmaqla bir çox əyri fiqurlar, iki ölçülü formanı ox ətrafında fırlatmaqla yaradıla bilər. Bu formalara "fırlanma fiqurları" deyilir.

• Bir kürə onun diametri ətrafında yarımdairəni döndərməklə yaradıla bilər.
• Düzbucaqlı üçbucağı onun katetlərindən birinin ətrafında fırlatmaqla konus yaratmaq olar.
• Bir tərəfi ətrafında düzbucaqlını fırlatmaqla silindr yaradıla bilər.

Sferik həndəsə
Sferik həndəsə kürənin səthindəki fiqurları öyrənən qeyri-evklid həndəsəsidir. Bu həndəsə ənənəvi Evklid həndəsəsindən fərqlənir, çünki kürənin iki nöqtəsi arasındakı ən qısa məsafə düz xətt deyil, böyük dairə qövsüdür.

Sferik həndəsənin bəzi xassələri

• Sferik həndəsədə paralel xətlər yoxdur.
• Sferik üçbucağın bucaqları həmişə 180 dərəcədən çox olur.

Kürə ☰

Kürə, səthindəki bütün nöqtələri mərkəz adlanan sabit bir nöqtədən bərabər məsafədə olan mükəmməl simmetrik fırlanma fiqurudur. Mərkəzlə kürənin istənilən nöqtəsi arasındakı məsafəyə radius deyilir. Kürələrin sonsuz simmetriya xətləri və ən böyük həcm-səth nisbəti var ki, bu da onları istilik itkisini və ya buxarlanmanı minimuma endirmək üçün ideal edir.
Kürə səthinin istənilən iki nöqtəsini birləşdirən düz xətt parçasına kürənin vətəri, mərkəzdən keçən vətərə isə kürənin diametri deyilir.

Düsturlar:
Səthinin sahəsi (S): \( S = 4 \pi r^2 \)

Həcmi (V): \( V = \frac{4}{3} \pi r^3 \)

Diameteri (D): \( D=2r \)

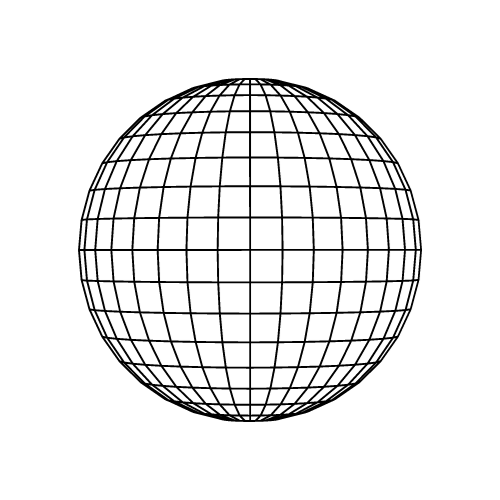
Xassələri

• Kürənin səthindəki bütün nöqtələr mərkəzdən bərabər məsafədədir. Kürənin səthi sferadır.
• Bir kürə müəyyən bir həcmə malik bütün fiqurlar arasında ən kiçik səth sahəsinə malikdir.
• Kürənin böyük dairəsi (great circle) onun səthinə çəkilə bilən ən böyük dairədir, dairənin müstəvisi kürənin mərkəzindən keçir.
• Kürə mükəmməl simmetrikdir və sonsuz simmetriya xətlərinə malikdir.
• Kürə istənilən həcmli fiqurlar arasında ən böyük həcm-səth nisbətinə malikdir və bu onu istilik itkisini və ya buxarlanmanı minimuma endirmək üçün ideal forma edir.

Real həyatdan nümunələr

• Planetlər və göy cisimləri tez-tez cazibə qüvvəsi ilə maddəni içəriyə çəkərək, ən az potensial enerji ilə forma əmələ gətirdiyinə görə təxminən sferik olurlar.
• Sferik çənlər propan kimi təzyiqli qazları saxlamaq üçün istifadə olunur, çünki onlar minimal gərginlik konsentrasiyası ilə yüksək təzyiqə tab gətirə bilirlər.

Konus ☰

Hər hansı müstəvi fiqurun nöqtələrini onun müstəvisinə aid olmayan nöqtə ilə birləşdirən bütün parçaların yaratdığı fəza fiquruna konus deyilir. Müstəvi fiqura konusun oturacağı, həmin nöqtəyə isə konusun təpə nöqtəsi deyilir. Konusun təpəsindən oturacaq müstəvisinə endirilmiş perpendikulyara konusun hündürlüyü deyilir. Oturacağı dairəvi olan konusa dairəvi konus, təpəsi oturacağının mərkəzinə perpendikulyar proyeksiyalanan dairəvi konusa isə düz dairəvi konus deyilir. Dairəvi konusun təpə nöqtəsini oturacaq çevrəsinin hər hansı nöqtəsi ilə birləşdirən parçaya konusun doğuranı deyilir. Bundan sonra konus dedikdə düz dairəvi konusu nəzərdə tutacağıq.
Konusun təpə nöqtələrindən və oturacağının mərkəzindən keçən düz xəttə konusun oxu, oturacağının radiusuna isə konusun radiusu deyilir.


Düsturlar
Səthinin sahəsi (S):
\( S_{\text{yan}} = \pi rl \)
\( S_{\text{tam}} = \pi r(r+l) \) burada \(r\) radius, \(l\) doğurandır.

Həcm (V): \( \frac{1}{3} \pi r^2 h \)

Doğuranı (l): \( l = \sqrt{r^2 +h^2 } \)

Kəsik konus, üst hissəni oturacağa paralel bir müstəvi ilə kəsməklə əldə edilən konusun bir hissəsidir.
Kəsik konusun səthinin sahəsi:
\( S_{\text{yan}} = 2 \pi rl \)
\( \small S_{\text{tam}} = \pi l (r_1 + r_2) + \pi r_1^2 + \pi r_2^2 = \pi (r_1 + r_2)l + \pi (r_1^2 + r_2^2) \)
Burada \(r_2\) böyük oturacağın radiusu, \(r_1\) kiçik oturacağın radiusudur.

Kəsik konusun həcmi (V) düsturla verilir:
\( V = \frac{1}{3} \pi h(R^2 + r^2 + Rr) \) Burada \(R\) böyük oturacağın radiusu, \(r\) kiçik oturacağın radiusu, \(h\) kəsik konusun hündürlüyüdür.

Tətbiqinə nümunələr

• Konuslar yollarda, raketlərin burun hissəsində və damlarda (konusvari dam örtükləri) istifadə olunur.
• Reflektiv konuslar və ya parabolik reflektorlar antenalarda, mikrofonlarda və teleskoplarda daxil olan dalğaları bir nöqtəyə yönəltmək üçün istifadə olunur.

Silindr ☰

Paralel müstəvilər üzərində yerləşən və paralel köçürmədə üst-üstə düşən iki konqruyent müstəvi fiqur və onların uyğun nöqtələrini birləşdirən bütün parçaların yaratdığı fəza fiquruna silindr deyilir. Bu müstəvi fiqurlar silindrin oturacaqları, onların uyğun nöqtələrini birləşdirən parçalar isə silindrin doğuranı adlanır. Doğuranı oturacaq müstəvisinə perpendikulyar olan silindrə düz silindr, əks halda mail silindr deyilir. Oturacaq müstəvilər arasındakı məsafəyə silindrin hündürlüyü deyilir.
Oturacağı dairə olan silindrə düz dairəvi silindr deyilir. Oturacaqdakı dairənin radiusuna silindrin radiusu deyilir. Düz dairəvi silindrin doğuranı hündürlüyünə bərabərdir. Bundan sonra silindr dedikdə düz dairəvi silindri nəzərdə tutacağıq.
Silindrin oturacağına paralel müstəvi ilə kəsiyi dairədir.
Silindr oxundan keçən müstəvi ilə kəsiyinə ox kəsiyi deyilir. Silindrin ox kəsiyi tərəfləri \(h=2r\) olan düzbucaqlıdır. Bu da \( S_{\text{oxkəs}} = 2rh \) deməkdir. Ox kəsiyi kvadrat olan silindrə bərabərtərəfli silindr deyilir. Silindrin oxuna paralel müstəvi ilə kəsiyi də düzbucaqlıdır.


Düsturlar
Səthinin sahəsi (S):
\( S_{\text{yan}} = 2 \pi rh \)
\( S_{\text{tam}} = 2 \pi r^2 + 2 \pi rh \)
Həcm (V): \( V = \pi r^2 h \)