Kvadratik funksiya və onun qrafiki
fərqlidir olduqda şəklində funksiyaya kvadratik funksiya deyilir. Burada , və əmsallardır.
Kvadratik funksiya bütün ədəd oxunda təyin olunmuşdur, yəni arqument istənilən həqiqi qiymət ala bilər.
Kvadrat funksiyanın qrafiki U formalı əyri olan paraboladır. Parabolanın istiqaməti əmsalının işarəsindən asılıdır. Əgər müsbət olarsa, parabola yuxarıya, mənfi olarsa, aşağıya doğru açılır.
Parabolanın simmetriya oxu vardır. Simmetriya oxu ilə parabolanın kəsişməsi təpə nöqtəsi adlanır.
Parabolanın təpə nöqtəsinin düsturu: .
Parabolanın simmetriya oxu tənliyi ilə verilmiş təpədən keçən şaquli xəttdir.
Kvadrat funksiyanın -kəsiciləri (sıfırları) kvadrat düsturla verilir: .
Əgər diskriminantı müsbətdirsə, kvadrat funksiyanın iki fərqli həqiqi kökü var, bunlar kəsişmələrinin koordinatlarıdır. Diskriminant sıfırdırsa, kvadrat funksiyanın təpə nöqtəsinin koordinatı olan bir həqiqi kökü olur. Diskriminant mənfi olarsa, kvadrat funksiyanın həqiqi kökləri yoxdur, lakin iki mürəkkəb birləşmə kökləri var.
Kvadrat funksiyaların absis oxu ilə kəsişmə nöqtələrinə görə yazılış forması:
, burada və kvadrat funksiyanın kökləridir. Simmetriya oxu ucları və olan parçanın orta perpendikulyarıdır. Təpə nöqtəsinin absisi . Bu forma funksiyanın köklərini tapmaq üçün faydalıdır.
Təpə nöqtəsinə görə yazılış forması:
, burada parabolanın təpə nöqtəsidir. Simmetriya oxu . Funksiyanın qrafikinin absis oxu üzərində olan nöqtələrində funksiyanın qiyməti 0-a bərabər olur. Arqumentin funksiyanı sıfıra çevirən qiymətləri bu funksiyanın sıfırları adlanır. -nın qiymətinə görə parabolanın təpə nöqtəsinin absis oxundan yuxarıda, aşağıda və ya absis
oxu üzərində olduğunu müəyyən etmək olar. olduqda təpə nöqtəsi oxundan aşağıdadır. olduqda təpə nöqtəsi oxu üzərindədir. olduqda oxundan yuxarıdadır.
Maksimum və minimum qiymətlər:
Əgər olarsa, parabola yuxarıya doğru açılır və təpə nöqtəsinin ordinatı funksiyanın minimum nöqtəsidir. Minimum qiymət -dır. Əgər olarsa, parabola aşağıya doğru açılır və təpə nöqtəsinin ordinatı funksiyanın maksimum nöqtəsidir. Maksimum qiymət -dır.
Təyin oblastı və qiymətlər çoxluğu:
Kvadrat funksiyanın təyin oblastı bütün həqiqi ədədlər çoxluğudur, çünki funksiya -in bütün qiymətləri üçün müəyyən edilmişdir. Qiymətlər çoxluğu a əmsalının işarəsindən asılıdır. Əgər olarsa, qiymətlər çoxluğu , əgər olarsa, olar.
Kvadrat funksiyanın qrafiki , və qiymətlərini dəyişdirməklə çevrilə bilər. Məsələn, müsbət sabitə vurulursa, qrafik şaquli olaraq uzanır və mənfi sabitə vurulursa, qrafik oxu ətrafında əks olunur. Əgər -a əlavə olunarsa və ya -dan çıxılırsa, qrafik üfüqi, isə -a əlavə edilirsə və ya ondan çıxarılırsa,
qrafik şaquli olaraq sürüşdürülür.

Modul (y=|x|) funksiyası və onun qrafiki
Mütləq qiymətin tərifinə görə
olduğundan aydındır ki, funksiyası bütün ədəd oxunda təyin olunub və mənfi olmayan qiymətlər alır.
-in qrafiki təpə nöqtəsi başlanğıcda olan V formalı əyridir. Əyrinin mailliyi -da dəyişir. Qrafik 1-ci və 2-ci rüblərin tənbölənidir. oxuna nəzərən simmetrikdir.
Məsələn , nöqtələri qrafik üzərində yerləşir və bu nöqtələr ordinat oxuna nəzərən simmetrikdir.

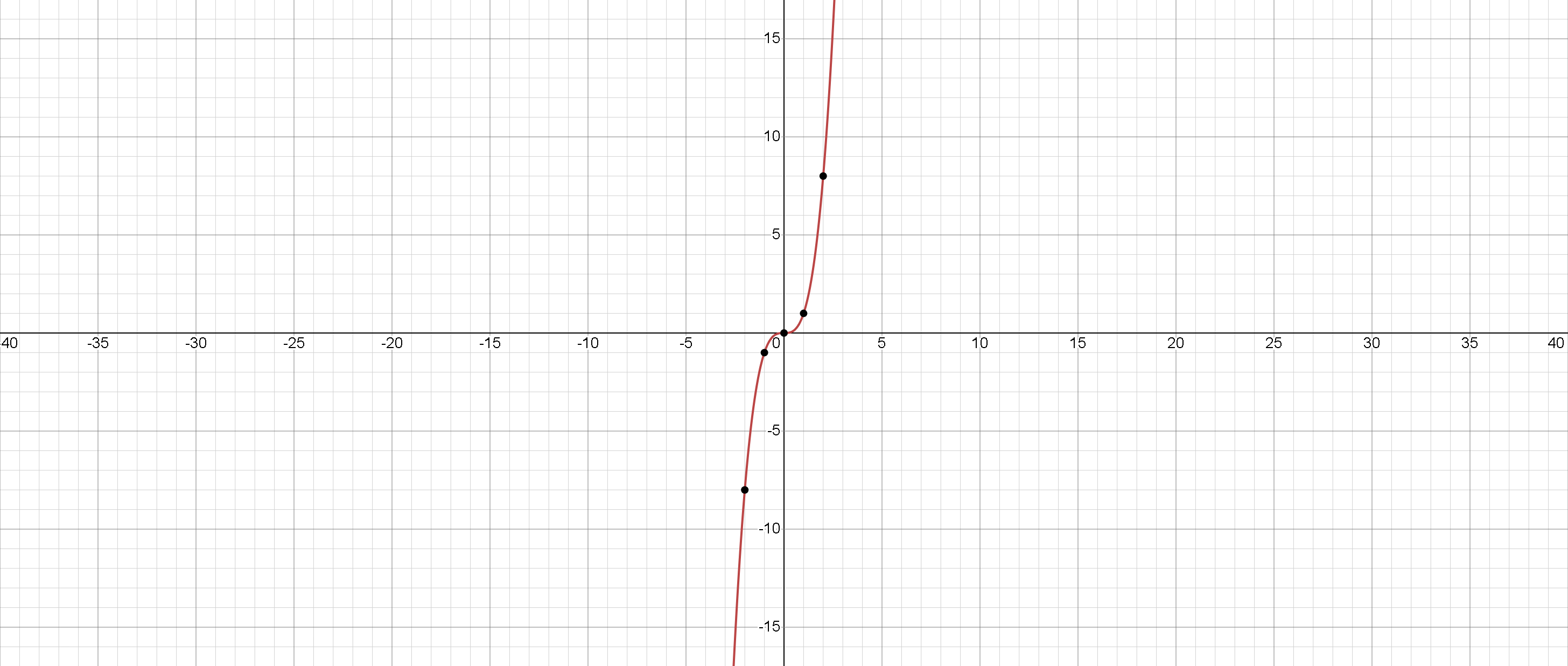
Kub funksiyası və onun qrafiki
funksiyası bütün ədəd oxunda təyin olunub və -in mənfi qiymətlərində mənfi, müsbət qiymətlərində isə müsbət qiymət alır. olduqda olur. Yəni, funksiyanın həm təyin oblastı, həm də qiymətlər çoxluğu bütün həqiqi ədədlərdir. funksiyasının qrafiki kub parabola adlanır. Koordinat başlanğıcından keçməklə 1-ci və 3-cü rüblərdə
yerləşir. funksiyası tək funksiyadır, bu o deməkdir ki, üçün . Bu xassə funksiyanın qrafikinin koordinat başlanğıcına nəzərən simmetrik olması ilə nəticələnir.