Yüksək dərəcəli tənliklər ☰

Sol tərəfi məchula nəzərən n dərəcəli çoxhədli, sağ tərəfi sıfır olan
\( a_n x^n+a_{n-1} x^{n-1}+⋯+a_1 x+a_0=0 \) şəklində tənliyə birdəyişənli \(n\) dərəcəli cəbri tənlik deyilir.
Burada \(a_n, a_{n-1}, …, a_1 ,a_0 \) əmsallar, \(n\) natural ədəd, \(a_n \neq 0\), \(x\) isə məchuldur.
Nümunə olaraq, \(2x^3–5x^2+3x–7=0\) tənliyi üçdərəcəli tənlikdir.
Üçdərəcəli və dörddərəcəli tənliklər üçün köklərin tapılması düsturları məlumdur, amma bu düsturlar çox mürəkkəbdir. Müəyyən hallarda, daha əlverişli olması üçün bu tənliklər müəyyən üsulların tətbiqi ilə həll edilir.

Vuruqlara ayırma üsulu.
Nümunə: \(x^3–x^2–4x+4=0\) tənliyini həll edək.
Vuruqlara ayırmaq üçün hədləri qruplaşdıraq.

\((x^3-x^2 )-(4x-4)=0\);

\(x^2 (x-1)-4(x-1)=0\);

\((x^2-4)(x-1)=0\);

\((x-2)(x+2)(x-1)=0\).

Hasilin sıfıra bərabər olması üçün vuruqlardan heç olmasa biri sıfır olmalıdır.
Bu halda \(x_1=2\), \(x_2=-2\), \(x_3=1\).


Başqa nümunəyə baxaq. \(x^3 –3x^2 +2x=0\).

\(x(x^2 -3x+2)=0\);

\(x(x-1)(x-2)=0\);

Bu halda \(x=0\), \(x=1\) və \(x=2\) olur.


Yeni dəyişən daxil etmə üsulu.
Yeni dəyişən daxil etməklə bir sıra tənlikləri kvadrat tənliklərə gətirmək mümkündür.
Məsələn, \(ax^{2n} +bx^n +c=0 \) tənliyi \(x^n=u\) əvəzləməsi ilə \(au^2 +bu+c=0\) tənliyinə gətirilir.
Xüsusi halda, \(n=2\) olduqda \(ax^4 +bx^2 +c=0 \) tənliyi \((a\neq 0)\) bikvadrat tənlik adlanır və onun həlli üçün \(x^2 =u\) əvəzləməsi aparılır.

Dörddərəcəli tənlik üçün nümunəyə baxaq.

\(x^4–5x^2+4=0\);

\((x^2 )^2-5x^2+4=0\);

\(u^2-5u+4=0\);

\((u-4)(u-1)=0\);

\(u-4=0, u=4\);

\(u-1=0, u=1\);

\(x^2=4; x^2=1\);

\(x=\pm 2\); \(x=\pm 1\).

Rasional tənliklər ☰

Tənliyin sağ və sol tərəfinə daxil olan ifadələr rasional ifadələr olarsa, belə tənliyə rasional tənlik deyilir.
Rasional tənliklər adətən aşağıdakı formada yazılır:

\( \frac{P(x)}{Q(x)} =\frac{R(x)}{S(x)} \)

burada \( Q(x) \neq 0 \), \( S(x)\neq 0 \) və \( P(x) \), \( Q(x) \), \( R(x) \) və \( S(x) \) çoxhədlilərdir.
Rasional tənliklərin həlli zamanı əsas məqsəd \(x\) dəyişəninin tənliyi doğru edən qiymətlərini tapmaqdır.
Rasional tənliyi həll etmək üçün ilk addım tənliyin hər iki tərəfini iki rasional ifadənin ortaq məxrəci ilə vuraraq məxrəclərdən azad olmaqdır. Bunu \(Q(x)\) və \(S(x)\) məxrəclərini vurmaqla və yaranan ifadəni sadələşdirməklə tapmaq olar.
Hər iki tərəfi ortaq məxrəcə vurduqdan sonra tənlik çoxhədli tənliyə çevrilir və onu standart cəbri üsullardan istifadə etməklə həll etmək olar. \(x\) üçün həllər tapıldıqdan sonra onların etibarlı həllər olduğuna əmin olmaq üçün onları orijinal tənlikdə yoxlamaq vacibdir. Həll bir və ya hər iki məxrəci sıfıra bərabər edirsə, bu etibarlı həll deyil və xaric edilməlidir.

Nümunə: \(\frac{1}{x+1} + \frac{1}{x-1} = \frac{10}{x^2-1} \).

Addım 1: Ortaq məxrəc tapılır.
İndiki halda ortaq məxrəc
\((x+1)(x-1)\).

Tənliyi aşağıdakı şəkildə yazaq və sadələşdirək:
\( \frac{1}{x+1} \cdot \frac{x-1}{x-1} + \frac{1}{x-1} \cdot \frac{x+1}{x+1} = \frac{10}{(x+1) \cdot (x-1)} \) ;

Sadələşdirək:
\(\frac{x-1}{(x+1)(x-1)} + \frac{x+1}{(x+1)(x-1)} = \frac{10}{(x+1)(x-1)} \) ;

Toplayaq:
\(\frac{2x}{(x+1)(x-1)} = \frac{10}{(x+1)(x-1)} \)

Addım 2: hər iki tərəfi ortaq məxrəcə vuraq: \(2x=10\).

Addım 3: \(x\) üçün həll edək. \(x = 5\).

Addım 4: Yoxlayaq. \(x=5\) tənliyin məxrəclərindən hər hansı biri \(0\) olmur.
Deməli, cavab, \(x=5\).

Modullu tənliklər ☰

Modullu tənliklər dəyişənin mütləq qiymətini ehtiva edən bir tənlik növüdür. Ədədin mütləq qiyməti ədəd oxunda sıfırdan məsafədir, ona görə də dəyişənin mütləq qiymətini dəyişənin ala biləcəyi sıfırdan məsafə kimi düşünmək olar.

Modullu tənliklərin həllinə əsas yanaşma tənliyi iki hala bölməkdir. Birinci hal, modul daxilindəki ifadə müsbət və ya sıfıra bərabərdir, digər hal isə modul daxilindəki ifadə mənfidir. Bunun səbəbi müsbət ədədin mütləq qiyməti ədədin özü olduğu halda, mənfi ədədin mütləq qiyməti onun əksidir.

Nümunələrə baxaq.
Tənliyi həll edin: \(|x-3|=5\).

İki hala baxaq:
Birinci hal: \(x-3\) müsbətdir.
\(x-3=5\).
\(x=8\).

İkinci hal: \(x-3\) mənfidir.
\(-(x-3)=5\).
\(-x+3=5\).
\(x=-2\).
Cavab: \(x=8\) və \(x=-2\).

Modullu tənliyin həlli olmaması da mümkündür.
Məsələn, tənliyi nəzərdən keçirək: \(|x-3|=-2\).
İstənilən ədədin mütləq qiyməti həmişə mənfi olmadığı üçün tənliyin sol tərəfini mənfi ədədə bərabər edən \(x\)-in heç bir dəyəri yoxdur. Buna görə də bu tənliyin həlli yoxdur.

İrrasional tənliklər ☰

Dəyişəni radikal işarəsi altında (və ya kəsr üstlü qüvvətə yüksəldilmiş) olan tənliklərə irrasional tənliklər deyilir.
Bu cür tənliklərin həlli adətən tənliyin bir tərəfində irrasional ifadənin təcrid olunmasını və sonra hər iki tərəfin qüvvətə yüksəldilməsini nəzərdə tutur ki, bu da radikalı aradan qaldıra bilər. Bununla belə, bu üsul orijinal tənliyi təmin etməyən həllər olan kənar həllər təqdim edə bilər. Bunun üçün də alınmış tənliyin köklərinin verilmiş tənliyi ödəyib ödəmədiyini yoxlamalıyıq. Həmçinin, tənliyin kökü olmaya da bilər.

Nümunə: \( \sqrt{x+1}-\sqrt{x-1}=1 \).
Bu tənliyi həll etmək üçün hər iki tərəfi 2-ci dərəcədən qüvvətə yüksəltməliyik:

\((\sqrt{x+1}-\sqrt{x-1})^2 = 1^2\)

\((x+1) - 2\sqrt{x+1} \cdot \sqrt{x-1} + (x-1) = 1 \)

\( 2\sqrt{x+1} \cdot \sqrt{x-1} = 2x-1 \)

\( (\sqrt{x+1} \cdot \sqrt{x-1})^2 = \left(\frac{2x-1}{2}\right)^2 \)

\( (x+1)(x-1) = \left(\frac{2x-1}{2}\right)^2 \)

\( x^2 - 1 = \frac{(2x-1)^2}{4} \)

\( 4x^2 - 4 = 4x^2 - 4x + 1 \)

\( -4x = -5 \)

\( x = \frac{5}{4} \)

Bununla belə, onun kənar olmadığına əmin olmaq üçün həllimizi yoxlamalıyıq.

İkidəyişənli tənliklər, tənliklər sistemi. ☰

İkidəyişənli tənliklər adətən x və y ilə işarələnən iki dəyişəni bərabərlik işarəsi ilə əlaqələndirən riyazi ifadələrdir. Tənliyi təmin edən x və y qiymətlərinə tənliyin həlli və ya kökləri deyilir. İkidəyişənli tənliyin sağ tərəfi sıfır, sol tərəfi standart şəkildə çoxhədli olarsa, bu çoxhədlinin dərəcəsi tənliyin dərəcəsi hesab edilir. İkidəyişənli tənliyin qrafiki, koordinatları tənliyin həlləri olan nöqtələr çoxluğudur.
Məsələn, \(y-4x=8\) tənliyinin qrafiki düz xətt, \(y=x^2-2x\) tənliyinin qrafiki paraboladır.
Bir neçə tənliyin hər birini ödəyən həlli tapmaq tələb olunduqda tənliklər fiqurlu mötərizənin köməyiylə birgə yazılır və onlara tənliklər sistemi deyilir. Sistemin tənliklərinin hər birinin həlli olan \((x; y)\) cütünə sistemin həlli, belə cütlər çoxluğuna isə sistemin həllər çoxluğu deyilir.

Bəzəkli mötərizədə tənliklər sisteminin yazılışı:
\( \begin{cases} \text{Birinci tənlik}\\ \text{İkinci tənlik} \end{cases} \)

Tənliklər sisteminin həlli üçün qrafik, əvəzetmə və tərəf-tərəfə toplama kimi müxtəlif üsullar mövcuddur. Seçdiyimiz üsul sistemin mürəkkəbliyindən asılıdır.
Tənliklər sistemini həll etməyin bir yolu qrafikdir. Qrafikləşdirmə bizə sistemin həllərini tənliklərin qrafiklərinin kəsişmə nöqtələri kimi vizuallaşdırmağa imkan verir. Tənliklərin qrafikini çəkmək üçün biz koordinat müstəvisində hər bir tənliyi təmin edən nöqtələri çəkirik, sonra xətləri yaratmaq üçün nöqtələri birləşdiririk. Xətlərin kəsişmə nöqtələri sistemin həllərini təmsil edir.

Nümunə: aşağıdakı tənliklər sistemini qrafik üsulla həll edək.
\( \begin{cases} y = 2x + 1 \\ y = -\frac{1}{3}x + 4 \end{cases} \)

Bu tənliklərin qrafikini çəkmək üçün biz \(x\)-in bir neçə dəyərini seçə və \(y\)-nin uyğun qiymətlərini tapmaq üçün onları hər bir tənliyə qoşa bilərik. Sonra ortaya çıxan nöqtələri çəkirik və xətləri yaratmaq üçün onları birləşdiririk.

Birinci tənlik üçün:

İkinci tənlik üçün:

İndi bu nöqtələri çəkə və xətlər yaratmaq üçün onları birləşdirə bilərik.
Alınan qrafik:
Xətlərin kəsişmə nöqtəsi təxminən \((1.3; 3.6)\) olan sistemin həllidir.

Başqa bir nümunədə əvəzetmə üsulundan istifadə edək:
\( \begin{cases} 2x + y = 4 \\ x - y = 1 \end{cases} \)

Burada \(x\) üçün: \(x=y+1\).
\(y\)-i \(x\)-lə əvəz edək: \(2(y+1)+y=4\).
Sadələşdirək və \(y\)-i tapaq: \(3y=2\) , \(y=\frac{2}{3}\).
Sonra \(x=y+1\) üçün \(y\)-in qiymətini yerinə yazıb \(x\)-i tapaq: \(x=\frac{2}{3} +1\), \(x=\frac{5}{3}\).
Tənliyin həlli: \( (\frac{5}{3}, \frac{2}{3}) \).

Bir tənliyi birdərəcəli, digəri ikidərəcəli olan tənliklər sistemi. ☰

Tənliklər sistemi bir qrup kimi birlikdə nəzərdən keçirilən tənliklər toplusudur. Bir tənliyin birinci dərəcəli (xətti), digərinin ikinci dərəcəli (kvadrat) olduğu tənliklər sistemi qeyri-xətti tənliklər sisteminin bir növüdür.
Sistemə daxil olan tənliklərin qrafiklərini eyni koordinat müstəvisində qurub, kəsişmə nöqtələrinin koordinatlarını tapmaqla sistemin həllərini (müəyyən dəqiqliklə) tapmaq olar. Qrafik üsulla həll sistemin həllərinin sayı haqqında fikir söyləmək üçün daha əlverişlidir. İkidəyişənli birdərəcəli tənliyin qrafiki olan düz xətlə ikidərəcəli tənliyin qrafikinin qarşılıqlı vəziyyətindən asılı olaraq tənliklər sisteminin həllər sayı müxtəlif ola bilər.
Məsələn:

• Düz xətt parabolanı iki nöqtədəd kəsir: sistemin iki həlli var.
• Düz xətt parabolanın toxunanıdır: sistemin bir həlli var.
• Düz xəttin parabola ilə ortaq nöqtəsi yoxdur: sistemin həlli yoxdur.

Bir tənliyin birinci dərəcəli, digərinin ikinci dərəcəli olduğu tənliklər sistemini həll etmək üçün bir neçə üsul var.

Bir nümunəyə baxaq.
\( \begin{cases} x + 2y = 3 \\ x^2 - 4y^2 = 0 \end{cases} \)

İkinci \( x^2 - 4y^2 \) tənliyini \( (x+2y)(x-2y)=0 \) şəklində yaza bilərik.
Bu da bizə iki mümkün hal verir: \( x+2y=0 \) və ya \( x-2y=0 \)
Burada birinci tənlikdən \( x+2y=0 \) olmadığını görə bilirik, bunun üçün də sistemdəki birinci tənlik üçün \( x=2y \) əvəzləməsini aparırıq:
\( 2y+2y=3 \)
\( 4y=3 \)
\( y = \frac{3}{4} \)
Sonra \( x=2y\)-də \(x = \frac{3}{2} \) əvəzləməsi ilə \(y\)-i tapaq.
Tənliyin həlli: \( (x,y)=(\frac{3}{2}, \frac{3}{4}) \).

Hər iki tənliyi ikidərəcəli olan tənliklər sistemi ☰

Bu tip sistem qeyri-xəttidir, yəni sistemin həlləri mütləq düz xətt təşkil etmir. Bunun əvəzinə, həllər \(xy\) müstəvisində əyrilər və ya diskret nöqtələr dəsti ola bilər.
Sistemin həlli hər iki tənliyi eyni vaxtda təmin edən \(x\) və \(y\) qiymətləri olacaqdır. Sistemdəki xüsusi tənliklərdən asılı olaraq, bir və ya bir neçə həll yolu ola bilər, ya da sistemin həlli olmaya bilər.
\(xy\)-müstəvisində tənliklərin qrafiki mümkün həllərin vizual təsvirini təmin edə bilər və sistemin davranışını başa düşməyə kömək edə bilər.

Məsələn:
\( \begin{cases} x^2+y^2=25 \\ x^2-y^2=9 \end{cases} \)

Bu sistem, radiusu 5 olan başlanğıcda mərkəzi olan dairə ilə şaquli oxu olan və başlanğıcda mərkəzləşmiş hiperbolanın kəsişməsini təmsil edir.

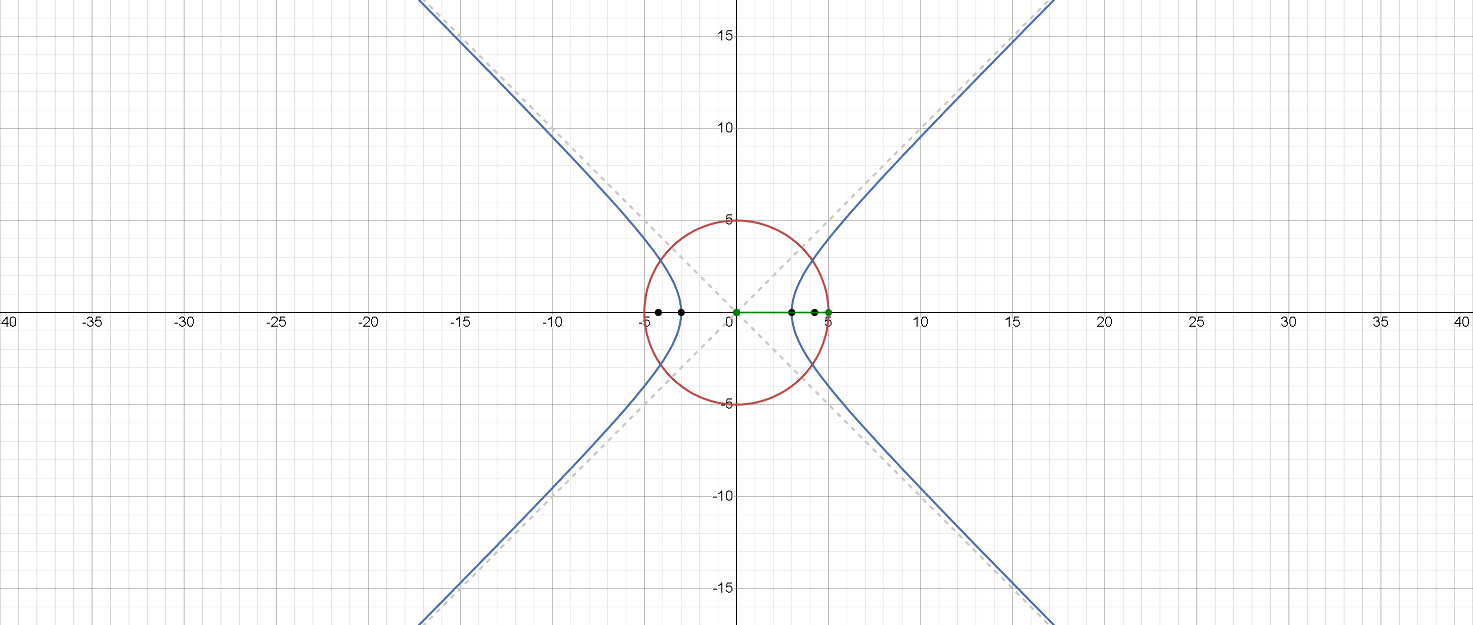
Bu qrafiklə sistemin dörd həlli olduğunu deyə bilərik.
İki tənliyi tərəf-tərəfə toplamaqla həll edək:
\( \begin{cases} x^2+y^2=25 \\ +\\ x^2-y^2=9 \end{cases} \)

\(2x^2 = 34\)

\( x^2 = 17 \).

Hər iki tərəfin kvadrat kökünü götürsək, \( x = \pm \sqrt{17} \) alırıq. Bu dəyərləri yenidən orijinal tənliklərdən birinə əvəz etməklə, \(y\) üçün həll edə bilərik.
Məsələn, birinci tənliyi istifadə edərək, əldə edirik:
\( (\sqrt{17})^2 + y^2 = 25 \)

\( y^2 = 8 \)

\( y = \pm 2 \sqrt{2} \)


Bu halda tənliyin həlli:

\( (\sqrt{17}, 2 \sqrt{2}) \),

\( (\sqrt{17}, -2 \sqrt{2}) \),

\( (-\sqrt{17}, 2 \sqrt{2}) \)

\( (-\sqrt{17}, -2 \sqrt{2}) \).