Vektorlar
Bir çox kəmiyyətlər, kütlə, uzunluq, zaman, temperatur və s. yalnız ədədi qiyməti ilə xarakterizə edilir. Bu cür kəmiyyətlər
skalyar kəmiyyətlər
adlanır. Bəzi kəmiyyətlər isə, məsələn, yerdəyişmə, sürət, təcil, qüvvə və s. təkcə ədədi qiyməti ilə deyil, həm də istiqaməti ilə müəyyən edilir. Bu cür kəmiyyətlər
vektorial kəmiyyətlər
adlanır. Yerdəyişmə vektorial kəmiyyətlərə ən sadə nümunədir. Cismin A nöqtəsindən B nöqtəsinə yerdəyişməsi A-dan B-yə doğru yönəlmiş parça ilə -vektola göstərilir.
Vektor
İstiqamətlənmiş düz xətt parçası ilə təsvir olunur. Vektoru göstərən parçanın uzunluğuna
vektorun uzunluğu və ya modulu
deyilir.
Vektor başlanğıc və son nöqtəsi adlandırılmaqla işarə edilir. Məsələn, \(\overrightarrow{AB}\) vektoru, burada A vektorun başlanğıc, B isə son nöqtəsidir.
Vektor kiçik hərflərlə də işarə edilir, məsələn \(\overrightarrow{u} \) vektoru. \(\overrightarrow{u}\) vektorunun uzunluğu \( |\overrightarrow{u}| \) kimi işarə olunur.
Başlanğıc və son nöqtələri üst-üstə düşən vektor
sıfır vektor
adlanır və \( \overrightarrow{0} \) işarə edilir. Sıfır vektorunun uzunluğu sıfıra bərabərdir, istiqaməti isə qeyri-müəyyəndir.
Bir düz xətt üzərində və ya paralel düz xətlər üzərində yerləşən vektorlara
kollinear vektorlar
deyilir.
Kollinear vektorlar eyni istiqamətli və ya əks istiqamətli vektorlardır. Vektorların eyni istiqamətli olması \( \overrightarrow{u} \upuparrows \overrightarrow{v} \) kimi, əks istiqamətli olması isə \( \overrightarrow{u} \uparrow \downarrow \overrightarrow{v} \) kimi yazılır.
İki vektorun istiqamətləri eyni, uzunluqları bərabər olarsa, bu vektorlar
bərabər vektorlar
adlanır. \( \overrightarrow{u} = \overrightarrow{v} \) kimi yazılır.
İki vektorun istiqamətləri əks, uzunluqları bərabər olarsa, bu vektorlar
əks vektorlar
adlanır. \( \overrightarrow{|u|} = \overrightarrow{|v|} \) və ya \( \overrightarrow{u} = -\overrightarrow{v} \) kimi yazılır.
Vektorun uzunluğu
Koordinat müstəvisi üzərində vektor \( \vec{AB} = \langle a; b \rangle \) kimi yazılır. \( \langle a; b \rangle \) yazılışı vektorun komponentlərlə yazılışıdır. Vektor komponentləri bir vektor kəmiyyətini daha çox riyazi təcrübəyə malik olduğumuz iki (və ya daha çox) skalyar kəmiyyətə bölməyə imkan verir. Vektor komponentləri vektor cəbrində vektorları toplamaq,
çıxmaq və vurmaq üçün istifadə olunur. Bir vektorun digəri boyunca komponenti birinci vektorun ikinci vektor istiqamətində uzanan hissəsidir. Bərabər vektorların uyğun komponentləri bərabərdir. Tərsinə, vektorların uyğun komponentləri bərabərdirsə, onda vektorlar bərabərdir.
Hər hansı \( \overrightarrow{AB} \) vektoru verildikdə başlanğıc müstəvinin istənilən nöqtəsində olmaqla bu vektora bərabər bir vektor qurmaq olar. Deməli, fərqli başlanğıc nöqtələri seçməklə verilən vektora bərabər sonsuz sayda vektor qurula bilər. Başlanğıc nöqtəsi \( A(x_1;y_1 ) \), son nöqtəsi isə \( B(x_2;y_2 ) \) olan \( \vec{AB} = \langle a; b \rangle \)
vektorunu bu nöqtələrin koordinatlarına görə komponentləri ilə ifadə etmək olar.
\( x_2 - x_1 =a \), \( y_2 - y_1 = b \) olduğundan \( \vec{AB} = \langle x_2 - x_1; y_2 - y_1 \rangle = \langle a; b \rangle \) alarıq. \( \langle a; b \rangle \) vektorunu koordinat başlanğıcından ayırdıqda sonu \( (a;b) \) nöqtəsində yerləşir. \(a\) və \(b\) ədədlərinə \( \langle a; b \rangle \) vektorunun koordinatları da deyilir.
Vektorun uzunluğunu
başlanğıc və son nöqtələrin koordinatlarına görə iki nöqtə arasındakı məsafə düsturundan istifadə etməklə tapmaq olar.
\( |\vec{AB}| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Üç ölçülü fəzada isə $$ |\vec{AB}| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$
\( \vec{AB} = \langle a; b \rangle \) vektorunun uzunluğu \( \vec{|AB|}= \sqrt{a^2+b^2} \) düsturu ilə hesablanır.
Vektorun istiqaməti. Meyil bucağı.
Koordinat başlanğıcından ayrılmış vektoru onun uzunluğu və absis oxu ilə əmələ gətirdiyi bucaqla vermək olar. Vektorun istiqamətini absis oxunun müsbət istiqamətindən saat əqrəbinin hərəkətinə əks olmaqla ölçülən bucaqla müəyyən edib, ona vektorun meyil bucağı deyəcəyik.
Komponentləri \( (v_x,v_y ) \) olan, meyl bucağı \( \theta \) ilə işarələnən \( \vec{v} \) vektoru üçün:
Vektorun uzunluğu: \( \vec{|v|} = \sqrt{v_x^2 + v_y^2} \)
Vektorun meyil bucağı: \( \tan\theta = \frac{v_y}{v_x} \) və ya \( \cos\theta = \frac{v_x}{|v|} \)
Hər hansı vektorun meyil bucağı koordinat başlanğıcından verilmiş vektora bərabər vektor ayırmaqla tapılır. Qeyd edək ki, meyil bucağı vektorun başlanğıc nöqtəsindən absis oxuna paralel üfüqi ox keçirməklə də tapıla bilər.
Koordinat müstəvisində verilmiş \( \vec{v} \) vektorunun komponentlərlə \( \vec{v} = \langle v_x ; v_y \rangle \) yazılışını triqonometrik nisbətlərin köməyi ilə ifadə edək.
\( cos \theta = \frac{v_x}{\vec{|v|}} \),
\( sin \theta = \frac{v_y}{\vec{|v|}} \),
\( v_x = \vec{|v|} \cos\theta \),
\( v_y = \vec{|v|} \sin\theta \)
düsturlarını nəzərə alaraq \( \vec{v} \) vektorunu
\( \mathbf{v} = \langle \vec{|v|} \cos(\theta); \vec{|v|} \sin(\theta) \rangle \)
şəklində komponentləri ilə ifadə etmək olar.
Kollinear vektorların toplanması və çıxılması
Kollinear \( \vec{u} \) və \( \vec{v} \) vektorlarını toplamaq üçün \( \vec{v} \) vektorunu elə yerləşdirin ki, onun başlanğıcı \( \vec{u} \) vektorunun sonu ilə üst-üstə düşsün. u vektorunun başlanğıcından v vektorunun sonuna yönəlmiş vektor u və v vektorlarının cəmini göstərib onların əvəzləyicisi olur.
Eyni istiqamətli kollinear vektorların cəmini göstərən əvəzləyici vektorun modulu verilən vektorların modulları cəminə bərabər olmaqla, istiqaməti verilən vektorla eyni olur.
Əksistiqamətli iki kollinear vektorun əvəzləyici vektorunun modulu bu vektorların modulları fərqinə bərabərdir (böyük moduldan kiçiyi çıxılır), istiqaməti isə modulu böyük olan vektorla eynidir.
Ümumiləşdirsək u və v vektorları əks istiqamətli vektorlardırsa, əvəzləyici r vektoru:
- \( \vec{|u|} > \vec{|v|} \) olarsa, \( \vec{|r|} = \vec{|u|} - \vec{|v|} \), r vektoru u vektoru ilə eyni istiqamətdə olur.
- \( \vec{|u|} < \vec{|v|} \) olarsa, \( \vec{|r|}=\vec{|v|} - \vec{|u|} \), r vektoru v vektoru ilə eyni istiqamətdə olur.
- \( \vec{|u|} = \vec{|v|} \) olarsa, \( \vec{|r|} = 0 \), yəni, əks vektorların cəmi \( \vec{0} \) vektoruna bərabərdir.
\(u-v\) fərqini tapmaq üçün \(u\)-nun üzərinə \(v\)-yə əks olan vektoru əlavə etmək lazımdır. Yəni, \(u - v\) ifadəsi ilə \(u + (-v) \) ifadəsi ekvivalentdir.
Kollinear olmayan vektorların toplanması və çıxılması
Qeyri-kollinear vektorlar eyni xətt üzərində olmayan vektorlardır. Qeyri-kollinear vektorları topladıqda və ya çıxdıqda, vəziyyətdən asılı olaraq paraleloqram və ya üçbucaq qaydasından istifadə edirik.
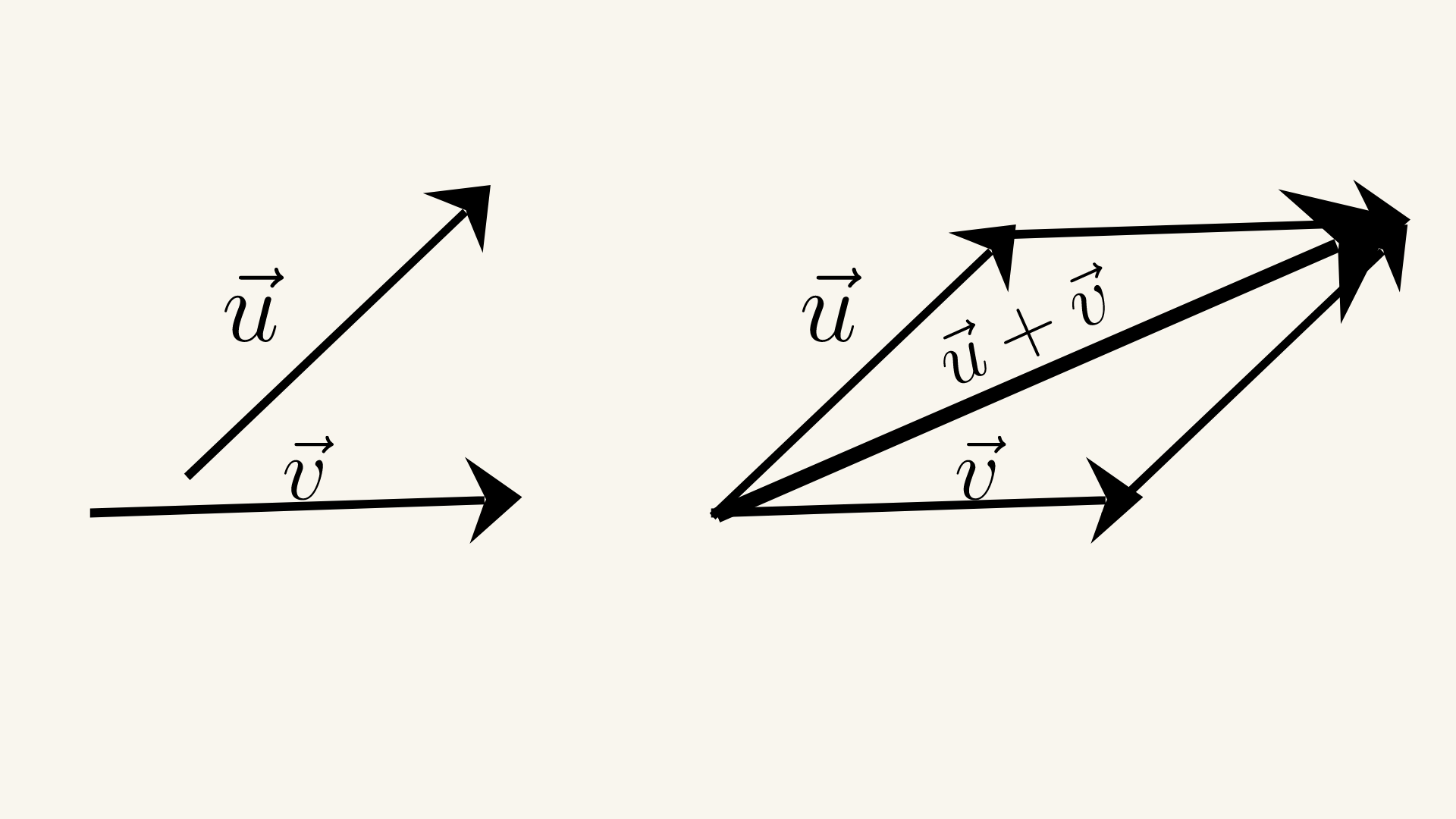
Paraleloqram qaydası
1. verilir u və v vektorları.
2. v vektorunu elə sürüşdürək ki u və v vektorlarının başlanğıc nöqtələri üst-üstə düşsün.
3. u və v vektorlarını uyğun olaraq paralel köçürmə ilə tərəfləri u və v olan paraleloqram quraq. Bu paraleloqramın u və v vektorlarının başlanğıc nöqtəsindən çıxan diaqonalı onların cəmini, u+v vektorunu göstərir.
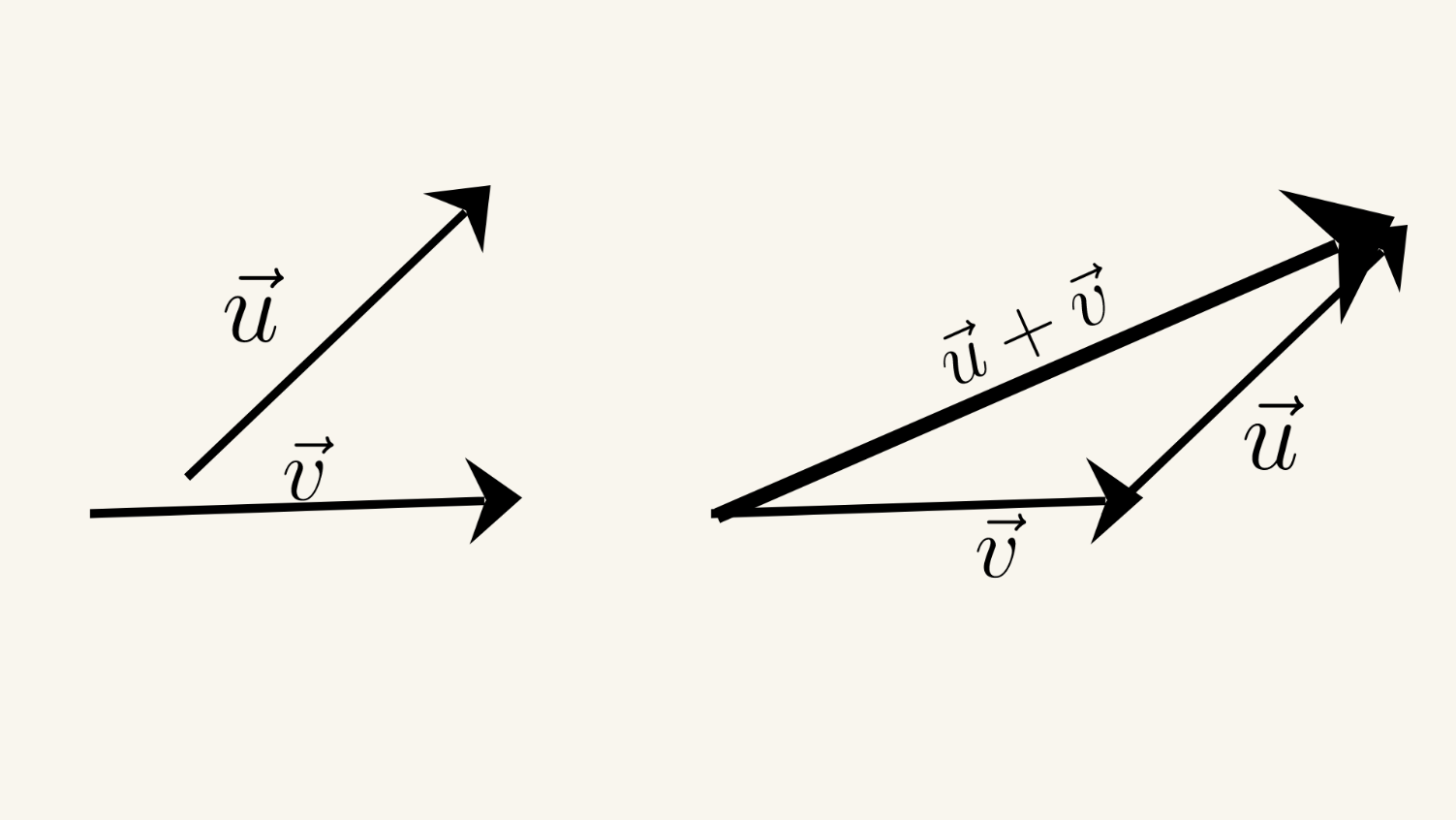
Üçbucaq qaydası
1. verilir u və v vektorları.
2. u vektorunu elə yerləşdirək ki, v vektorunun son nöqtəsi ilə u vektorunun başlanğıc nöqtəsi üst-üstə düşsün.
3. v vektorunun başlanğıc nöqtəsi ilə u vektorunun son nöqtəsini birləşdirən istiqamətlənmiş parça v+u vektorunu ifadə edən əvəzləyici vektordur.
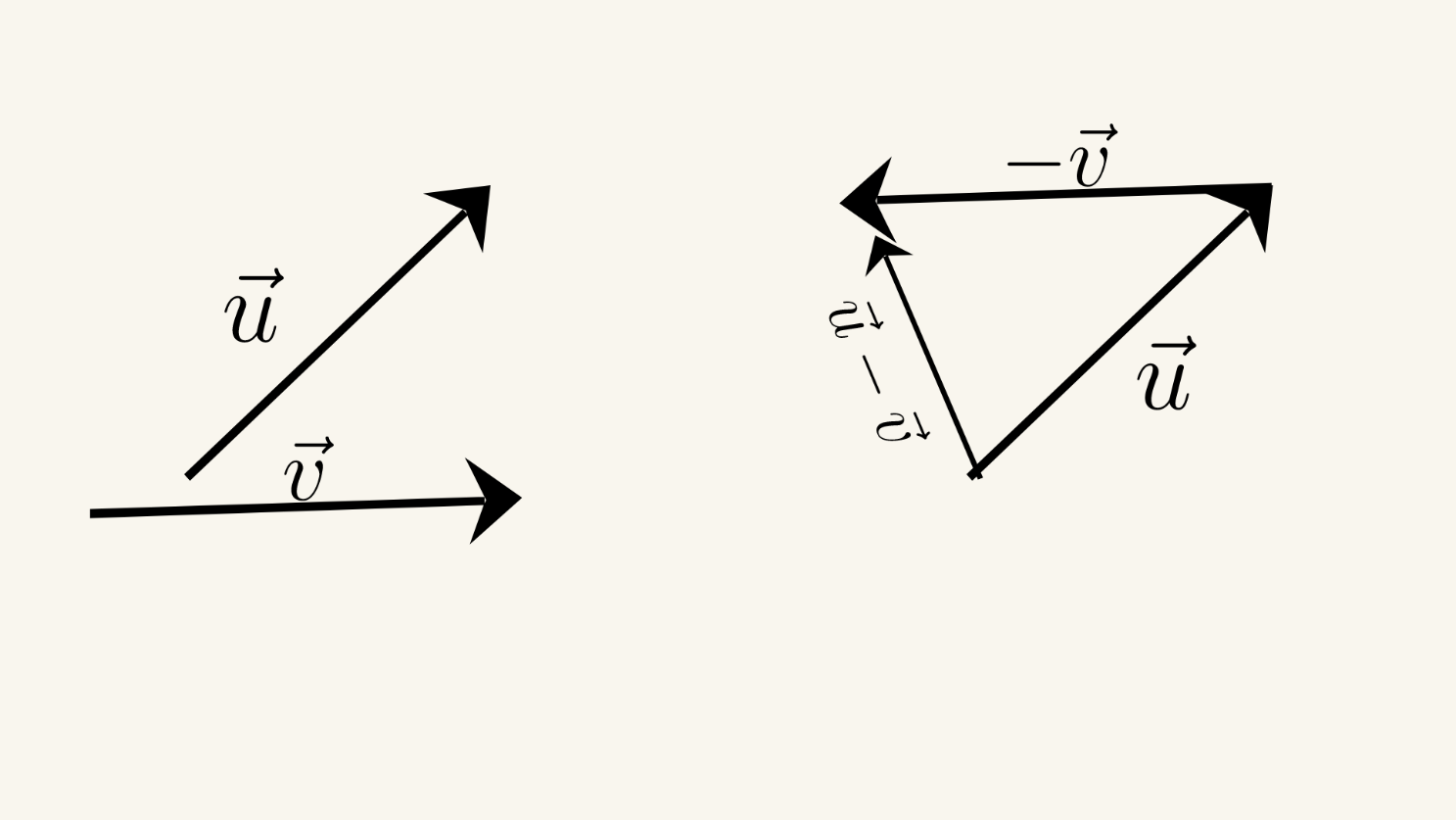
Vektorların çıxılması:
Qrafik qayda ilə u-v vektorunu müəyyən edək.
1. v vektoruna əks vektoru (-v) çəkək.
2. -v-ni elə sürüşdürək ki, -v vektorunun başlanğıc nöqtəsi ilə u vektorunun son nöqtəsi üst-üstə düşsün.
3. u vektorunun başlanğıc nöqtəsi ilə -v vektorunun son nöqtəsini birləşdirən istiqamətlənmiş parça u-v vektorudur.
Vektorların toplanmasının xassələri.
İstənilən u, v, və z vektorları üçün toplamanın aşağıdakı xassələri doğrudur :
- Yerdəyişmə xassəsi: u+v=v+u.
- Qruplaşdırma xassəsi: (u+v )+z=u+(v+z ).
- İdentiklik xassəsi: u+0=u.
- Əks vektorların cəmi: u+(-u )=0
Vektorların komponentlərindən istifadə etməklə toplanması
Dekart koordinat müstəvisi üzərində komponentləri ilə verilmiş vektorların toplanması qaydası.
\( \vec{u} = \langle a_1 ; b_1 \rangle \) və \( \vec{u} = \langle a_2 ; b_2 \rangle \) vektorlarının cəmi \( \vec{u} + \vec{v} = \langle a_1 + a_2 ; b_1 + b_2 \rangle \) vektorudur.
Komponentlərdən istifadə edərək vektor əlavə edərkən ilk addım hər bir vektoru \(x\) və \(y\) komponentlərinə bölməkdir. Bu, sinus və kosinus kimi triqonometrik funksiyalardan istifadə etməklə edilə bilər. Məsələn, \(x\) oxuna münasibətdə böyüklüyü “\(r\)” və bucağı "\(\theta \)" olan vektor verildikdə onun \(x\) və \(y\) komponentləri aşağıdakı kimi tapıla bilər:
\(x\)-komponent: \(r\cdot cos(\theta) \).
\(y\)-komponent: \(r\cdot sin(\theta) \).
Hər iki vektor \(x\) və \(y\) komponentlərinə bölündükdən sonra komponentlər ayrıca toplana bilər.
Məsələn, iki A və B vektorumuz varsa, onların \(x\)-komponentləri bir yerdə toplanmalıdır ki, nəticədə C vektorunun \(x\)-komponenti, \(y\) komponentləri bir yerdə toplanmalıdır ki, C vektorunun \(y\)-komponenti əldə olunsun:
\(C_x = A_x+ B_x \)
\(C_y= A_y+ B_y \)
Nəhayət, C vektorunun böyüklüyü və bucağı müvafiq olaraq Pifaqor teoremindən və tərs triqonometrik funksiyalardan istifadə etməklə tapıla bilər:
C vektorunun böyüklüyü: \( \sqrt{C_x^2 + C_y^2} \) .
C vektorunun bucağı: \( tg^{-1}(\frac{C_y}{C_x}) \) .
Qeyd edək ki, C-nin bucağını onun hansı kvadrantda olduğuna görə tənzimləmək lazım gələ bilər, çünki tərs triqonometrik funksiyalar yalnız \( -\frac{\pi}{2} \) ilə \( \frac{\pi}{2} \) diapazonunda bucaqlar verir.
Vektorun ədədə vurulması
\( \vec{u} \) vektorunun \(k\) ədədinə \( (k \in R) \) hasili \( k \cdot \vec{u} \) kimi işarə edilir və bu vektorun uzunluğu \( |k| \cdot \vec{|u|} \)-ya bərabərdir.
\( k > 0 \), olarsa ku vektoru u vektoru ilə eyni istiqamətli olur.
\( k < 0 \), olarsa ku vektoru u vektoru ilə əks istiqamətli olur.
Verilən vektorla onun (sıfırdan fərqli) ədədə hasilini ifadə edən vektor kollineardır.
\( \vec{u} \neq 0 \) və \( v \) vektorları kollineardırsa, onda elə yeganə k ədədi var ki, \( \vec{v} = k \cdot \vec{u} \) olur.
-
İstənilən \(k\) və \(l\) ədədləri \( (k,l \ in R) \) və \( \vec{v} \) vektoru üçün:
\( (k+l) \vec{v} = k \vec{v} + l \vec{v} \). -
İstənilən \(k\) ədədi \( (k \in R) \) və istənilən \( \vec{u} \) və \( \vec{v} \) vektorları üçün:
\( k( \vec{u} + \vec{v}) = k \vec{u} + k \vec{v} \). -
İstənilən \(k\) və \(l\) \( (k, l \in R) \) ədədləri və \( \vec{v} \) vektoru üçün:
\( (kl) \vec{v} = k (l \vec{v}) \).
Skalyar vurma vektorların xətti birləşmələrini tapmaq üçün də istifadə edilə bilər. İki vektorun xətti birləşməsi sadəcə olaraq vektorların skalyar əmsallara vurulan cəmidir.
Məsələn, \( \vec{v} = (2, 3) \) və \( \vec{w} = (1, -1) \) iki vektoru verildikdə, \( 3 \vec{v} - 2 \vec{w} \) xətti kombinasiyası aşağıdakı kimi hesablana bilər:
$$ \begin{align*} &3\vec{v} = 3(2,3) = (6,9)& \\ &2\vec{w} = 2(1,-1) = (2,-2)& \\ &3\vec{v} - 2\vec{w} = (6,9) - (2,-2) = (4,11)& \end{align*} $$
Paralel köçürmə
Paralel köçürmədə nöqtələr paralel (yaxud üst-üstə düşən) düz xətlər üzrə eyni məsafə qədər yerini dəyişir və fiqur özünə konqruyent fiqura çevrilir.
Fiqurun paralel köçürülməsində ixtiyari \(A(x;y)\) nöqtəsi \(A^` (x^`;y^`) \) nöqtəsinə çevrilir və nöqtələrin koordinatları arasında \(x^`=x+a \), \( y^`=y+b \) bərabərlikləri doğrudur.
Koordinat müstəvisi üzərində paralel köçürmədə koordinat oxları boyu sağa və yuxarı yerdəyişmə müsbət, sola və aşağı yerdəyişmə isə mənfi \(a\) və \(b\) ədədləri ilə təyin olunur. Paralel köçürmədə iki nöqtə arasındakı məsafə dəyişmir.
Paralel köçürmədə ixtiyari iki \( A(x_1; y_1 ) \) və \( B(x_2; y_2 )\) nöqtələri uyğun olaraq \(A^` (x_1+a; y_1+b ) \) və \( B^` (x_2+a;y_2+b ) \) nöqtələrinə çevrilirsə, alırıq:
\( AB = \sqrt{(x_2 - x_1)^2 + (y_2 + y_1)^2} \)
$$ A^` B^` = \sqrt{((x_2 + a) - (x_1 + a))^2 + ((y_2 + b) - (y_1 + b))^2} $$
Buradan \( AB=A^` B^` \). Deməli paralel köçürmədə məsafə saxlanılır.
\( AB^` \) parçasının orta nöqtəsinin koordinatları
\( x_0 = \frac{x_1 + x_2 +a}{2} \) , \( y_0 = \frac{y_1 + y_2 +b}{2} \) kimi tapılır.
Paralel köçürmədə düz xətt paralel düz xəttə (və ya özünə) çevrilir.
Bir fiqurun digərinə çevrilməsində nöqtələr arasındakı məsafə saxlanarsa, bu çevrilməyə
hərəkət
deyilir. Paralel köçürmə hərəkətdir.
Hər bir paralel köçürmə bir vektor müəyyən edir. Yəni, paralel köçürmədə fiqurun bütün nöqtələrinin yerdəyişməsi bir vektor üzrə icra edilir.
Hərəkət və konqruyent fiqurlar
Fiqurların çevrilməsində nöqtələr arasındkı məsafə saxlanarsa, fiqurun bütün həndəsi xassələri saxlanılır və fiqur özünə konqruyent fiqura çevrilir. Belə çevrilmələrə hərəkət deyilir. İki ardıcıl hərəkətin nəticəsi də hərəkətdir. Hərəkətdə parça parçaya çevrilir. Düz xəttə nəzərən simmetriya çevrilməsi (əksetmə) hərəkətdir. Konqruent fiqurlar eyni ölçü və formaya malik olan, onlara uyğun tərəfləri və bucaqları uyğun olan həndəsi fiqurlardır. Yəni, əgər iki fiqur konqruyentdirsə, onların uyğun tərəfləri, bucaqları və təpələri konqruentdir.