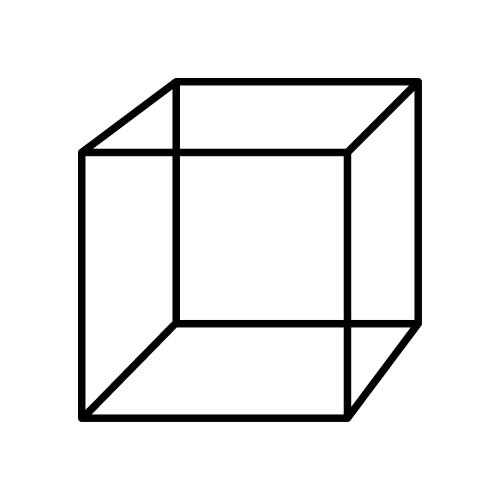
Kub ☰

Həcm düsturu:

\(V=a^3\)

Kubun səthinin sahəsi:

\(S=6a^2\)

Kubun yan səthinin sahəsi:

\(S=4a^2\)

Diaqonalı:

\(d= a \sqrt{3}\)

Tərifi:

Ölçüləri bərabər olan düzbucaqlı paralelepipedə Kub deyilir. Üzlərin sayı 6, forması kvadrat, tillərin sayı 12, təpə nöqtələrin sayı 8, bir nöqtədən çıxan tillərin sayı 3-dür.

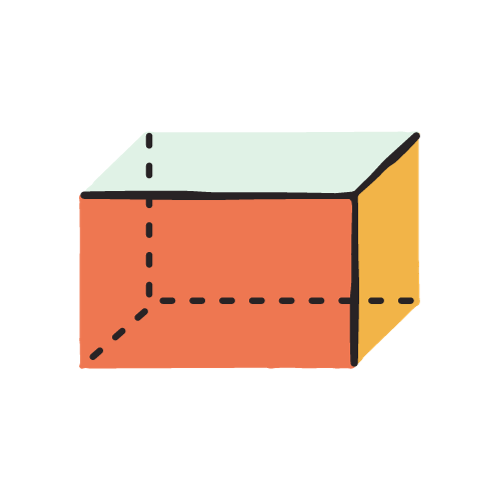
Paralelepiped ☰

Düzbucaqlı paralelepipedin həcm düsturu:

\(V=a \cdot b \cdot c \)

Tam səthinin sahəsi:

\( \small S_\text{tam} = 2 \cdot ( a \cdot b + a \cdot c + b \cdot c) \)

Yan səthinin sahəsi:

\(S_\text{yan} = 2 \cdot ( a \cdot c + b \cdot c ) \)

Diaqonalları:

\( d^2 = a^2 + b^2 + c^2 \)

\(a\) və \(b\) oturacağın tərəfləri, \(c\) paralelepipedin tili, \(d\) isə diaqonalıdır.

Tərifi:

Düzbucaqlı paralelepiped – Oturacağı düzbucaqlı olan düz paralelepipede düzbucaqlı paralelepiped deyilir.12 tili vardır və bir təpədən çıxan tillərinə onun ölçüləri deyilir. Bu ölçülər eni uzunluğu və hündürlüyüdür. Teorem: düzbucaqlı paralelepipedin dioqanılının kvadratı onun bir təpədən çıxan tillərinin(üç ölçüsünün) kvadratları cəminə bərabərdir.

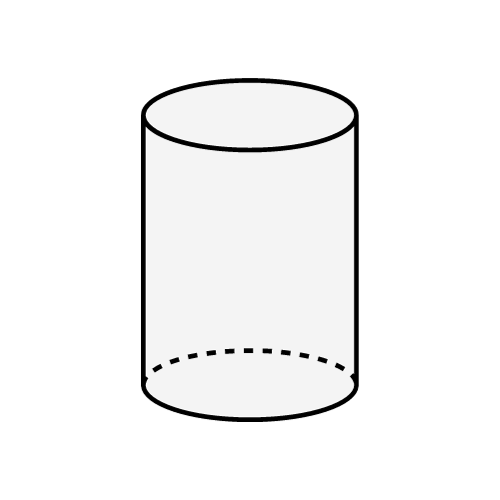
Silindr ☰

Həcm düsturu:

\(V= \pi r^2 \cdot h\)

Tam səthinin sahəsi:

\( \small S_\text{tam} = 2 \pi r \cdot h + 2 \cdot \pi r^2 = 2 \pi r(r+h) \)

Yan səthinin sahəsi:

\(S_\text{yan} = 2 \pi r \cdot h \)

Ox kəsiyinin sahəsi:

\(S_\text{ox} = 2RH \)

Tərifi:

Düzbucaqlının hər hansı tərəfi ətrafında fırlanmasından alınan cisim silindr adlanır.

Prizma ☰

Həcm düsturu:

\(V= S_\text{ot} \cdot h \)

Tam səthinin sahəsi:

\( \small S_\text{tam} = 2 S_\text{ot} + S_\text{yan} \)

Yan səthinin sahəsi:

\(S_\text{yan} = P_\text{ot} \cdot l \)

\( S_\text{ot} \) oturacağın sahəsi
\( p_\text{ot} \) oturacağın perimetri
\(l\) yan üzün maili hündürlüyü.

Tərifi:

Üzləri düz olan üçölçülü həndəsi fiqurdur. Prizmalar düzbucaqlı üzlər dəsti ilə birləşdirilən, oturacaqlar adlanan iki uyğun, paralel çoxbucaqlı üz ilə xarakterizə olunur. İki üzü (oturacaqları) ixtiyari bərabər çoxbucaqlıdır. Yan üzləri oturacaq müstəvisinə perpendikulyar olan prizma düz prizma, Yan üzləri oturacaq müstəvisinə maili olan prizma mail prizma adlanır.
Oturacağı düzgün çoxbucaqlı olan düz prizma düzgün prizma adlanır. Prizmanın həcmi oturacağının sahəsi ilə hündürlüyü (oturacaqlar arasındakı məsafə) hasilinə bərabərdir

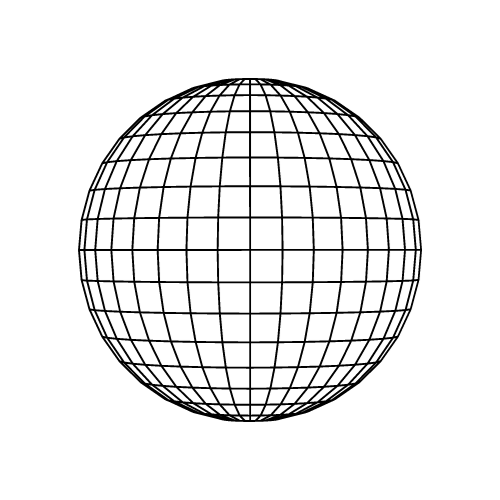
Kürə ☰

Həcm düsturu:

\( V = \frac{4}{3} \pi r^3 \)

Səthinin sahəsi:

\( S = 4 \pi r^2 \)

Diameteri:

\( D=2r \)

Tərifi:

Kürə, səthindəki bütün nöqtələri mərkəz adlanan sabit bir nöqtədən bərabər məsafədə olan mükəmməl simmetrik fırlanma fiqurudur. Mərkəzlə kürənin istənilən nöqtəsi arasındakı məsafəyə radius deyilir. Kürələrin sonsuz simmetriya xətləri və ən böyük həcm-səth nisbəti var ki, bu da onları istilik itkisini və ya buxarlanmanı minimuma endirmək üçün ideal edir.
Kürə səthinin istənilən iki nöqtəsini birləşdirən düz xətt parçasına kürənin vətəri, mərkəzdən keçən vətərə isə kürənin diametri deyilir.