Vectores ☰

Los vectores son objetos matemáticos que se utilizan comúnmente en varios campos de la ciencia, la ingeniería y las matemáticas. Se usan para representar cantidades físicas como fuerza, velocidad, aceleración y desplazamiento que tienen tanto magnitud como dirección.
Un vector suele representarse por una flecha con una longitud y una dirección. La longitud de la flecha representa la magnitud del vector, mientras que la dirección de la flecha representa la dirección del vector. La magnitud de un vector es un valor escalar y se denota por \(|\vec{v}|\).
Los vectores pueden ser denotados nombrando sus puntos de inicio y fin, donde el punto de inicio es la cola del vector y el punto final es la cabeza del vector. Por ejemplo, el vector desde el punto \(A\) hasta el punto \(B\) se puede denotar como \(\overrightarrow{AB}\).

Los vectores tienen varias propiedades importantes en matemáticas y física. Algunas de las propiedades clave de los vectores incluyen:

Magnitud: Los vectores tienen una magnitud o longitud, que es un escalar no negativo que representa el tamaño del vector.

Dirección: Los vectores tienen una dirección, que puede ser especificada usando ángulos u otras notaciones direccionales. La dirección de un vector se define por el ángulo entre el vector y una dirección de referencia fija.

Adición: Los vectores pueden ser sumados utilizando la ley del paralelogramo o la ley del triángulo de adición de vectores. Esto implica sumar las componentes correspondientes de cada vector para obtener el vector resultante.

Multiplicación escalar: Los vectores pueden ser multiplicados por escalares, lo que cambia la magnitud y/o dirección del vector. La multiplicación escalar implica multiplicar cada componente del vector por un escalar.

Producto punto: Los vectores pueden ser multiplicados juntos utilizando el producto punto o producto escalar. El producto punto de dos vectores es un escalar que representa el producto de sus magnitudes y el coseno del ángulo entre ellos.

Producto cruz: Los vectores también pueden ser multiplicados utilizando el producto cruz o producto vectorial. El producto cruz de dos vectores es un vector que es perpendicular a ambos vectores de entrada y tiene una magnitud igual al producto de sus magnitudes por el seno del ángulo entre ellos.

Vector cero: Existe un vector único llamado vector cero, denotado por \(\vec{0}\), que tiene una magnitud de \(0\) y no tiene dirección. Se puede pensar en él como el vector que va de un punto a sí mismo, o equivalentemente, como la diferencia entre dos vectores iguales.
Por ejemplo, \(\overrightarrow{OA} - \overrightarrow{OA} = 0\).

Vector unitario: Un vector unitario es un vector con una magnitud de 1. Cualquier vector no nulo se puede dividir por su magnitud para obtener un vector unitario en la misma dirección.

Vectores colineales: Los vectores son colineales si están en la misma línea o son paralelos. En otras palabras, tienen la misma oposición. Los vectores colineales pueden escribirse como múltiplos escalares entre sí. Si dos vectores \( \vec{v} \) y \( \vec{w} \) son colineales, entonces existe un escalar \(k\) tal que \( \vec{v} = k \vec{w} \) o \( \vec{w} = k \vec{v} \). Esto significa que un vector es un múltiplo escalar del otro y apuntan en la misma o en direcciones opuestas.

Vectores ortogonales: Dos vectores son ortogonales si su producto punto es cero. Los vectores ortogonales también se llaman vectores perpendiculares, y forman un ángulo de 90 grados entre ellos.

Vectores de base: Un conjunto de vectores de base es un conjunto de vectores linealmente independientes que se pueden usar para representar cualquier otro vector en un espacio. Los vectores de base más comunes son los vectores unitarios estándar en el espacio tridimensional, que se denotan por \(\hat{i}\), \(\hat{j}\) y \(\hat{k}\).

Independencia lineal: Un conjunto de vectores es linealmente independiente si ninguno de los vectores en el conjunto puede expresarse como una combinación lineal de los demás. Si un conjunto de vectores es linealmente independiente, entonces puede usarse como una base para un espacio vectorial.

Generación: La generación de un conjunto de vectores es el conjunto de todas las combinaciones lineales de esos vectores. La generación de un conjunto de vectores es un subespacio del espacio vectorial que contiene esos vectores.

Proyección: La proyección de un vector sobre otro es el componente del primer vector que yace en la dirección del segundo vector. La proyección del vector \( \vec{u} \) sobre el vector \( \vec{v} \) está dada por $$ \text{proj}_{\vec{v}} ( \vec{u} ) = \frac{\vec{u} \cdot \vec{v}}{||\vec{v}||^2} \vec{v} $$

Componente: La componente de un vector a lo largo de otro es la parte del primer vector que yace en la dirección del segundo vector. La componente del vector \( \vec{u} \) a lo largo del vector \( \vec{v} \) está dada por $$ \text{comp}_{\vec{v}} (\vec{u}) = \frac{\vec{u} \cdot \vec{v}}{||\vec{v}||^2} \cos \theta $$ donde \( \theta \) es el ángulo entre \( \vec{u} \) y \( \vec{v} \).

Transporte paralelo: El transporte paralelo es una forma de mover vectores a lo largo de una curva de manera que preserve su dirección. El transporte paralelo se utiliza en geometría diferencial y otros campos para estudiar la curvatura de curvas y superficies.

Covarianza y contravarianza: En matemáticas y física, los vectores a menudo se clasifican como covariantes o contravariantes según cómo se transforman sus componentes bajo transformaciones de coordenadas. Los vectores covariantes tienen componentes que se transforman de la misma manera que las coordenadas, mientras que los vectores contravariantes tienen componentes que se transforman en la dirección opuesta. El concepto de covarianza y contravarianza se utiliza extensamente en cálculo tensorial y otras áreas de matemáticas y física.

Estas son solo algunas de las muchas propiedades de los vectores.

La longitud de un vector (Magnitud) ☰

En matemáticas, la longitud de un vector también se conoce como su magnitud o norma. Representa la distancia entre el origen y el extremo del vector en un espacio geométrico.
Para un vector con componentes \( (x, y, z) \) en un espacio tridimensional, su longitud se puede calcular utilizando la siguiente fórmula:
\( |\vec{v}| = \sqrt{(x^2+ y^2+ z^2 )} \).

En el espacio bidimensional, la fórmula para la longitud de un vector con componentes \((x, y)\) es: $$ |\vec{v}| = \sqrt{(x^2+ y^2 )}. $$ En general, la longitud de un vector se puede calcular utilizando el teorema de Pitágoras, que establece que el cuadrado de la longitud del vector es igual a la suma de los cuadrados de sus componentes.

La dirección de un vector ☰

La dirección de un vector puede determinarse calculando su ángulo con respecto a un eje de referencia. Este ángulo se mide comúnmente en sentido antihorario desde la dirección positiva del eje de referencia.
Si \( \vec{v} \) es un vector en el espacio bidimensional con componentes \( (v_x,v_y ) \), entonces su dirección \( \theta \) está dada por: \( \theta = \arctan \left( \frac{v_y}{v_x} \right) \), donde arctan es la función tangente inversa.

En el espacio tridimensional, un vector \( \vec{v} \) con componentes \( (v_x,v_y,v_z ) \) puede representarse como un segmento de línea dirigido desde el origen \( (0,0,0) \) hasta el punto \( (v_x,v_y,v_z ) \). Su dirección puede describirse mediante dos ángulos: el ángulo azimutal \( \varphi \), que es el ángulo medido en sentido antihorario desde el eje \(x\)-positivo en el plano \(xy\), y el ángulo polar \( \theta \), que es el ángulo medido desde el eje \(z\)-positivo hasta el segmento de línea.

El ángulo azimutal \( \varphi \) está dado por: \( \varphi = \arctan \left( \frac{v_y}{v_x} \right) \).
Si \( v_x > 0 \), entonces \( \varphi = \arctan \left( \frac{v_y}{v_x} \right) \).
Si \( v_x < 0 \), entonces \( \varphi=\arctan \left( \frac{v_y}{v_x} \right) + \pi \).
El ángulo polar \( \theta \) está dado por: \( \theta = \arccos \left( \frac{v_z}{|\vec{v}|} \right) \), donde \( |\vec{v}| \) es la magnitud del vector \( \vec{v} \).

Otra forma de describir la dirección de un vector en el espacio tridimensional es mediante sus cosenos directores. Los cosenos directores de un vector \( \vec{v} \) con componentes \( (v_x,v_y,v_z ) \) se definen como: \( \cos \alpha = \frac{v_x}{|\vec{v}|} \), \( \cos \beta = \frac{v_y}{|\vec{v}|} \), \( \cos \gamma = \frac{v_z}{|\vec{v}|} \), donde \( \alpha \), \( \beta \) y \( \gamma \) son los ángulos entre el vector \( \vec{v} \) y los ejes positivos \(x\), \(y\) y \(z\), respectivamente.

Si los cosenos directores de un vector son conocidos, su dirección puede determinarse utilizando las siguientes ecuaciones: $$ \varphi = \begin{cases} \arccos \left( \frac{\cos \beta}{\sqrt{\cos^2 \alpha + \cos^2 \beta}} \right) & \text{si } \cos \alpha > 0 \\ 2\pi - \arccos \left( \frac{\cos \beta}{\sqrt{\cos^2 \alpha + \cos^2 \beta}} \right) & \text{si } \cos \alpha < 0 \end{cases} $$
\( \theta = \arccos (\cos \gamma) \), donde \( \varphi \) es el ángulo azimutal y \( \theta \) es el ángulo polar.

Además de estos métodos, la dirección de un vector también puede describirse utilizando vectores unitarios. Un vector unitario es un vector con magnitud 1 que apunta en la misma dirección que el vector original. Dado un vector \( \vec{v} \), su vector unitario \( \hat{v} \) se puede calcular como: \( \hat{v} = \frac{\vec{v}}{|\vec{v}|} \).

Una vez que se conoce el vector unitario, su dirección puede describirse mediante los ángulos \( \theta \) y \( \varphi \) como se describió anteriormente.
Cabe destacar que la dirección de un vector es independiente de su magnitud. Por lo tanto, un vector y un múltiplo escalar de ese vector tienen la misma dirección.

Adición y sustracción de vectores colineales ☰

Los vectores colineales son vectores que se encuentran en la misma línea. Cuando se suman o restan dos vectores colineales, el resultado es otro vector colineal. La magnitud del resultado es la suma o diferencia de las magnitudes de los dos vectores, dependiendo de si los estamos sumando o restando. La dirección del resultado es la misma que la de los dos vectores, ya que son colineales.

Supongamos que tenemos dos vectores colineales \( \vec{a} \) y \( \vec{b} \), con magnitudes \( |\vec{a}| \) y \( |\vec{b}| \) respectivamente. Si apuntan en la misma dirección, su suma está dada por: \( \vec{a} + \vec{b} = (|\vec{a}| + |\vec{b}|) \hat{a} \), donde \( \hat{a} \) es el vector unitario en la dirección de \( \vec{a} \). Si apuntan en direcciones opuestas, su diferencia está dada por: \( \vec{a} - \vec{b} = (|\vec{a}| - |\vec{b}|) \hat{a} \)

Métodos de adición y sustracción de vectores no colineales ☰

Los vectores no colineales son vectores que no se encuentran en la misma línea. Cuando sumamos o restamos vectores no colineales, utilizamos la ley del paralelogramo o la ley del triángulo, dependiendo de la situación.

Ley del Paralelogramo
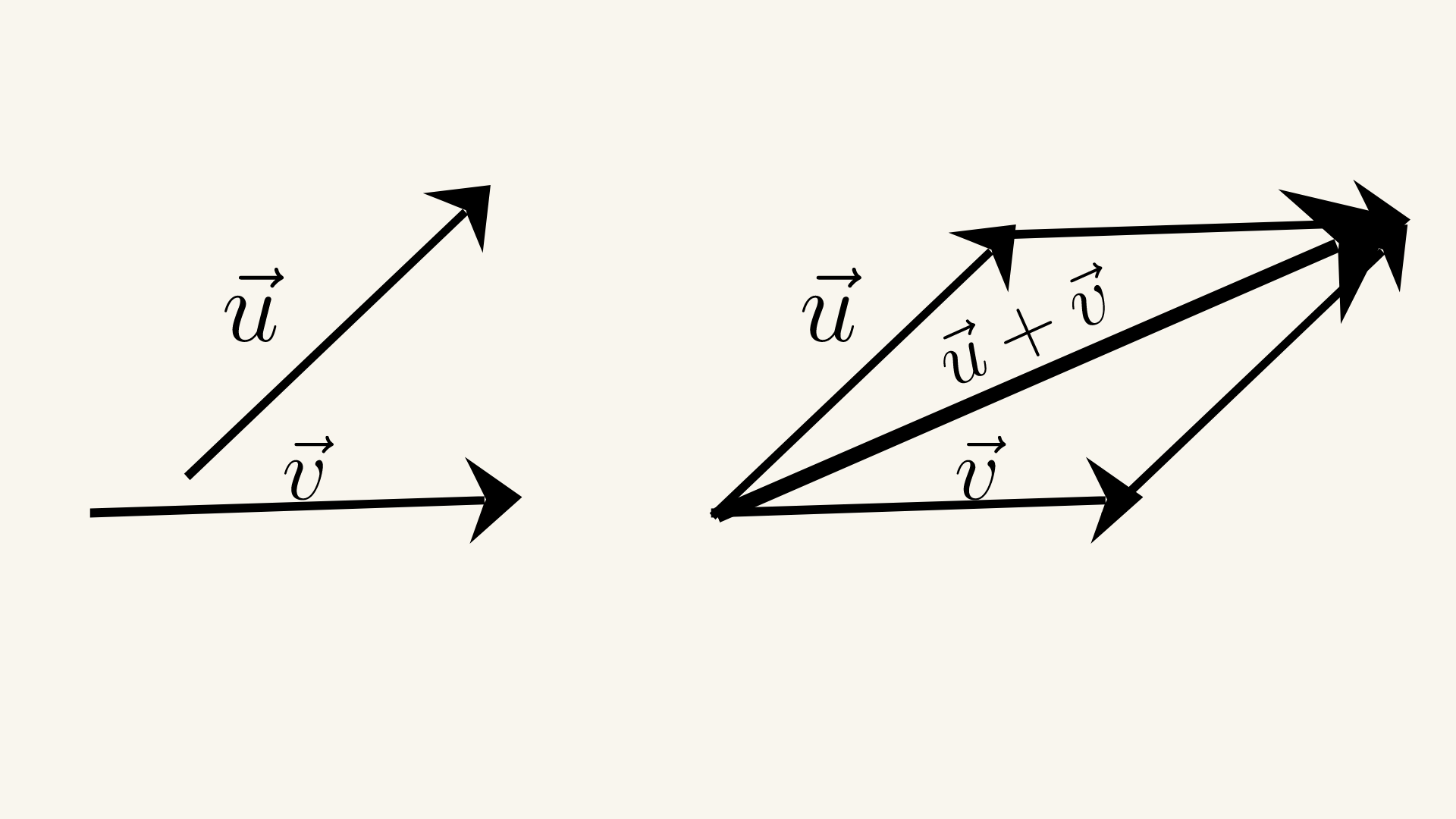
La ley del paralelogramo establece que la suma de dos vectores se puede encontrar colocando los vectores cabeza a cola y dibujando el paralelogramo formado por los dos vectores. La suma vectorial es la diagonal del paralelogramo que comienza desde el punto común de los dos vectores. La ley del paralelogramo se puede usar para sumar cualquier cantidad de vectores, no solo dos. Supongamos que tenemos dos vectores no colineales \( \vec{a} \) y \( \vec{b} \). Podemos encontrar su suma \( \vec{c} \) usando la ley del paralelogramo: \( \vec{c} = \vec{a}+\vec{b} \).
Primero colocamos la cola del vector \( \vec{b} \) en la cabeza del vector \( \vec{a} \) para formar un paralelogramo. La diagonal del paralelogramo que comienza desde el punto común de los dos vectores representa el vector suma \( \vec{c} \). La magnitud del vector suma \( \vec{c} \) se puede encontrar usando la ley de los cosenos: \( |\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + 2|\vec{a}||\vec{b}| \cos \theta \), donde \( \theta \) es el ángulo entre los vectores \( \vec{a} \) y \( \vec{b} \).


Ley del Triángulo
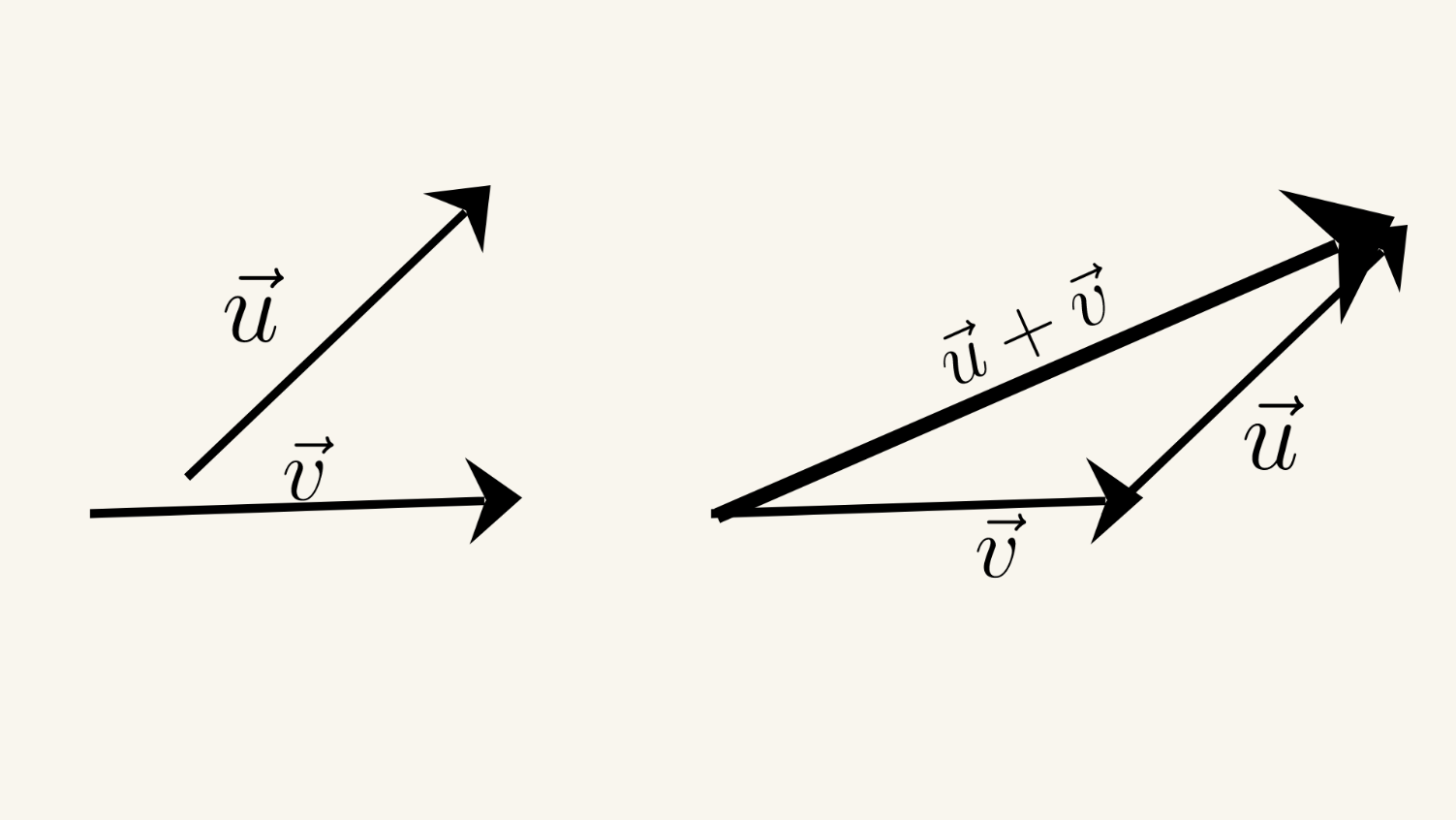
La ley del triángulo establece que la suma de dos vectores se puede encontrar colocando los vectores cabeza a cola y dibujando el tercer lado del triángulo que conecta la cola del primer vector con la cabeza del segundo vector. El vector suma es la diagonal del triángulo que comienza desde el punto común de los dos vectores. Supongamos que tenemos dos vectores no colineales \( \vec{a} \) y \( \vec{b} \). Podemos encontrar su suma \( \vec{c} \) usando la ley del triángulo: \( \vec{c}= \vec{a}+ \vec{b} \).
Primero colocamos la cola del vector \( \vec{a} \) en el origen y luego colocamos la cola del vector \( \vec{b} \) en la cabeza del vector \( \vec{a} \). El vector suma \( \vec{c} \) es la diagonal del triángulo que comienza desde el origen y conecta la cabeza del vector \( \vec{b} \). La magnitud del vector suma \( \vec{c} \) se puede encontrar usando la ley de los cosenos: \( |\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 -2|\vec{a}||\vec{b}| \cos \theta \), donde \( \theta \) es el ángulo entre los vectores \( \vec{a} \) y \( \vec{b} \).
La resta de vectores también se puede hacer utilizando la ley del paralelogramo o la ley del triángulo. Para restar el vector \( \vec{b} \) del vector \( \vec{a} \), simplemente invertimos la dirección del vector \( \vec{b} \) y lo sumamos al vector \( \vec{a} \) utilizando la ley del paralelogramo o la ley del triángulo. \( \vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \).


Propiedades de la adición de vectores
La adición de vectores tiene varias propiedades importantes que la hacen útil en física y otros campos:

• Propiedad conmutativa: El orden en que se suman los vectores no afecta el resultado.
  \( \vec{a} + \vec{b} = \vec{b} + \vec{a} \).
• Propiedad asociativa: Al sumar más de dos vectores, el orden en que agrupamos los vectores no afecta el resultado.
  \( (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \).
• Vector nulo: El vector nulo \( \vec{0} \), con magnitud cero y cualquier dirección, es la identidad aditiva para vectores. Sumar el vector nulo a cualquier vector no cambia el vector.
  \( \vec{a} + \vec{0} = \vec{a} \).
• Inverso aditivo: Para cada vector \( \vec{a} \), existe un vector inverso aditivo \( -\vec{a} \) tal que su suma es el vector nulo.
  \( \vec{a} + (-\vec{a}) = \vec{0} \).
• Propiedad distributiva: La multiplicación escalar se distribuye sobre la adición de vectores.
  \( (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b} \), donde \(k\) es cualquier escalar.

Suma de vectores usando componentes ☰

Cuando sumamos vectores usando componentes, el primer paso es descomponer cada vector en sus componentes \(x\) y \(y\). Esto se puede hacer usando funciones trigonométricas como el seno y el coseno. Por ejemplo, dado un vector con magnitud "\(r\)" y ángulo "\(\theta \)" con respecto al eje \(x\), sus componentes \(x\) y \(y\) se pueden encontrar de la siguiente manera:
Componente \(x\): \(r\cdot cos(\theta) \).
Componente \(y\): \(r\cdot sin(\theta) \).

Una vez que ambos vectores se han descompuesto en sus componentes \(x\) y \(y\), las componentes se pueden sumar por separado. Por ejemplo, si tenemos dos vectores \(A\) y \(B\), sus componentes \(x\) se pueden sumar para obtener la componente \(x\) del vector resultante \(C\), y sus componentes \(y\) se pueden sumar para obtener la componente \(y\) de \(C\):
\(C_x = A_x+ B_x \)
\(C_y= A_y+ B_y \)

Finalmente, la magnitud y el ángulo del vector \(C\) se pueden encontrar usando el teorema de Pitágoras y funciones trigonométricas inversas, respectivamente:
Magnitud de \(C\): \( \sqrt{C_x^2 + C_y^2} \) .
Ángulo de \(C\): \( tan^{-1} \left(\frac{C_y}{C_x} \right) \) .
Tenga en cuenta que el ángulo de \(C\) puede necesitar ajustarse según en qué cuadrante se encuentre, ya que las funciones trigonométricas inversas solo dan ángulos en el rango de \( -\frac{\pi}{2} \) a \( \frac{\pi}{2} \).

Para ajustar el ángulo del vector \( \vec{C} \), debemos considerar los signos de sus componentes \(x\) y \(y\). Si \(C_x\) y \(C_y\) son ambos positivos, entonces el ángulo de \(C\) es simplemente la tangente inversa de \( \frac{C_y}{C_x} \). Si \(C_x\) es negativo y \(C_y\) es positivo, entonces el ángulo de \(C\) es 180 grados menos la tangente inversa de \( \frac{C_y}{|C_x|} \). Si \(C_x\) es negativo y \(C_y\) es negativo, entonces el ángulo de \(C\) es 180 grados más la tangente inversa de \( \frac{|C_y |}{|C_x |} \). Finalmente, si \(C_x\) es positivo y \(C_y\) es negativo, entonces el ángulo de \(C\) es 360 grados menos la tangente inversa de \( \frac{|C_y|}{C_x} \).

Por ejemplo, supongamos que tenemos dos vectores \(A\) y \(B\) con magnitudes de 3 y 4, respectivamente, y ángulos de 30 grados y 60 grados con respecto al eje \(x\). Podemos encontrar las componentes \(x\) y \(y\) de cada vector de la siguiente manera:
\( A_x = 3 \cdot cos(30) = 2.598 \)
\( A_y = 3 \cdot sin(30)= 1.5 \)
\( B_x = 4 \cdot cos(60)= 2 \)
\( B_y = 4 \cdot sin(60)= 3.464 \)

Luego podemos sumar las componentes \(x\) y \(y\) de \(A\) y \(B\) para obtener las componentes \(x\) y \(y\) de \(C\):
\( C_x = A_x + B_x= 4.598 \)
\( C_y = A_y + B_y= 4.964 \)

La magnitud de \( \vec{C} \) es:
\( \small \vec{|C|} = \sqrt{C_x^2+ C_y^2} = \sqrt{4.598^2 + 4.964^2} = 6.425 \)

El ángulo de \(C\) es:
\( \small \theta = tan^{-1} \left(\frac{C_y}{C_x} \right) = tan^{-1} \left(\frac{4.964}{4.598} \right) = 49.1^\circ \)

Dado que tanto \(C_x\) como \(C_y\) son positivos, esta es la respuesta final. Por lo tanto, el vector resultante \(C\) tiene una magnitud de 6.425 y un ángulo de 49.1 grados con respecto al eje \(x\).

Multiplicación escalar ☰

La multiplicación escalar es la operación de multiplicar un vector por un escalar, que es un número real. Cuando un vector se multiplica por un escalar, la magnitud del vector se escala por el valor absoluto del escalar, y la dirección del vector no cambia si el escalar es positivo, o se invierte si el escalar es negativo.
Matemáticamente, la multiplicación escalar se puede expresar de la siguiente manera: dado un vector \(v\) y un escalar \(k\), el múltiplo escalar de \( \vec{v} \) por \(k\), denotado \( k \cdot \vec{v} \), es un vector con la misma dirección que \( \vec{v} \) pero con una magnitud escalada por el valor absoluto de \(k\):
\( k \cdot \vec{v} = (|k|) \cdot \vec{v} \)

Si \(k\) es positivo, entonces la dirección de \( k \cdot \vec{v} \) es la misma que la dirección de \( \vec{v} \). Si \(k\) es negativo, entonces la dirección de \( k \cdot \vec{v} \) es opuesta a la dirección de \( \vec{v} \).

La multiplicación escalar se puede utilizar para estirar o encoger vectores. Por ejemplo, si tenemos un vector \( \vec{v} \) que representa un desplazamiento en metros, podemos multiplicarlo por un escalar para representar un desplazamiento que sea más grande o más pequeño que \( \vec{v} \). Además, la multiplicación escalar se puede utilizar para invertir la dirección de un vector multiplicándolo por \(-1\).

La multiplicación escalar también se puede utilizar para encontrar combinaciones lineales de vectores. Una combinación lineal de dos vectores es simplemente la suma de los vectores multiplicados por coeficientes escalares.
Por ejemplo, dados dos vectores \( \vec{v} = (2,3) \) y \( \vec{w} = (1,-1) \), la combinación lineal \( 3 \vec{v} – 2 \vec{w} \) se puede calcular de la siguiente manera: $$ \begin{align*} &3\vec{v} = 3(2,3) = (6,9)& \\ &2\vec{w} = 2(1,-1) = (2,-2)& \\ &3\vec{v} - 2\vec{w} = (6,9) - (2,-2) = (4,11)& \end{align*} $$ El vector resultante \((4,11)\) es una combinación lineal de \( \vec{v} \) y \( \vec{w} \) con coeficientes \(3\) y \(-2\), respectivamente.

La multiplicación escalar también satisface varias propiedades importantes:

• Distributividad: Para cualquier escalar \(k\) y \(l\) y cualquier vector \( \vec{v} \), tenemos \( (k+l) \vec{v} = k \vec{v} + l \vec{v} \).
• Asociatividad: Para cualquier escalar \(k\) y cualquier vectores \( \vec{u} \) y \( \vec{v} \), tenemos \( k( \vec{u} + \vec{v} ) = k \vec{u} + k \vec{v} \).
• Compatibilidad con la multiplicación: Para cualquier escalares \(k\) y \(l\) y cualquier vector \( \vec{v} \), tenemos \( (kl) \vec{v} = k(l \vec{v}) \).

Estas propiedades hacen que la multiplicación escalar sea una herramienta útil para manipular y resolver sistemas de ecuaciones lineales.

Transporte paralelo ☰

El transporte paralelo es un concepto en geometría diferencial que describe cómo un vector o un espacio tangente a lo largo de una curva puede ser transportado a lo largo de la curva sin cambiar su dirección. Es un concepto importante para entender la geometría de espacios curvos.

En general, una curva en una variedad es un camino que conecta dos puntos en la variedad. Un vector tangente es un vector que es tangente a la curva en un punto particular. El transporte paralelo a lo largo de una curva es el proceso de mover un vector tangente a lo largo de la curva mientras se mantiene tangente a la curva en cada punto.

La idea del transporte paralelo está estrechamente relacionada con el concepto de conexión en una variedad. Una conexión es una forma de conectar espacios tangentes en diferentes puntos de una variedad. Permite la comparación de vectores tangentes en diferentes puntos de una curva.

Para definir el transporte paralelo, es necesario especificar una conexión en la variedad. Dada una conexión, el transporte paralelo de un vector a lo largo de una curva se define como el vector único que es tangente a la curva en cada punto y cuyos componentes en una base particular permanecen constantes a lo largo de la curva.

El concepto de transporte paralelo es importante en muchas áreas de la física, incluida la relatividad general, donde se utiliza para describir el transporte de tensores a lo largo de trayectorias de espacio-tiempo curvadas.

Transformación y figuras congruentes ☰

La transformación se refiere al proceso de cambiar la posición, el tamaño o la forma de una figura geométrica. Hay varios tipos de transformaciones, incluyendo traslaciones, reflexiones, rotaciones y dilataciones. Las figuras congruentes son figuras geométricas que tienen el mismo tamaño y forma, y sus lados y ángulos correspondientes son congruentes.

Aquí hay algunos teoremas importantes relacionados con las transformaciones y las figuras congruentes:

• Partes correspondientes de figuras congruentes son congruentes (CPCTC): Este teorema establece que si dos figuras son congruentes, entonces sus lados, ángulos y vértices correspondientes son congruentes.
• La composición de traslaciones es una traslación: Si se realizan dos traslaciones una después de la otra, entonces la transformación resultante también es una traslación.
• La composición de reflexiones es una rotación o una traslación: Si se realizan dos reflexiones una después de la otra, entonces la transformación resultante es una rotación o una traslación.
• La composición de rotaciones es una rotación: Si se realizan dos rotaciones una después de la otra, entonces la transformación resultante también es una rotación.
• La composición de una dilatación y una traslación es una dilatación: Si se realiza una dilatación y una traslación una después de la otra, entonces la transformación resultante también es una dilatación.
• La composición de una dilatación y una rotación es una dilatación o una rotación: Si se realiza una dilatación y una rotación una después de la otra, entonces la transformación resultante es una dilatación o una rotación.
• La composición de dos transformaciones congruentes es una transformación congruente: Si dos transformaciones son congruentes, entonces su composición también es congruente.

Estos teoremas son importantes para entender las propiedades de las transformaciones y las figuras congruentes, y se pueden utilizar para demostrar varios teoremas geométricos y resolver problemas en geometría.