Sólidos Curvos: Guía de Esferas, Conos y Cilindros

    Introducción a los Sólidos Curvos

    Clasificación de Sólidos Curvos

    Sólidos Convexos
    Sólidos donde cualquier segmento de línea que conecta dos puntos dentro del sólido yace completamente dentro del sólido. Los ejemplos incluyen esferas, conos y cilindros.
    Sólidos No Convexos
    Sólidos donde algunos segmentos de línea que conectan puntos internos pueden yacer parcialmente fuera del sólido. Los ejemplos incluyen toros y poliedros cóncavos.

    Teoremas Fundamentales

    Teorema del Centroide de Pappus
    Establece que el volumen de un sólido de revolución es igual al producto del área de la figura generadora y la longitud de la trayectoria rotacional de su centroide.
    Principio de Cavalieri
    Si dos sólidos tienen alturas iguales y áreas de sección transversal iguales en cada altura, sus volúmenes son iguales.

    Propiedades de la Geometría Esférica

    • Líneas Paralelas: No existen en geometría esférica
    • Ángulos del Triángulo: La suma excede 180 grados
    • Cálculo del Área: Proporcional al exceso angular

    Esfera

    Un sólido perfectamente simétrico donde todos los puntos de la superficie están equidistantes del centro.

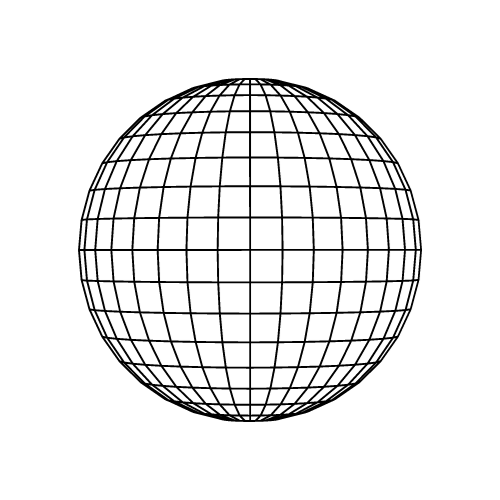
    Esfera
    Esfera

    Fórmulas Clave

    Área de Superficie
    \(SA = 4\pi r^2\)
    Volumen
    \(V = \frac{4}{3}\pi r^3\)
    Diámetro
    \(D = 2r\)

    Propiedades

    • Distancia igual desde el centro a todos los puntos de la superficie
    • Área de superficie mínima para un volumen dado
    • Infinitas líneas de simetría
    • Relación óptima volumen-área de superficie

    Aplicaciones en el Mundo Real

    • Cuerpos Celestes: Las fuerzas gravitacionales crean planetas aproximadamente esféricos
    • Gotas de Líquido: La tensión superficial forma formas esféricas
    • Recipientes a Presión: Tanques esféricos para una distribución óptima de la presión

    Cono

    Un sólido formado al conectar todos los puntos de una base plana a un único punto vértice.

    Cono
    Cono

    Fórmulas Esenciales

    Área de Superficie Lateral
    \(S_{LSA} = \pi rl\)
    Área de Superficie Total
    \(S_{SA} = \pi r(r+l)\)
    Volumen
    \(V = \frac{1}{3}\pi r^2h\)
    Altura Inclinada
    \(l = \sqrt{r^2 + h^2}\)

    Tronco de Cono

    Una sección del cono formada por cortes paralelos a la base.

    \(V = \frac{1}{3}\pi h(R^2 + r^2 + Rr)\)

    Cilindro

    Un sólido con bases paralelas congruentes conectadas por una superficie curva.

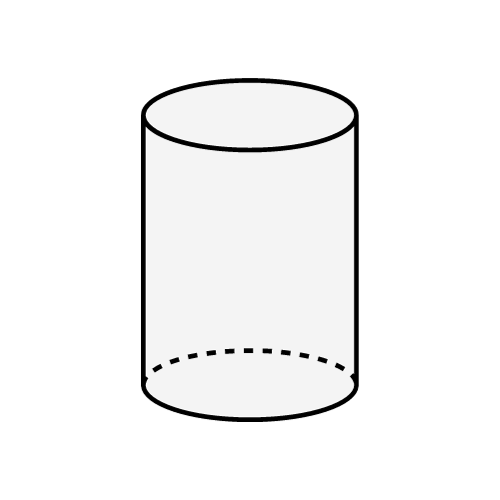
    Cilindro
    Cilindro

    Fórmulas Principales

    Área de Superficie
    \(SA = 2\pi r^2 + 2\pi rh\)
    Área de Superficie Lateral
    \(LSA = 2\pi rh\)
    Volumen
    \(V = \pi r^2h\)

    Tipos de Cilindros

    Cilindro Circular Recto
    Base circular con eje perpendicular
    Cilindro Elíptico
    Base elíptica con fórmula de volumen: \(V = \pi abh\)

    Aplicaciones

    • Ingeniería: Tuberías, columnas, tanques de almacenamiento
    • Óptica: Lentes cilíndricas para corrección de astigmatismo
    • Arquitectura: Soportes estructurales y elementos decorativos