Función cuadrática y su gráfica ☰

Una función cuadrática es una función polinómica de grado dos. Se define por la fórmula: \( f(x)=ax^2+bx+c \), donde \(a\), \(b\) y \(c\) son constantes, y \(a\) no es igual a cero.
La gráfica de una función cuadrática es una parábola, que es una curva en forma de U. La dirección de la parábola depende del signo del coeficiente principal \(a\). Si \(a\) es positivo, la parábola se abre hacia arriba, y si \(a\) es negativo, la parábola se abre hacia abajo.
El vértice de la parábola se calcula mediante la fórmula: \(\left(-\frac{b}{2a}, \frac{4ac - b^2}{4a}\right)\).

El eje de simetría de la parábola es la línea vertical que pasa por el vértice, dada por la ecuación \(x=-\frac{b}{2a}\)

Las intersecciones (\(x\)-interceptos) de la función cuadrática se calculan mediante la fórmula cuadrática: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
Si el discriminante \(b^2-4ac\) es positivo, la función cuadrática tiene dos raíces reales distintas, que son las coordenadas \(x\) de los \(x\)-interceptos. Si el discriminante es cero, la función cuadrática tiene una raíz real, que es la coordenada \(x\) del vértice. Si el discriminante es negativo, la función cuadrática no tiene raíces reales, sino dos raíces complejas conjugadas.

Las funciones cuadráticas también pueden expresarse en forma factorizada: \( f(x)=a(x-r_1 )(x-r_2 ) \), donde \(r_1\) y \(r_2\) son las raíces de la función cuadrática. Esta forma es útil para encontrar las raíces de la función.
La forma del vértice de la función cuadrática es: \( f(x)=a(x-h)^2 +k \), donde \( (h,k) \) es el vértice de la parábola. La forma estándar y la forma del vértice de la función cuadrática están relacionadas por: \( f(x)=a(x-h)^2 +k=ax^2 -2ahx+ah^2 +k \), lo que muestra que \(a\), \(b=-2ah\), y \( c=ah^2 +k\) están relacionados con el vértice \( (h,k) \).
La función cuadrática se puede graficar trazando el vértice, el eje de simetría y los \(x\)-interceptos. Para esbozar la gráfica, también podemos encontrar el valor máximo o mínimo de la función, el dominio, el rango y cualquier transformación o desplazamiento.

Valor máximo o mínimo de la función cuadrática:
Si \( a > 0 \), la parábola se abre hacia arriba y el vértice es el punto mínimo de la función. El valor mínimo es \( f(h)=k \). Si \( a < 0 \), la parábola se abre hacia abajo y el vértice es el punto máximo de la función. El valor máximo es \(f(h)=k\).

Dominio y rango de la función cuadrática:
El dominio de la función cuadrática es el conjunto de todos los números reales, ya que la función está definida para todos los valores de \(x\). El rango depende del signo del coeficiente principal \(a\). Si \(a>0\), el rango es \( \left [k, \infty \right ) \) y si \(a < 0 \), el rango es \( \left ( - \infty ,k \right ] \).

Gráfica:
La gráfica de una función cuadrática puede transformarse cambiando los valores de \(a\), \(b\) y \(c\). Por ejemplo, si \(a\) se multiplica por una constante positiva, la gráfica se estira verticalmente, y si \(a\) se multiplica por una constante negativa, la gráfica se refleja sobre el eje \(x\). Si se suma o resta \(b\) a \(x\), la gráfica se desplaza horizontalmente y si se suma o resta \(c\) a \(f(x)\), la gráfica se desplaza verticalmente.

Función de Valor Absoluto (y=|x|) y su gráfica ☰

La función \( f(x)=|x| \) es una función definida por partes que toma el valor absoluto de la entrada \(x\). La función de valor absoluto se define de la siguiente manera:

\( | x | = \begin{cases} -x & \text{, } x < 0 \\ x & \text{, } x \geq 0 \end{cases} \)

Por lo tanto, la función \(f(x)=|x|\) toma el valor \(x\) cuando \(x\) es no negativo, y \(-x\) cuando \(x\) es negativo. La gráfica de \( f(x)=|x| \) es una curva en forma de V con el vértice en el origen. La pendiente de la curva cambia en \(x=0\), donde la función no es diferenciable.

Aquí hay algunas propiedades importantes de la función de valor absoluto:
Simetría: La función \(f(x)=|x|\) es simétrica respecto al origen, lo que significa que \(f(x)=f(-x) \) para todos \(x\).

Valores no negativos: El valor absoluto de cualquier número real es no negativo, lo que significa que \( |x| \ge 0 \) para todos \(x\).

Distancia: El valor absoluto de un número representa su distancia desde cero en la recta numérica. Por ejemplo, \(|3|=3\) y \(|-5|=5\).

Función definida por partes: La función de valor absoluto es una función definida por partes, lo que significa que se define de manera diferente para diferentes intervalos de la entrada \(x\). En particular, \(f(x)=x\) cuando \(x \ge 0 \) y \( f(x)=-x \) cuando \(x < 0 \).

Aplicaciones: La función de valor absoluto se utiliza en una variedad de aplicaciones, como medir la diferencia entre dos valores, calcular distancias y resolver ecuaciones de valor absoluto.

Gráfica:

Para resumir, la función de valor absoluto es una función definida por partes que toma el valor no negativo de su entrada si es no negativa, y el negativo de su entrada si es negativa. La gráfica de \(f(x)=|x| \) es una curva en forma de V que es simétrica respecto al origen.

Función cúbica y su gráfica ☰

La función \(f(x)=x^3\) es una función cúbica que toma la entrada \(x\) y la eleva al cubo. La gráfica de \(f(x)=x^3 \) es una curva que pasa por el origen y tiene una forma similar a la letra "S". La función está definida para todos los valores reales de \(x\).

Aquí hay algunas propiedades importantes de la función cúbica:
Dominio y rango: El dominio de la función \(f(x)=x^3 \) son todos los números reales, lo que significa que cualquier número real puede ser ingresado en la función. El rango de la función también son todos los números reales, lo que significa que la salida puede tomar cualquier valor real.

Simetría: La función \(f(x)=x^3 \) es una función impar, lo que significa que \(f(-x)=-f(x) \) para todos \(x\). Esta propiedad hace que la gráfica de la función sea simétrica respecto al origen.

Interceptos: La función \(f(x)=x^3 \) pasa por el origen, lo que significa que tiene un intercepto en \(y\) de cero. La función no tiene ningún intercepto en \(x\).

Intervalos crecientes y decrecientes: La función \(f(x)=x^3 \) es creciente para todos los \(x\), lo que significa que el valor de la función aumenta a medida que \(x\) aumenta. Esta propiedad hace que la gráfica de la función sea ascendente. La función no tiene ningún máximo o mínimo local.

Aplicaciones: La función cúbica se utiliza en una variedad de aplicaciones, como modelar el volumen de un cubo o el crecimiento de una población.

Gráfica


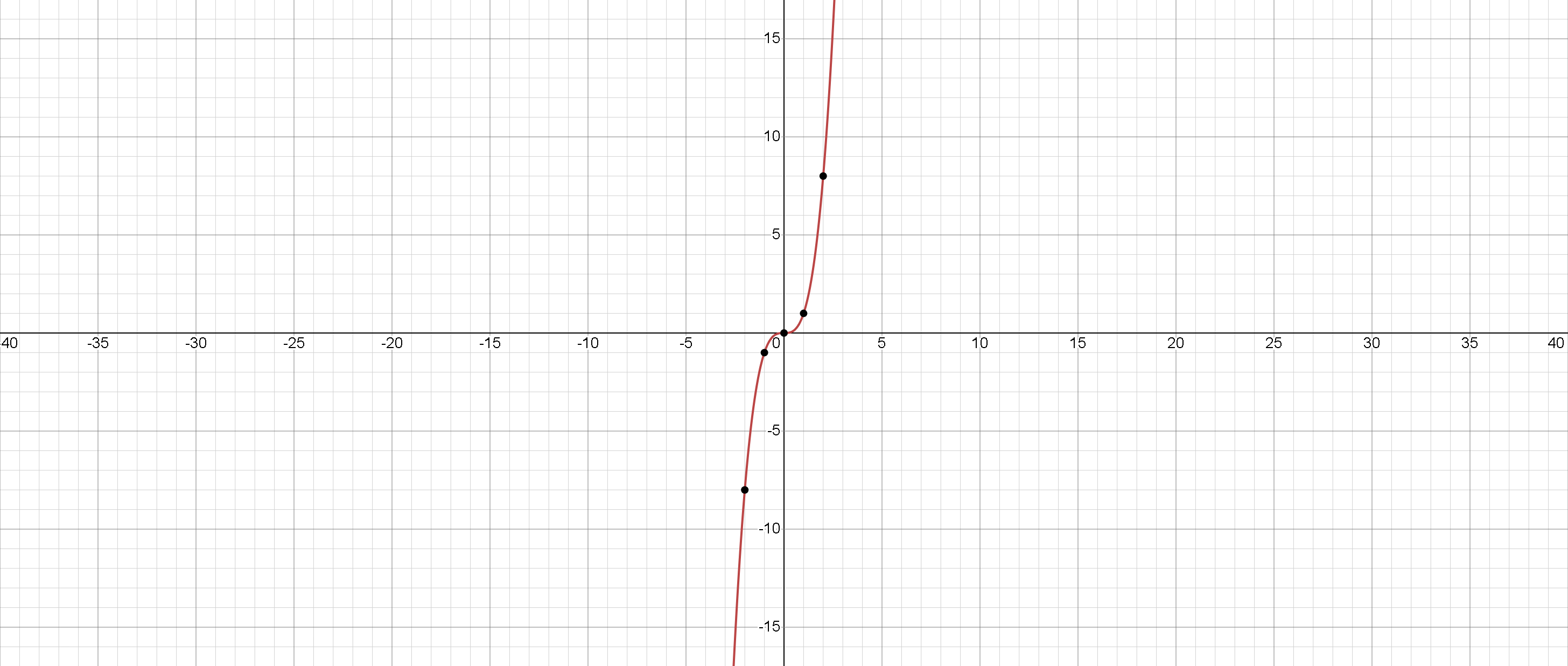
En resumen, la función cúbica \(f(x)=x^3 \) es una función que eleva la entrada \(x\) al cubo. La gráfica de la función es una curva ascendente que pasa por el origen y es simétrica respecto al origen. La función está definida para todos los valores reales de \(x\) y tiene un rango de todos los números reales.