Dominio y Rango de una función ☰

Una función es un objeto matemático que asigna una única salida a cada entrada. El conjunto de todos los posibles valores de entrada se llama dominio de la función, y el conjunto de todas las posibles salidas se llama rango de la función. En otras palabras, el dominio es el conjunto de valores que se pueden introducir en la función, y el rango es el conjunto de valores que la función puede producir.
Formalmente, una función \(f\) es una asignación de un conjunto \(A\) (el dominio) a un conjunto \(B\) (el rango), donde para cada \(a \in A\), hay un único \(b \in B\) tal que \(f(a)=b\). Escribimos \(f\): \(A \rightarrow B\) para denotar que \(f\) es una función de \(A\) a \(B\).
Por ejemplo, considera la función \(f(x)=x^2\), donde \(x\) es un número real. El dominio de \(f\) es el conjunto de todos los números reales, porque cualquier número real se puede introducir en \(f\). Sin embargo, el rango de \(f\) es solo el conjunto de números reales no negativos, porque \(f(x)\) siempre es no negativo.
Al encontrar el dominio y el rango de una función, hay algunas cosas que tener en cuenta:

• El dominio de una función es el conjunto de todas las posibles entradas. Esto significa que cualquier valor que haga que la función no esté definida (como dividir por cero o tomar la raíz cuadrada de un número negativo) no puede estar en el dominio.
• El rango de una función es el conjunto de todas las posibles salidas. Esto significa que la función solo puede producir valores que estén en el rango.
• Es posible que diferentes funciones tengan el mismo dominio o rango. Por ejemplo, las funciones \(f(x)=x^2\) y \(g(x)=|x|\) tienen el mismo dominio de todos los números reales, pero sus rangos son diferentes.
• El dominio y el rango de una función pueden determinarse analizando la gráfica de la función. El dominio es el conjunto de todos los valores de \(x\) posibles que aparecen en la gráfica, y el rango es el conjunto de todos los valores de \(y\) posibles que aparecen en la gráfica.

Veamos algunos ejemplos para entender mejor cómo encontrar el dominio y el rango de una función.

Ejemplo 1: Encuentra el dominio y el rango de la función \( f(x) = \frac{1}{x} \)
La función \(f(x)\) está definida para todos los \(x \neq 0\) porque la división por cero no está definida. Por lo tanto, el dominio de \(f\) es el conjunto de todos los números reales excepto cero, o \( (-\infty ; 0) \cup (0 ; \infty ) \).
Para encontrar el rango de \(f\), notamos que \(f(x)\) puede ser cualquier número real excepto cero. Esto significa que el rango de \(f\) también es \( (-\infty ; 0 ) \cup ( 0 ; \infty ) \).

Ejemplo 2: Encuentra el dominio y el rango de la función \( f(x) = \sqrt{4-x^2} \).
La función \(f(x)\) está definida solo para valores de \(x\) tales que \( 4 - x^2 \ge 0 \). Resolviendo esta desigualdad, obtenemos \( -2 \le x \le 2 \).
Por lo tanto, el dominio de \(f\) es el intervalo cerrado \([-2,2]\). Para encontrar el rango de \(f\), notamos que \(f(x)\) puede ser cualquier número real no negativo menor o igual a 2. Esto significa que el rango de \(f\) es el intervalo cerrado \([0,2]\).

Ejemplo 3: Encuentra el dominio y el rango de la función \(f(x)=\sin(x) \).
La función \(f(x)\) está definida para todos los números reales, por lo que el dominio de \(f\) es \( (-\infty , \infty) \).
Para encontrar el rango de \(f\), notamos que \(\sin(x)\) puede tomar cualquier valor entre -1 y 1, inclusive. Por lo tanto, el rango de \(f\) es el intervalo cerrado \([-1,1] \).

En resumen, el dominio de una función es el conjunto de todas las posibles entradas, y el rango es el conjunto de todas las posibles salidas. El dominio y el rango se pueden determinar analizando la función misma o su gráfica.

Propiedades de las funciones ☰

Las funciones tienen diversas propiedades que se pueden usar para analizar y compararlas. En esta explicación, discutiremos algunas de las propiedades más importantes de las funciones.

Funciones pares e impares:
Una función \(f\) se dice que es par si \(f(-x)=f(x) \) para todos los \(x\) en el dominio de \(f\). En otras palabras, la función es simétrica respecto al eje \(y\). Un ejemplo de una función par es \(f(x)=x^2 \).
Una función \(f\) se dice que es impar si \(f(-x)=-f(x) \) para todos los \(x\) en el dominio de \(f\). En otras palabras, la función es simétrica respecto al origen. Un ejemplo de una función impar es \(f(x)=x^3 \).

Funciones crecientes y decrecientes:
Una función \(f\) se dice que es creciente en un intervalo si \( f(x_1 ) < f(x_2 ) \) siempre que \(x_1 < x_2\) y \(x_1, x_2 \) están en el dominio de \(f\). En otras palabras, la función está subiendo a medida que \(x\) aumenta. Un ejemplo de una función creciente es \(f(x)=x \).
Una función \(f\) se dice que es decreciente en un intervalo si \( f(x_1 ) > f(x_2 ) \) siempre que \(x_1 < x_2\) y \(x_1, x_2 \) están en el dominio de \(f\). En otras palabras, la función está bajando a medida que \(x\) aumenta. Un ejemplo de una función decreciente es \(f(x)=-x \).

Funciones periódicas:
Una función \(f\) se dice que es periódica si existe un número positivo \(p\) tal que \(f(x+p)=f(x)\) para todos los \(x\) en el dominio de \(f\). En otras palabras, la función se repite después de un intervalo fijo. Un ejemplo de una función periódica es \(f(x)=\sin(x)\).

Funciones inyectivas y sobreyectivas:
Una función \(f\) se dice que es inyectiva (o biyectiva) si para cada \(y\) en el rango de \(f\), hay exactamente un \(x\) en el dominio de \(f\) tal que \(f(x)=y\). En otras palabras, no hay dos entradas distintas que den la misma salida. Un ejemplo de una función inyectiva es \( f(x)=x+1 \).
Una función \(f\) se dice que es sobreyectiva (o suprayectiva) si para cada \(y\) en el rango de \(f\), hay al menos un \(x\) en el dominio de \(f\) tal que \(f(x)=y\). En otras palabras, cada salida en el rango es alcanzada por alguna entrada. Un ejemplo de una función sobreyectiva es \( f(x)=x^2 \).

Funciones biyectivas:
Una función \(f\) se dice que es biyectiva si es tanto inyectiva como sobreyectiva. En otras palabras, cada salida en el rango es alcanzada por exactamente una entrada. Un ejemplo de una función biyectiva es \( f(x)= \sqrt{x} \).

En resumen, las propiedades de las funciones se pueden usar para describir diversos aspectos de la función, como su simetría, dirección, repetición y correspondencia entre las entradas y salidas. Comprender estas propiedades puede ayudar en el análisis y la comparación de funciones en diferentes contextos.

Clasificación de las funciones ☰

Las funciones pueden clasificarse según sus propiedades y comportamiento. En esta explicación, discutiremos las clasificaciones más comunes de las funciones.

Función constante:
\(F(x) = c.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = \{c\}.\)


Función lineal:
\(F(x) = x.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Ceros: \( x=0 \).
Función creciente.
Sin extremos.


Función valor absoluto:
\(F(x) = |x|.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = [0, +\infty).\)
Ceros: \(x = 0.\)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Punto mínimo: \((0, 0).\)


Función racional:
\(F(x) = \frac{1}{x}.\)
\(D(f) = (-\infty, 0) \cup (0, +\infty).\)
\(E(f) = (-\infty, 0) \cup (0, +\infty).\)
\((- \infty, 0) \downarrow \text{, } (0, +\infty) \downarrow.\)
Sin ceros.
Sin extremos.


Función cuadrática:
\(F(x) = x^2.\)
\( D(f) = (-\infty, +\infty). \)
\(E(f) = [0, +\infty). \)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Ceros: \(x = 0.\)
Punto mínimo: \((0, 0).\)


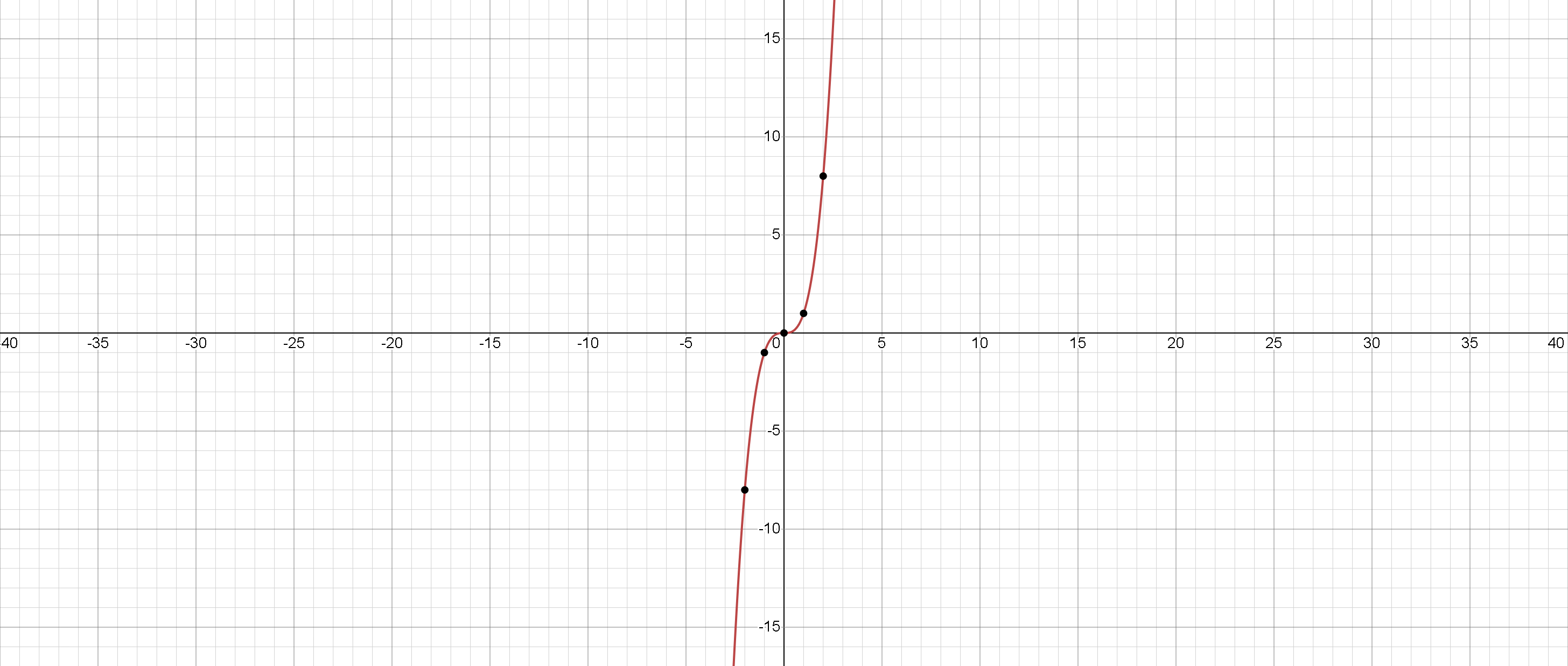
Función cúbica:
\(F(x) = x^3.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Ceros: \(x = 0.\)
Función creciente.
Sin extremos.


Función raíz cuadrada:
\(F(x) = \sqrt{x}.\)
\(D(f) = [0; +\infty).\)
\(E(f) = [0; +\infty).\)
Ceros: \(x = 0.\)
\( [0; +\infty) \uparrow \).
Sin extremos.


Funciones trigonométricas:
Una función trigonométrica es una función que involucra las razones de los lados de un triángulo rectángulo. Ejemplos de funciones trigonométricas incluyen \( \sin(x) \), \( \cos(x) \) y \( \tan(x) \). Las gráficas de las funciones trigonométricas son periódicas y se repiten después de un intervalo fijo.

Funciones por partes:
Una función por partes es una función que está definida por diferentes ecuaciones en diferentes partes de su dominio.

Ejemplos de funciones por partes incluyen:
\( f(x) = \begin{cases} 2x + 1 & \text{si } x < 0 \\ 3x & \text{si } x \geq 0 \end{cases} \)

\( f(x) = \begin{cases} x^2 & \text{si } x \leq -1 \\ -x & \text{si } -1 < x < 1 \\ x & \text{si } x \geq 1 \end{cases} \)

Funciones Potencia o Monomiales ☰

Estas funciones también se conocen como funciones potencia o monomiales.
El valor del exponente \(n\) determina la forma y el comportamiento de la función. Cuando \(n\) es un entero positivo, la función representa un polinomio con un solo término, conocido como monomio. El grado del polinomio es igual al valor de \(n\).

\( F(x)= x^{2k} \):
\( D(f) = (-\infty ; +\infty) \).
\( E(f) = [0; +\infty). \)
Ceros: \(x=0 \).
\( (-\infty; 0] \downarrow \text{, } [0; +\infty) \uparrow \).
\( x_{\text{min}} = 0, f_{\text{min}} = 0 \).
Sin extremos.

\( F(x) = x^{2k+1} \):
\( D(f) = (-\infty ; +\infty). \)
\( E(f) = (-\infty ; +\infty). \)
Ceros: \( x=0 \).
\( (-\infty ; +\infty) \uparrow \)
Sin extremos.

Por ejemplo, la función \(y=x^2\) representa una parábola, que es una curva en forma de U que se abre hacia arriba. Esta función tiene un valor mínimo en \(x=0\) y aumenta sin límite a medida que \(x\) se aleja de cero en cualquier dirección.
Cuando \(k\) es un entero negativo, la función representa el recíproco de un monomio. Por ejemplo, la función \(y = x^{-1} \) representa la función recíproca, también conocida como la función inversa. Esta función tiene una asíntota vertical en \(x=0\), donde la función se acerca a infinito positivo o negativo dependiendo del signo de \(x\). La función recíproca es simétrica respecto a la línea \(y=x\).
Cuando \(2k =n\) o \(2k+1 = n\) es una fracción, la función representa una función radical, donde el numerador de la fracción determina el grado de la raíz y el denominador determina la potencia de \(x\). Por ejemplo, la función \( y = x^\frac{1}{2} \) representa la función raíz cuadrada, que tiene un dominio de números reales no negativos y un rango de números reales no negativos. La función raíz cuadrada es una media parábola que se abre hacia la derecha y tiene una asíntota vertical en \(x=0\).
En general, la familia de funciones \(y=x^n\) exhibe una variedad de comportamientos dependiendo del valor de \(n\). La gráfica de estas funciones puede tener diferentes formas, incluyendo líneas, curvas y saltos discontinuos. El estudio de estas funciones es importante en matemáticas y ciencias, ya que aparecen en muchos fenómenos naturales y aplicaciones de ingeniería.

Algunas propiedades importantes de estas funciones incluyen:

• Cuando \(n\) es par, la función \(y=x^n\) siempre es no negativa para todos los valores reales de \(x\). Cuando \(n\) es impar, la función puede tomar valores positivos y negativos dependiendo del signo de \(x\).
• Cuando \(n\) es positivo, la función \(y=x^n\) es creciente en el intervalo \( (0, \infty) \) y decreciente en el intervalo \( (-\infty, 0) \). Cuando \(n\) es negativo, la función tiene el comportamiento opuesto.
• La derivada de la función \(y=x^n\) se da por \( y'=nx^{n-1} \). Esto significa que la pendiente de la recta tangente a la función en cualquier punto es proporcional al valor del exponente \(n\).
• La integral de la función \(y=x^n\) se da por \( \int x^n \, dx = \frac{x^{(n+1)}}{(n+1)} + C \), donde \(C\) es una constante de integración. Esta fórmula es válida para todos los valores de \(n\) excepto cuando \(n=-1\), en cuyo caso la integral se da por \( ln|x|+C \).

En resumen, la familia de funciones \(y=x^n\) es un tema fundamental en matemáticas, con muchas aplicaciones importantes en varios campos. El comportamiento y las propiedades de estas funciones dependen del valor del exponente \(n\), que determina la forma de la gráfica y otras características importantes.

Operaciones sobre funciones ☰

En matemáticas, las operaciones sobre funciones se refieren a operaciones matemáticas que se pueden realizar en funciones. Estas operaciones se pueden utilizar para manipular o combinar funciones para crear nuevas funciones. Las operaciones más comunes sobre funciones incluyen suma, resta, multiplicación, división, composición e inversa.

Suma y resta de funciones:
Las funciones se pueden sumar o restar para crear una nueva función. Dadas dos funciones \(f(x)\) y \(g(x)\), la suma o diferencia de las dos funciones se denota por \( (f \pm g)(x) \) y se define como:
\( (f+g) (x) = f(x)+ g(x) \)
\( (f-g) (x) = f(x)- g(x) \)
La suma de dos funciones pares es par, y la suma de dos funciones impares es impar.

Por ejemplo: \( f(x) = x+1 \) y \( g(x) = 2x-3 \) funciones.
\( \small (f+g) (x) = f(x) + g(x) = (x+1) + (2x-3) =\) \( 3x-2 \)
\( \small (f-g) (x) = f(x) - g(x) = (x+1) - (2x-3) =\) \( -x+4 \)

Multiplicación y división de funciones:
Las funciones también se pueden multiplicar o dividir para crear nuevas funciones. Dadas dos funciones \(f(x)\) y \(g(x)\), el producto o cociente de las dos funciones se denota por \( (f \cdot g) (x) \) o \( (\frac{f}{g}) (x) \) y se define como:
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( ( \frac{f}{g} )(x) = \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \)

El producto (cociente) de dos funciones pares y dos funciones impares es una función par, y el producto (cociente) de una función par y una función impar es una función impar.

Por ejemplo: \( f(x) = x+1 \) y \( g(x) = 2x-3 \) funciones.
\( (f \cdot g)(x) = (x+1)(2x-3) = 2x^2 - x - 3 \)
\( (\frac{f}{g})(x) = \frac{x+1}{2x-3} \)

Composición de funciones:
La composición de funciones es la operación de combinar dos o más funciones para crear una nueva función. Dadas dos funciones \( f(x) \) y \( g(x) \), la composición de las dos funciones se denota por \( (f \circ g)(x) \) y se define como: \( (f \circ g)(x) = f(g(x)) \).

Por ejemplo: \( f(x) = x^2 \) y \( g(x) = x+1 \) funciones.
\( (f \circ g) (x) = f(g (x) ) = f(x+1) = (x+1)^2 \)
Se nota que el orden de la composición importa, es decir, \( (f \circ g)(x) \) no es lo mismo que \( (g \circ f)(x) \).

Inversa de una función:
La inversa de una función es una nueva función que "deshace" la función original. Dada una función \(f(x) \), la inversa de la función se denota por \(f^{-1} (x) \) y se define como:
\( f^{-1} (f(x)) = x \)

Para que exista la inversa de una función, la función debe ser biyectiva. Una función es biyectiva si cada elemento en el dominio se asigna a un único elemento en el rango. La función inversa es la reflexión de la función a través de la línea \(y=x\).
Por ejemplo: Si \( f(x) = 2x+1 \), entonces \( f^{-1} (x) = \frac{x-1}{2} \)
Para verificar esto, podemos comprobar que \( f^{-1} (f(x))= \frac{2x+1-1}{2} = x \).

Aquí hay algunos detalles adicionales sobre las operaciones sobre funciones:

Propiedades de las operaciones sobre funciones:
Las operaciones sobre funciones tienen algunas propiedades que las hacen útiles para resolver problemas matemáticos. Estas propiedades incluyen:

• Asociatividad: El orden en el que se realizan las operaciones no afecta el resultado.
  Por ejemplo, \( (f+g)+h = f+(g+h) \)
• Conmutatividad: El orden de las funciones no afecta el resultado.
  Por ejemplo, \( f+g=g+f \)
• Distributividad: La operación se distribuye sobre otra operación.
  Por ejemplo, \( f \cdot (g+h) = f \cdot g + f \cdot h \)

Dominios y rangos:
Al realizar operaciones sobre funciones, es importante considerar los dominios y rangos de las funciones. El dominio de una función es el conjunto de valores para los cuales la función está definida, mientras que el rango es el conjunto de valores que la función puede tomar.
Al sumar o restar funciones, los dominios y rangos de las funciones deben ser iguales. Al multiplicar o dividir funciones, el dominio de la función resultante debe ser la intersección de los dominios de las dos funciones, y el rango de la función resultante puede estar restringido por el rango del denominador.
Al componer funciones, el rango de la función interna debe ser un subconjunto del dominio de la función externa.

Transformaciones de funciones:
Las operaciones sobre funciones también se pueden utilizar para transformar funciones. Por ejemplo, sumar una constante a una función desplaza la función verticalmente, mientras que multiplicar una función por una constante escala la función verticalmente. De manera similar, sumar una variable a una función desplaza la función horizontalmente, mientras que multiplicar una función por una variable escala la función horizontalmente.