Ecuaciones cuadráticas ☰

La forma general de una ecuación cuadrática es:
\(ax^2+bx+c=0\) , donde \(a≠0\), \(a\), \(b\) y \(c\) son constantes y \(x\) es la variable.
La ecuación cuadrática se puede resolver utilizando la fórmula cuadrática, que es:
\(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}\)
La fórmula cuadrática proporciona las soluciones para la ecuación cuadrática, que pueden ser reales o complejas, dependiendo del discriminante \((b^2–4ac)\). Si el discriminante es positivo, la ecuación cuadrática tiene dos raíces reales distintas. Si el discriminante es cero, la ecuación cuadrática tiene una raíz real, que es una raíz doble. Si el discriminante es negativo, la ecuación cuadrática tiene dos raíces complejas.

Ecuaciones cuadráticas incompletas:

Si al menos uno de los coeficientes de \(b\) y \(c\) en la ecuación cuadrática \(ax^2+bx+c=0\) es igual a cero, entonces la ecuación se llama ecuación cuadrática incompleta.

Resolución de ecuaciones cuadráticas ☰

Existen varios métodos para resolver ecuaciones cuadráticas, incluyendo:

• Factorización: Esto implica escribir la expresión cuadrática como un producto de dos binomios y establecer cada binomio igual a cero para encontrar las raíces de la ecuación.
• Completar el cuadrado: Esto implica manipular la expresión cuadrática en la forma de un trinomio cuadrado perfecto, y luego resolver las raíces usando álgebra básica.
• Fórmula cuadrática: Esta fórmula proporciona las raíces de cualquier ecuación cuadrática en términos de sus coeficientes, y puede ser derivada usando el método de completar el cuadrado.
• Graficación: Esto implica trazar la función cuadrática e identificar las intersecciones en \(x\), que corresponden a las raíces de la ecuación.
• Métodos numéricos: Hay varios métodos numéricos que se pueden utilizar para aproximar las raíces de una ecuación cuadrática, como el método de Newton, el método de bisección y el método de la secante.

Cada uno de estos métodos tiene sus ventajas y desventajas, y la elección del método depende del problema específico en cuestión y de las herramientas y recursos disponibles.


Método de Factorización de Ecuaciones Cuadráticas:
El método de factorización es una técnica utilizada para factorizar expresiones cuadráticas y resolver ecuaciones cuadráticas. Para factorizar una expresión cuadrática usando este método, necesitamos encontrar dos binomios que se multipliquen para dar la expresión cuadrática. La forma general de una expresión cuadrática es:
\(ax^2+bx+c\)

Para factorizar esta expresión cuadrática, podemos buscar dos binomios en la forma:
\((mx+r)(nx+s)\) , donde \(m\), \(n\), \(r\) y \(s\) son constantes. Expandiendo el producto de estos dos binomios, obtenemos:
\(mnx^2+(ms+rn)x+rs\).
Comparando esto con la forma general de la expresión cuadrática, podemos ver que:
\(mn=a\)
\(ms+rn=b\)
\(rs=c\)

Podemos usar estas ecuaciones para resolver para \(m, n, r\) y \(s\). Una vez que hemos encontrado estas constantes, podemos escribir la expresión cuadrática en forma factorizada como:
\(ax^2+bx+c=(mx+r)(nx+s) \).
Para resolver una ecuación cuadrática usando el método de factorización, primero podemos factorizar la expresión cuadrática como se muestra arriba. Una vez que hemos factorizado la expresión cuadrática, podemos usar la propiedad del producto cero para encontrar las raíces de la ecuación. La propiedad del producto cero establece que si el producto de dos factores es cero, entonces al menos uno de los factores debe ser cero. Por lo tanto, si hemos factorizado la expresión cuadrática como:
\((mx+r)(nx+s)=0\), entonces podemos establecer cada factor igual a cero y resolver para \(x\):
\((mx+r)=0 \) o \((nx+s) =0\)
Resolviendo cada ecuación lineal, obtenemos:
\(x=-\frac{r}{m}\) o \(x=-\frac{s}{n}\)
Por lo tanto, las raíces de la ecuación cuadrática son \(x=-\frac{r}{m}\) o \(x=-\frac{s}{n}\).
Vale la pena señalar que no todas las expresiones cuadráticas se pueden factorizar usando números reales. En tales casos, es posible que necesitemos usar otros métodos como completar el cuadrado o la fórmula cuadrática para encontrar las raíces de la ecuación.

Ejemplo:
Supongamos que tenemos la ecuación cuadrática: \(x^2-5x+6=0\).
Para resolver esta ecuación usando el método de factorización, necesitamos factorizar la expresión cuadrática \( x^2–5x+6 \) en un producto de dos binomios. Podemos buscar dos binomios en la forma:
\((mx+r)(nx+s)\), donde \(m\), \(n\), \(r\) y \(s\) son constantes. Expandiendo el producto de estos dos binomios, obtenemos:
\(mnx^2+(ms+rn)x+rs\).
Comparando esto con la expresión cuadrática \( x^2 –5x+6 \), podemos ver que:
\(mn=1 \)
\(ms+rn=-5 \)
\(rs=6 \)
Podemos intentar diferentes valores de \(m\), \(n\), \(r\) y \(s\) hasta que encontremos valores que satisfagan estas ecuaciones.
Un posible conjunto de valores es \(m=1\), \(n=1\), \(r=-2\) y \(s=-3\) que dan:
\((mx+r)(nx+s) \)
\((x-2)(x-3)=0 \)
Por lo tanto, las raíces de la ecuación cuadrática son \(x=2\) y \(x=3\)
Podemos verificar que estos valores son realmente raíces de la ecuación cuadrática sustituyéndolos en la ecuación original
\(2^2-5\cdot 2+6=0 \)
\(3^2-5\cdot 3+6=0 \)
Ambas de estas ecuaciones son verdaderas, entonces \(x=2\) y \(x=3\) son de hecho raíces de la ecuación cuadrática.

Completando el cuadrado:
Primero necesitamos escribir la expresión cuadrática en forma de un cuadrado completo. Un cuadrado completo es una expresión de la forma \((x+a)^2=x^2+2ax+a^2\), donde \(a\) es una constante. Cualquier expresión cuadrática se puede escribir en forma de un cuadrado completo sumando o restando una constante.
Supongamos que tenemos una ecuación cuadrática de la forma: \(ax^2+bx+c=0\)
Para resolver esta ecuación dividiendo un cuadrado completo, primero escribimos la expresión cuadrática como un cuadrado completo sumando o restando una constante. Podemos hacer esto completando el cuadrado de la siguiente manera:

\( a(x^2 + \frac{b}{a}x) = -c \)

\(a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) = -c + a(\frac{b^2}{4a^2})\)

\(a\left(x + \frac{b}{2a}\right)^2 = \frac{4ac - b^2}{4a}\)

Ahora podemos resolver para \(x\) dividiendo ambos lados por el coeficiente del término cuadrático:

\((x + \frac{b}{2a})^2 = \frac{4ac - b^2}{4a^2}\)

\(x + \frac{b}{2a} = \sqrt{\frac{4ac - b^2}{4a^2}}\)

\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Esta es la fórmula cuadrática, que da las raíces de cualquier ecuación cuadrática de la forma \( ax^2 + bx + c = 0 \)
También podemos usar la fórmula cuadrática para comprobar si una expresión cuadrática Si el discriminante \( b^2 –4ac \) es un cuadrado perfecto, entonces la expresión cuadrática se puede escribir en forma de un cuadrado completo. Si el discriminante no es un cuadrado perfecto, entonces la expresión cuadrática no se puede escribir en forma de un cuadrado completo.

Ejemplo:
Consideremos la ecuación cuadrática:
\(x^2+6x+1=0\).
Para completar el cuadrado, queremos reescribir la ecuación en la forma de \((x+a)^2+b\), donde \(a\) y \(b\) son constantes.
Primero, sumaremos y restaremos \((\frac{b}{2})^2\) \( ( (\frac{6}{2})^2 =9 ) \) al lado izquierdo de la ecuación para obtener:
\(x^2+6x+9-9+1=0\)
Observamos que los tres primeros términos del lado izquierdo forman un trinomio cuadrado perfecto, que podemos escribir como \((x+3)^2\)
Así que podemos reescribir la ecuación como: \((x+3)^2-8=0\)
Ahora podemos resolver para \(x\) sumando 8 a ambos lados y tomando la raíz cuadrada:
\((x+3)^2=8 \)
\(x+3=\pm \sqrt{8} \)
\(x=-3 \pm \sqrt{8} \)
Entonces, las soluciones de la ecuación original son:
\(x=-3+ \sqrt{8} \) y \(x=-3- \sqrt{8} \)
¡Y así es como se completa el cuadrado de una ecuación cuadrática!

Gráficos:
Graficar es un método visual para resolver ecuaciones cuadráticas. La idea detrás de este método es graficar la ecuación cuadrática e identificar los \(x\)-interceptos, que corresponden a las soluciones de la ecuación.
Si \(a > 0\), la parábola se abre hacia arriba, si \(a < 0\), la parábola se abre hacia abajo.
Para graficar una ecuación cuadrática, primero la reescribimos en la forma \( y=ax^2 +bx+c \), donde \(y\) es la variable dependiente y \(x\) es la variable independiente. El gráfico de una ecuación cuadrática es una parábola, que es una curva en forma de U. La dirección y forma de la parábola dependen del signo del coeficiente \(a\). Si \( a > 0 \), la parábola se abre hacia arriba, y si \( a < 0 \), la parábola se abre hacia abajo.
Para encontrar los \(x\)-interceptos de la parábola, establecemos \(y=0\) y resolvemos para \(x\). Esto nos da los valores de \(x\) donde la parábola interseca el eje \(x\). Estos valores corresponden a las soluciones de la ecuación cuadrática.

Consideremos un ejemplo para ilustrar este método. Supongamos que queremos resolver la ecuación cuadrática: \(x^2-4x-5=0\).
Podemos reescribir esta ecuación en la forma \( y=x^2 –4x-5 \) Para graficar la parábola, podemos usar una calculadora gráfica o un programa de software, o podemos dibujarla a mano.

Gráfico:


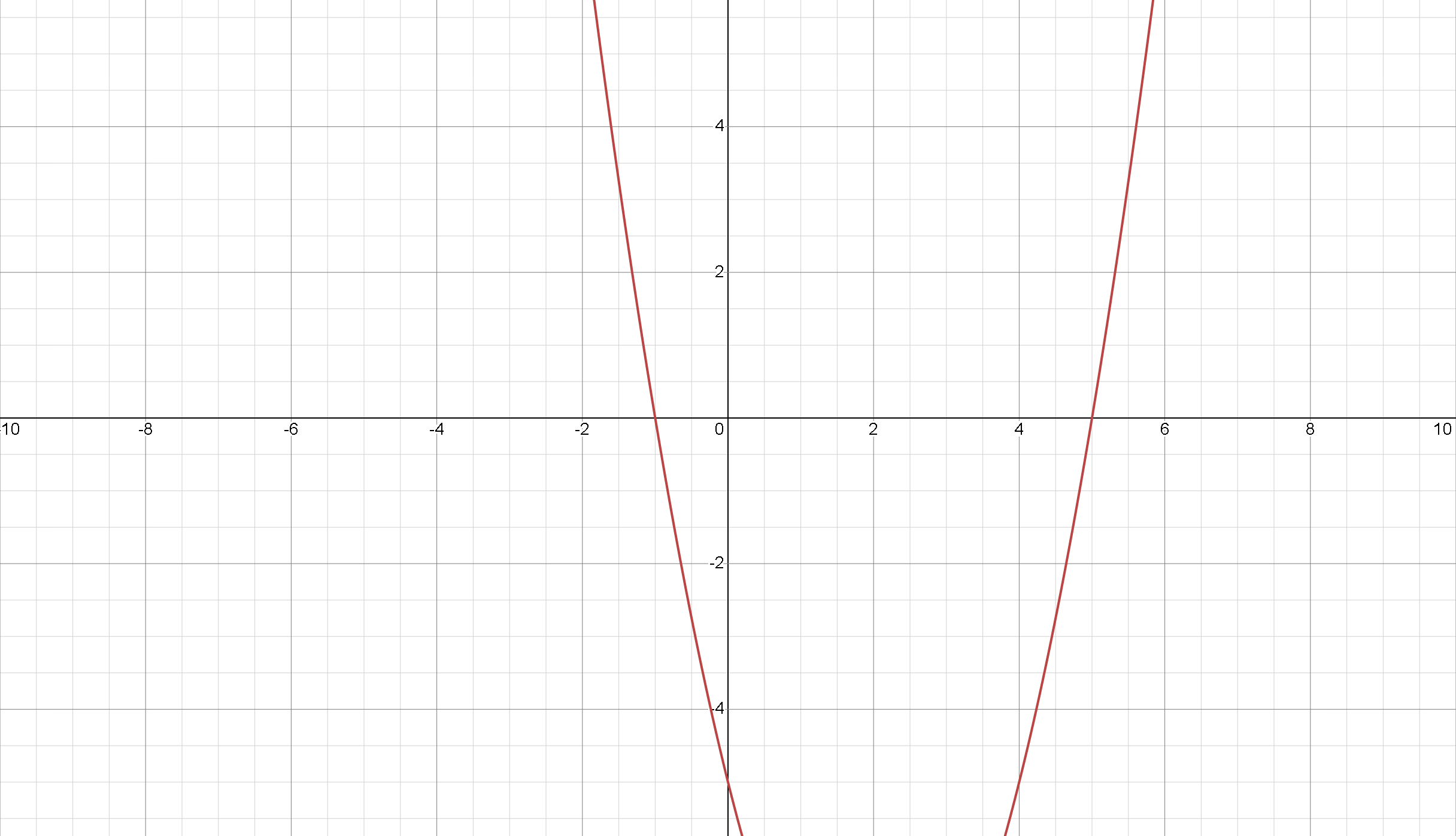
Podemos ver que la parábola interseca el eje \(x\) en dos puntos, que corresponden a las soluciones de la ecuación. Para encontrar estos puntos, podemos usar la fórmula cuadrática o estimar los valores de \(x\) a partir del gráfico. En este caso, los \(x\)-interceptos son aproximadamente \(x=-1\) y \(x=5\), que son las soluciones de la ecuación cuadrática.

En resumen, graficar es un método útil para resolver ecuaciones cuadráticas visualmente. Al graficar la ecuación e identificar los \(x\)-interceptos, podemos encontrar rápidamente las soluciones de la ecuación.

Fórmula cuadrática ☰

La fórmula para las raíces de una ecuación cuadrática de la forma \(ax^2+bx+c=0\) se conoce como la fórmula cuadrática. Se da por:

\(x =\frac{-b \pm \sqrt{b^2- 4ac}}{2a}\)

Esta fórmula nos da los valores de \(x\), que son las raíces o soluciones de la ecuación cuadrática. El símbolo \( \pm \) significa que necesitamos encontrar tanto las raíces positivas como negativas. La expresión dentro de la raíz cuadrada, \( (b^2 – 4ac) \), se llama el discriminante de la ecuación cuadrática, y nos dice cuántas raíces reales tiene la ecuación.

Si el discriminante es positivo \( (b^2 –4ac > 0) \), la ecuación cuadrática tiene dos raíces reales distintas, dadas por la fórmula anterior.

Si el discriminante es cero \( (b^2 –4ac=0) \), la ecuación cuadrática tiene una raíz real, que se da por \(x=-\frac{b}{2a}\)

Si el discriminante es negativo \( (b^2 – 4ac < 0) \), la ecuación cuadrática tiene dos raíces complejas, que se dan por:

\(x =\frac{-b \pm i\sqrt{4ac-b^2}}{2a}\) ,

donde \(i\) es la unidad imaginaria, igual a la raíz cuadrada de \(-1\).
La fórmula cuadrática es una herramienta poderosa para resolver ecuaciones cuadráticas, y se puede utilizar para cualquier ecuación cuadrática, independientemente de los valores de los coeficientes \(a\), \(b\) y \(c\).

Teorema de Viète ☰

El teorema de Viète, también conocido como las fórmulas de Vieta o las relaciones de Vieta, es un teorema fundamental en álgebra que relaciona los coeficientes de un polinomio con las sumas y productos de sus raíces. El teorema lleva el nombre del matemático francés François Viète (latinizado como Franciscus Vieta), quien lo descubrió por primera vez en el siglo XVI.

Más específicamente, el teorema de Viète establece que para un polinomio de grado \( n \) con coeficientes \( a_n, a_{n-1},…, a_1, a_0 \) y raíces \( r_1, r_2,…, r_n \), se cumplen las siguientes relaciones: La suma de las raíces es igual al cociente del coeficiente opuesto y el coeficiente principal:
\( r_1+r_2+ … +r_n=-\frac{a_{n-1}}{a_n} \)

La suma de los productos de las raíces tomadas de dos en dos es igual al cociente del término constante y el coeficiente principal con un cambio de signo según la paridad de \( n \): $$ r_1 r_2+r_1 r_3+ … +r_{n-1}r_n=(-1)^n \cdot \frac{a_0}{a_n} $$

La suma de los productos de las raíces tomadas de tres en tres es igual al cociente del coeficiente de la potencia penúltima y el coeficiente principal con un cambio de signo según la paridad de \( n \): $$ r_1 r_2 r_3+r_1 r_2 r_4+ … +r_{n-2} r_{n-1} r_n=(-1)^{n-1} \cdot \frac{a_{n-2}}{a_n} $$

y así sucesivamente, con la suma de los productos de las raíces tomadas de \( k \) en \( k \) siendo igual a
\( (-1)^{n-k} \cdot \frac{a_{n-k}}{a_n} \) para \( k = 1,2,…,n \).

Estas relaciones son útiles para resolver ecuaciones que involucran raíces polinomiales, ya que permiten expresar los coeficientes de un polinomio en términos de sus raíces y viceversa.

El teorema de Viète se puede aplicar a ecuaciones cuadráticas, que son polinomios de grado 2. Para una ecuación cuadrática de la forma \(ax^2+bx+c=0\), las raíces se pueden encontrar usando la fórmula cuadrática:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)

Usando el teorema de Viète, podemos relacionar las raíces de la ecuación cuadrática con sus coeficientes de la siguiente manera:

La suma de las raíces es igual al opuesto del coeficiente de \(x\) dividido por el coeficiente de \(x^2\):
\( r1+r2=- \frac{b}{a} \)

El producto de las raíces es igual al término constante dividido por el coeficiente de \(x^2\):
\( r1 \cdot r2= \frac{c}{a} \)

Estas relaciones se pueden derivar expandiendo la ecuación cuadrática usando la propiedad distributiva y comparando la expresión resultante con la forma estándar de una ecuación cuadrática.

Por ejemplo, supongamos que tenemos la ecuación cuadrática \( x^2+5x+6=0 \). Usando la fórmula cuadrática, podemos encontrar las raíces como -2 y -3. Usando el teorema de Viète, podemos verificar que estos valores satisfacen las relaciones:
\( -2+(-3)= -\frac{5}{1} \), que es el opuesto del coeficiente de \(x\) (5) dividido por el coeficiente de \(x^2\) (1).
\( -2 \cdot (-3)= \frac{6}{1} \), que es el término constante (6) dividido por el coeficiente de \(x^2\) (1).

Estas relaciones se mantienen para todas las ecuaciones cuadráticas y son útiles para resolver problemas que implican encontrar las raíces de una ecuación cuadrática o expresar los coeficientes de una ecuación cuadrática en términos de sus raíces.

Las ecuaciones cuadráticas se pueden usar para resolver una amplia gama de problemas en varios campos, como física, ingeniería, finanzas y más. Aquí hay algunos ejemplos de resolución de problemas usando ecuaciones cuadráticas:

• Movimiento de proyectiles: Un proyectil lanzado desde el suelo con una velocidad inicial \(v_0\) y un ángulo \(\theta\) sigue una trayectoria parabólica descrita por la ecuación \( y = -\frac{1}{{2g\left(\frac{x}{v_0\cos\theta}\right)^2}} + x\tan\theta \), donde \(g\) es la aceleración debido a la gravedad. Esta ecuación se puede reescribir como una ecuación cuadrática en \(x\), que se puede usar para determinar la distancia horizontal recorrida por el proyectil, la altura máxima alcanzada y el tiempo de vuelo.
• Optimización cuadrática: En muchos problemas de optimización, la función objetivo se puede expresar como una ecuación cuadrática, como \( f(x)=ax^2+bx+c \), donde \(a > 0\). Para encontrar el valor máximo o mínimo de la función, podemos usar la fórmula del vértice, que da la coordenada \(x\)- del vértice como \( -\frac{b}{2a} \) y la coordenada \(y\) correspondiente como \(f ( -\frac{b}{2a} ) \)
• Negocios y finanzas: En los negocios y las finanzas, las ecuaciones cuadráticas se pueden usar para modelar diversas situaciones, como la maximización de ganancias y ingresos, la minimización de costos y el análisis de punto de equilibrio. Por ejemplo, la función de ganancias para un producto se puede expresar como \(P(x)=-ax^2+bx-c \), donde \(x\) es el número de unidades vendidas y \(a\), \(b\) y \(c\) son constantes. Para encontrar el nivel de producción que maximiza la ganancia, podemos usar la fórmula cuadrática para determinar el valor de \(x\) que maximiza \(P(x)\)
• Ingeniería: En ingeniería, las ecuaciones cuadráticas se pueden usar para modelar y resolver diversos problemas, como determinar la frecuencia natural de un sistema vibratorio, el diseño óptimo de una estructura o máquina y la trayectoria de un vehículo o misil. Por ejemplo, la frecuencia natural de un sistema vibratorio se puede expresar como \( \omega = \sqrt{\frac{k}{m}}\) , donde \(k\) es la constante del resorte y \(m\) es la masa del sistema. Esta ecuación se puede reorganizar para dar una ecuación cuadrática en \( \omega ^2 \), que se puede resolver para determinar la frecuencia natural.

Estos son solo algunos ejemplos de resolución de problemas usando ecuaciones cuadráticas. En general, las ecuaciones cuadráticas se pueden usar para modelar y resolver una amplia gama de problemas, y son una herramienta poderosa en muchos campos de estudio.