Inecuaciones cuadráticas
Una inecuación cuadrática es un tipo de desigualdad en la que aparece una función cuadrática. Las inecuaciones cuadráticas tienen la forma:
\( ax^2 + bx + c,,,,op,,,,0 \), donde \(a\), \(b\) y \(c\) son números reales y \(op\) es uno de los símbolos de desigualdad \( < \), \( \le \), \(> \) o \( \ge \).
La solución a una inecuación cuadrática es el conjunto de todos los valores de \(x\) que satisfacen la desigualdad. Para encontrar el conjunto de soluciones, podemos seguir los siguientes pasos:
- Resolver la ecuación cuadrática correspondiente \( ax^2 + bx + c = 0 \) para encontrar las raíces de la función cuadrática.
- Graficar la función cuadrática en un plano de coordenadas.
- Determinar la región o regiones del gráfico que están por encima o por debajo del eje \(x\), dependiendo del signo de \(a\).
- Colorear la(s) región(es) apropiada(s) del gráfico, dependiendo del símbolo de desigualdad.
- Escribir el conjunto de soluciones utilizando notación de intervalos o notación de conjuntos.
Veamos algunos ejemplos:
Ejemplo 1:
Resolver la desigualdad \(x^2 - 4x + 3 \ge 0\).
Solución: Primero, encontramos las raíces de la ecuación cuadrática correspondiente \(x^2 - 4x + 3 = 0\) factorizando o usando la fórmula cuadrática:
\( x^2 - 4x + 3 = (x-1)(x-3)=0 \).
Por lo tanto, las raíces son \( x=1 \) y \(x=3\).
Luego, graficamos la función cuadrática \( f(x) = x^2 - 4x + 3 \).
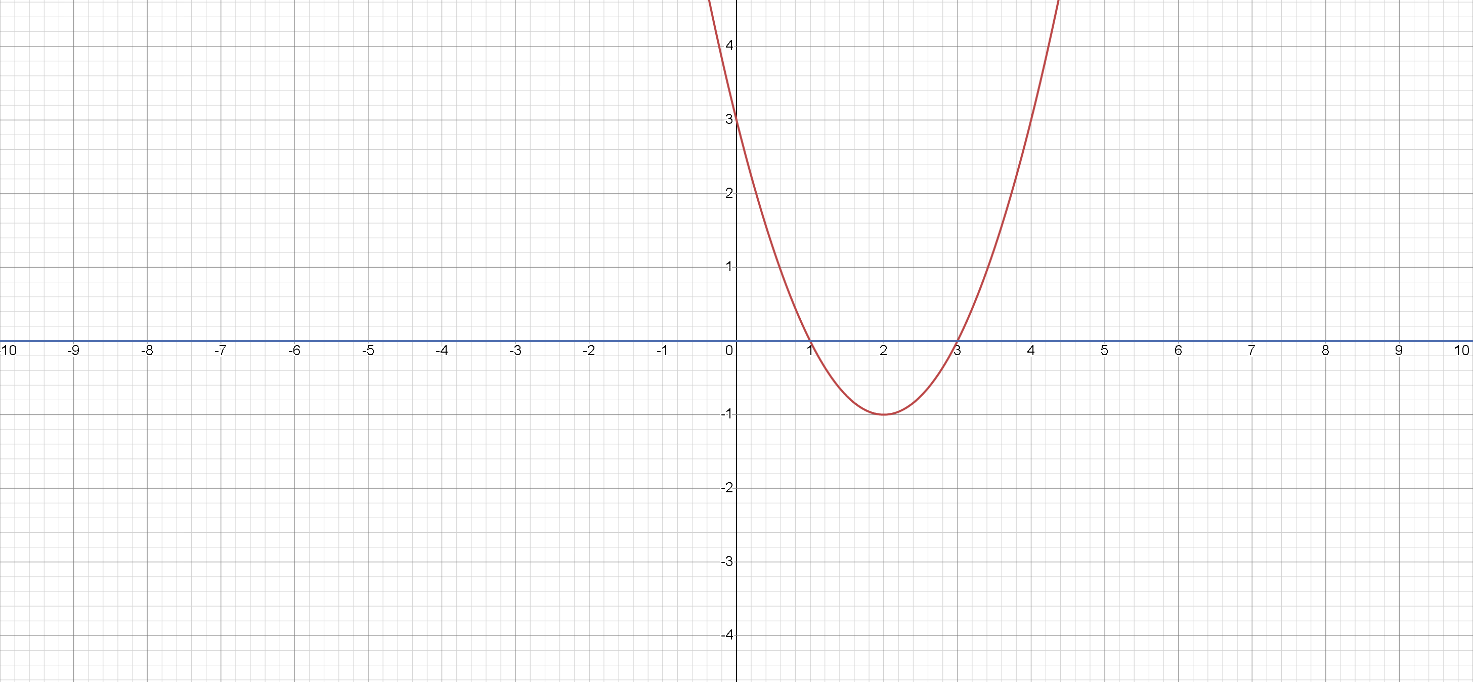
Podemos ver que el gráfico de la función está por encima del eje \(x\) entre las raíces \(x=1\) y \(x=3\).
Por lo tanto, la solución de la desigualdad \( x^2 - 4x + 3 \ge 0 \) es: \( x \in (-\infty, 1] \cup [3, \infty) \).
Ejemplo 2: Un ejemplo de resolver una inecuación cuadrática usando el método de intervalos.
Consideremos la desigualdad: \( 2x^2 - 5x - 3 < 0 \).
Para resolver esta desigualdad, primero encontramos las raíces de la ecuación cuadrática \( 2x^2-5x-3=0 \)
\( x=-\frac{1}{2} \) y \( x = 3 \). Podemos encontrar estas raíces factorizando el cuadrático o usando la fórmula cuadrática.
Luego, usamos las raíces para dividir la recta numérica en tres intervalos:
\( (-\infty ; -\frac{1}{2} ) \), \( (-\frac{1}{2}; 3) \) y \( (3; \infty)\).
Luego, probamos un valor de cada intervalo en la desigualdad para determinar si es verdadera o falsa en ese intervalo.
Para el intervalo \( (-\infty ; -\frac{1}{2}) \) podemos elegir \( x= -1 \) como valor de prueba.
Sustituyendo \(x=-1\) en la desigualdad, obtenemos: \( 2(-1)^2 - 5(-1) - 3 < 0 \), que se simplifica a: \( 4 < 0 \).
Esto es falso, por lo que la desigualdad no se cumple en el intervalo \( (-\infty ; -\frac{1}{2}) \) .
Para el intervalo \( (-\frac{1}{2} ; 3) \) podemos elegir \(x=0\) como valor de prueba.
Sustituyendo \(x=0\) en la desigualdad, obtenemos: \( 2(0)^2 - 5(0) - 3 < 0 \), que se simplifica a: \( -3 < 0 \).
Esto es verdadero, por lo que la desigualdad se cumple en el intervalo \( (-\frac{1}{2} ; 3) \).
Para el intervalo \( (3; \infty) \) podemos elegir \(x=4\) como valor de prueba.
Sustituyendo \(x=4\) en la desigualdad, obtenemos: \(2(4)^2 - 5(4) - 3 < 0 \), que se simplifica a: \( 5 < 0 \).
Esto es falso, por lo que la desigualdad no se cumple en el intervalo \( (3;\infty) \).
Por lo tanto, la solución de la desigualdad \( 2x^2-5x-3 < 0 \) es: \( x\ \in (-\frac{1}{2} ; 3) \)
Esto significa que cualquier valor de \(x\) que sea mayor que \(-\frac{1}{2}\) y menor que \(3\) hace que la desigualdad sea verdadera.
Resolviendo desigualdades racionales mediante el método de intervalos
Para resolver desigualdades racionales mediante el método de intervalos, sigue estos pasos:
- Rewrite la desigualdad como una única expresión racional, con cero en un lado y el otro lado en una fracción.
- Determina los valores críticos de la expresión encontrando dónde el numerador y el denominador son iguales a cero.
- Divide la recta numérica en intervalos separados por los valores críticos encontrados en el paso 2.
- Determina el signo de la expresión en cada intervalo e identifica los intervalos donde la expresión es positiva o negativa.
- Escribe la solución en notación de intervalos, utilizando los intervalos donde la expresión es positiva o negativa, dependiendo de la dirección de la desigualdad.
Por ejemplo, vamos a resolver la desigualdad \(\frac{2x-5}{x+1} > 1 \) mediante el método de intervalos.
1. Rewrite la desigualdad como una única expresión racional:
\(\frac{2x-5}{x+1} -1 > 0 \)
Simplifica el lado izquierdo y combina términos semejantes:
\( \frac{2x-5-(x+1)}{x+1} > 0 \)
\( \frac{x-6}{x+1} \)
2. Determina los valores críticos estableciendo el numerador y el denominador igual a cero:
\( x-6=0 \rightarrow x=6 \).
\( x+1=0 \rightarrow x=-1 \).
3. Divide la recta numérica en intervalos:
\( (-\infty ; -1) \), \( (-1;6) \), \( (6;\infty ) \).
4. Determina el signo de la expresión en cada intervalo probando un punto en cada intervalo:
Para \( x=-2 \), \( \frac{-2-6}{-2+1} = 8 > 0 \), así que la expresión es positiva en \( (-\infty ; -1) \).
Para \( x = 0 \), \( \frac{0-6}{0+1} = -6 < 0 \), así que la expresión es negativa en \( (-1 ; 6 ) \).
Para \( x = 7 \), \( \frac{7-6}{7+1} = \frac{1}{8} > 0 \), así que la expresión es positiva en \( (6; \infty ) \).
5. Escribe la solución en notación de intervalos:
La desigualdad es verdadera donde la expresión es positiva, así que la solución es \( x \in (- \infty ; -1 ) \cup (6; \infty ) \).
Inecuaciones irracionales
Una inecuación irracional es una desigualdad que involucra una o más expresiones irracionales, como raíces cuadradas o raíces cúbicas. El proceso para resolver una inecuación irracional es diferente al de resolver una desigualdad regular, porque elevar al cuadrado o elevar a una potencia puede introducir soluciones extranjeras. Para resolver una inecuación
irracional, necesitas aislar la expresión irracional en un lado de la desigualdad, y luego elevar al cuadrado o elevar ambos lados de la desigualdad para eliminar la raíz. Sin embargo, al hacer esto, puedes introducir soluciones que no son válidas para la desigualdad original, porque elevar al cuadrado o elevar a una potencia puede cambiar el signo de un número. Por
lo tanto, necesitas verificar tus soluciones para asegurarte de que sean válidas para la desigualdad original.
Para resolver inecuaciones irracionales, sigue estos pasos generales:
1. Aisla la expresión irracional en un lado de la desigualdad.
2. Eleva al cuadrado ambos lados de la desigualdad (o eleva ambos lados a una potencia que elimine la raíz).
3. Resuelve la desigualdad resultante.
4. Verifica las soluciones para la desigualdad original, ya que elevar al cuadrado o elevar a una potencia puede introducir soluciones extranjeras.
Por ejemplo, resolvamos la desigualdad \( \sqrt{2x-1} > 3 \) .
1. Eleva al cuadrado ambos lados de la desigualdad:
\( (\sqrt{2x-1})^2 > 3^2 \rightarrow 2x - 1 > 9 \)
2. Resuelve la desigualdad resultante:
\( 2x > 10 \rightarrow x > 5 \) .
\( \small \sqrt{2x-1} > 3 \rightarrow 2x > 10 \rightarrow x > 5 \)
3. Verifica la solución para la desigualdad original:
Sustituye \(x=6\) en la desigualdad original:
\( \sqrt{2(6)-1} > 3 \rightarrow \sqrt{11} > 3 \)
Esto es verdadero, entonces \(x=6\) es una solución válida para la desigualdad.
Sustituye \(x=4\) en la desigualdad original:
\( \sqrt{2(4)-1} > 3 \rightarrow \sqrt{7} > 3 \)
Esto es falso, entonces \(x=4\) no es una solución válida para la desigualdad.
Por lo tanto, la solución es \(x > 5\).
Nota: Siempre ten en cuenta que la expresión de la raíz no puede ser un número negativo.