Ángulo de rotación
El ángulo de rotación es un concepto utilizado en geometría para describir la cantidad de rotación aplicada a una figura alrededor de un punto fijo llamado centro de rotación. Cuando una figura se rota, todos los puntos de la figura se mueven a lo largo de trayectorias circulares alrededor del centro de rotación, y el ángulo de rotación es la cantidad de rotación,
medida en grados o radianes, que experimenta la figura.
Para definir el ángulo de rotación matemáticamente, necesitamos usar el concepto del círculo unitario. El círculo unitario es un círculo centrado en el origen del plano cartesiano con un radio de 1. Podemos usar el círculo unitario para definir las funciones seno y coseno de un ángulo, que son funciones trigonométricas fundamentales.
Supongamos que tenemos un punto \((x,y) \) en el círculo unitario que forma un ángulo de \( \theta \) con el eje \(x\) positivo, como se muestra en la figura a continuación:
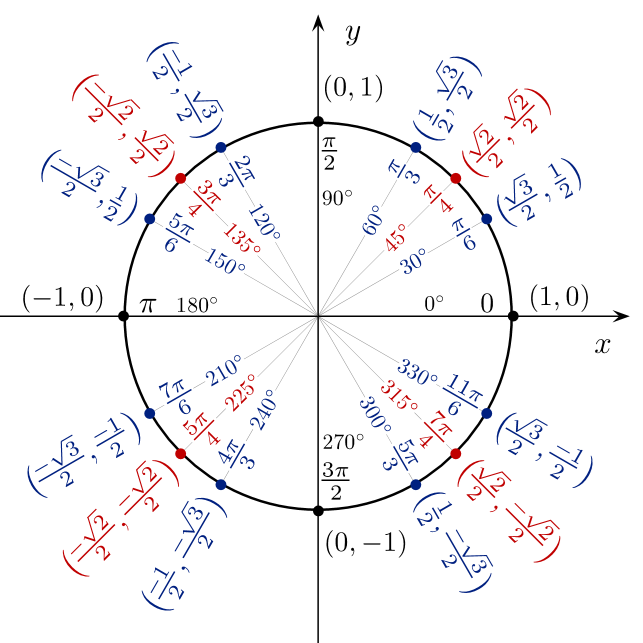
Entonces las coordenadas del punto están dadas por:
\( x = \cos( \theta ) \), \( y = \sin( \theta) \).
El ángulo de rotación se puede definir de la siguiente manera. Supongamos que tenemos una figura \(F\) en el plano, y rotamos la figura en sentido antihorario alrededor de un punto fijo \(O\) por un ángulo de \( \theta \). Sea \(F' \) la imagen de \(F\) bajo esta rotación. Entonces el ángulo de rotación se define como el ángulo entre dos segmentos de línea
correspondientes de \(F \) y \(F' \), ambos de los cuales intersectan en el centro de rotación \(O\).
Podemos expresar el ángulo de rotación en términos de las coordenadas de los puntos en el círculo unitario. Supongamos que tenemos un punto \(P=(x,y) \) en \(F\) que rota en sentido antihorario alrededor de \(O\) por un ángulo de \( \theta \), y sea \(P'=(x',y' ) \) el punto correspondiente en \(F' \). Entonces el ángulo de rotación se puede calcular utilizando la
siguiente fórmula:
\( \theta = \cos^{-1}\left(\frac{xx' + yy'}{\sqrt{x^2 + y^2} \sqrt{{x'}^2 + {y'}^2}}\right) \)
Esta fórmula se deriva de la fórmula del producto punto para el ángulo entre dos vectores. El numerador de la fracción es el producto punto de los vectores \(OP\) y \(OP'\), y el denominador es el producto de sus magnitudes.
En resumen, el ángulo de rotación es una medida de la cantidad de rotación aplicada a una figura alrededor de un punto fijo, y se puede calcular utilizando la fórmula del producto punto o midiendo el ángulo entre segmentos de línea correspondientes de las figuras original y rotada.
Medida en Grados y Radianes
Un ángulo es una figura geométrica formada por dos rayos o segmentos de línea que comparten un punto común llamado vértice. Los ángulos pueden medirse en diferentes unidades, pero las unidades más comunes son los radianes y los grados.
Los radianes son una unidad de medida angular que se basa en la longitud de un arco de un círculo. Un radián se define como el ángulo que subtende un arco de longitud igual al radio del círculo. En otras palabras, si un círculo tiene un radio \( r \), entonces un ángulo de un radián en el centro del círculo subtenderá un arco de longitud \( r \). El símbolo para los
radianes es "rad".
Los grados son otra unidad de medida angular que se basa en dividir un círculo en 360 partes iguales, siendo cada parte un grado. El símbolo para los grados es "\( \circ \)". Una vuelta completa alrededor de un círculo es equivalente a 360 grados \( (360^\circ ) \).
Para convertir entre radianes y grados, podemos usar las siguientes fórmulas:
- Para convertir de radianes a grados: multiplicar el ángulo por \( \frac{180}{\pi} \).
- Para convertir de grados a radianes: multiplicar el ángulo por \( \frac{\pi}{180} \).
Por ejemplo, supongamos que tenemos un ángulo de \( \theta = 2 \text{ radianes}\). Para convertir este ángulo a grados, podemos usar la fórmula:
\( \theta = \text{radianes} \cdot \frac{180}{\pi} = 2 \cdot \frac{180}{\pi} \approx 114.59^\circ \)
De manera similar, supongamos que tenemos un ángulo de \( \theta = 45^\circ \). Para convertir este ángulo a radianes, podemos usar la fórmula:
\( \theta = \text{grados} \cdot \frac{\pi}{180} = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ rad} \)
En resumen, los radianes y los grados son dos unidades comunes de medida angular utilizadas para medir ángulos en geometría. Los radianes se basan en la longitud de un arco de un círculo, mientras que los grados se basan en dividir un círculo en 360 partes iguales. Podemos convertir entre radianes y grados usando las fórmulas mencionadas anteriormente.
Funciones Trigonométricas y el Círculo Unitario
Las funciones trigonométricas son funciones matemáticas que relacionan los ángulos de un triángulo con las longitudes de sus lados. Las funciones trigonométricas más comúnmente utilizadas son el seno, el coseno y la tangente. Estas funciones suelen representarse utilizando el círculo unitario, que es un círculo con un radio de 1 centrado en el origen de un sistema
de coordenadas cartesianas.
El círculo unitario es útil porque nos permite visualizar fácilmente las relaciones entre los ángulos y las funciones trigonométricas. Si trazamos una línea desde el origen hasta un punto en el círculo unitario, el ángulo entre esa línea y el eje x positivo se conoce como el ángulo de rotación o simplemente el ángulo. El punto donde la línea interseca el círculo
unitario corresponde a un valor específico de seno, coseno y tangente.
Aquí están las definiciones de las tres principales funciones trigonométricas:
- Seno (sin): la razón entre la longitud del lado opuesto al ángulo y la longitud de la hipotenusa de un triángulo rectángulo.
- Coseno (cos): la razón entre la longitud del lado adyacente al ángulo y la longitud de la hipotenusa de un triángulo rectángulo.
- Tangente (tan): la razón entre la longitud del lado opuesto al ángulo y la longitud del lado adyacente al ángulo de un triángulo rectángulo.
Utilizando el círculo unitario, también podemos definir las otras tres funciones trigonométricas: cosecante (csc), secante (sec) y cotangente (cot). Estas son simplemente los recíprocos del seno, coseno y tangente, respectivamente.
Las funciones seno, tangente y cotangente son impares, y el coseno es una función par.
Funciones Trigonométricas de Cualquier Ángulo
Las funciones trigonométricas pueden definirse para cualquier ángulo, no solo para ángulos en triángulos rectángulos. Las definiciones de las funciones trigonométricas de un ángulo en un círculo unitario se dan a continuación:
Consideremos un ángulo \( \theta \) en posición estándar, lo que significa que comienza desde el eje \( x \) positivo y gira en sentido contrario a las agujas del reloj.
Sea \( (x, y) \) el punto donde el lado terminal del ángulo \( \theta \) interseca el círculo unitario centrado en el origen.
Seno (sin): \( \sin(\theta) = y \)
Coseno (cos): \( \cos(\theta) = x \)
Tangente (tan): \( \tan(\theta) = \frac{y}{x} \), \(x \neq 0 \)
Las otras tres funciones trigonométricas se pueden definir de la siguiente manera:
Cosecante (csc): \( \csc(\theta) = \frac{1}{\sin(\theta)} \)
Secante (sec): \( \sec(\theta) = \frac{1}{\cos(\theta)} \)
Cotangente (cot): \( \cot(\theta) = \frac{1}{\tan(\theta)} \)
Los valores de las funciones trigonométricas pueden ser positivos, negativos o cero, dependiendo del cuadrante en el que se encuentre el ángulo \( \theta \). En el primer cuadrante \( (0 < \theta < 90 \text{ grados}) \), todas las seis funciones trigonométricas son positivas. En el segundo cuadrante \( (90 < \theta < 180 \text{ grados}) \), solo el seno es positivo.
En el tercer cuadrante \( (180 < \theta < 270 \text{ grados}) \), solo la tangente es positiva. En el cuarto cuadrante \( (270 < \theta < 360 \text{ grados}) \), solo el coseno es positivo.
Ten en cuenta que los ángulos pueden medirse en grados o radianes. Los radianes son otra forma de medir los ángulos, donde un radian se define como el ángulo que subtiende un arco de longitud igual al radio del círculo. La conversión entre grados y radianes se da por:
\( \pi \text{ radianes} = 180 \text{ grados} \)
\( \text{1 radianes} \approx 57.3 \text{ grados} \)
\( \text{1 grados} \approx 0.0175 \text{ radianes} \)
Cuando trabajamos con funciones trigonométricas de ángulos medidos en radianes, usamos la letra griega \( \pi \) (pi) como una forma conveniente de expresar estos ángulos. Por ejemplo, un ángulo de 90 grados se puede expresar como \( \frac{\pi}{2} \) radianes, y un ángulo de 180 grados se puede expresar como \( \pi \) radianes.
También podemos usar identidades trigonométricas para simplificar expresiones trigonométricas. Por ejemplo, la identidad pitagórica establece que \( \sin^2(\theta)+\cos^2(\theta)=1 \), que es verdadera para todos los valores de \( \theta \). Otra identidad útil es la identidad recíproca, que relaciona las funciones trigonométricas con sus recíprocos:
\( \csc(\theta) = \frac{1}{\sin(\theta)} \)
\( \sec(\theta) = \frac{1}{\cos(\theta)} \)
\( \cot(\theta) = \frac{1}{\tan(\theta)} \)
Hay muchas otras identidades trigonométricas que se pueden usar para simplificar expresiones trigonométricas o resolver ecuaciones trigonométricas.
En general, las funciones trigonométricas de cualquier ángulo son un concepto importante en matemáticas y tienen una amplia gama de aplicaciones en campos como la física, la ingeniería y la geometría.
Fórmula de Rotación
Las fórmulas de rotación son un conjunto de ecuaciones utilizadas para calcular las nuevas coordenadas de un punto después de que ha sido rotado por un ángulo dado alrededor de un punto fijo en un sistema de coordenadas. Hay varias variaciones de estas fórmulas dependiendo del problema específico, pero explicaré la idea básica detrás de ellas.
Supongamos que tenemos un punto \(P\) en el sistema de coordenadas, con coordenadas \((x,y)\). Queremos rotar este punto alrededor de un punto fijo \(O\) (llamado el origen de la rotación) por un ángulo de \( \theta \). El objetivo es encontrar las nuevas coordenadas \((x',y' ) \) de \(P\) después de esta rotación.
Para hacer esto, usamos un conjunto de ecuaciones que relacionan las nuevas coordenadas con las coordenadas originales y el ángulo de rotación. Una forma de derivar estas ecuaciones es usando trigonometría básica. Específicamente, podemos considerar el triángulo formado por el origen de rotación \(O\), el punto original \(P\), y el punto rotado \(P'\). Los lados de
este triángulo tienen longitudes \(x\), \(y\), y \(r\) (la distancia de O a P), y el ángulo entre el eje \(x\) y la línea \(OP\) es \( \varphi \). Después de la rotación, el ángulo entre el eje \(x\) y la línea \(OP'\) es \( \varphi +\theta \).
Usando trigonometría, podemos expresar las nuevas coordenadas \((x',y' ) \) en términos de las coordenadas originales \((x,y)\) y el ángulo de rotación \(\theta \) de la siguiente manera:
\( x' = x\cos(\theta ) - y\sin( \theta ) \)
\( y' = x\sin(\theta ) + y\cos( \theta ) \)
Estas ecuaciones nos dan las nuevas coordenadas de \(P'\) después de rotar \(P\) por un ángulo \( \theta \) alrededor de \(O\).
Para entender por qué estas ecuaciones funcionan, considera la primera ecuación. El coseno de \( \theta \) representa el cambio en la coordenada \(x\) de \(P\) después de rotarlo por \( \theta \), mientras que el seno de \( \theta \) representa el cambio en la coordenada \(y\). Por lo tanto, \( x\cos( \theta ) \) representa la nueva coordenada \(x\) de \(P'\)
obtenida al rotar la coordenada \(x\) original de \(P\), y \(y\sin(\theta ) \) representa la nueva coordenada \(y\) obtenida al rotar la coordenada \(y\) original. Restando estas cantidades, obtenemos la nueva coordenada \(x\) de \(P'\) relativa al eje \(x\). De manera similar, la segunda ecuación nos da la nueva coordenada \(y\) de \(P'\) relativa al eje \(y\).
Hay varias variaciones de las fórmulas de rotación que se usan en diferentes contextos. Aquí hay algunos ejemplos:
Rotación sobre un punto que no sea el origen:
Las fórmulas básicas de rotación asumen que el punto \(P\) está siendo rotado alrededor del origen. Si queremos rotar el punto alrededor de un punto diferente \(Q\), podemos primero trasladar el sistema de coordenadas para que \(Q\) se convierta en el origen, luego aplicar las fórmulas básicas, y finalmente trasladar el sistema de coordenadas de vuelta.
Alternativamente, podemos usar una forma más general de las fórmulas de rotación que tenga en cuenta las coordenadas del punto \(Q\). Por ejemplo, si queremos rotar el punto \(P\) por un ángulo \( \theta \) sobre el punto \(Q\) con coordenadas \((a,b)\), las nuevas coordenadas \((x',y') \) se pueden calcular de la siguiente manera:
\( x' = (x-a) \cdot \cos(\theta ) - (y-b) \cdot \sin(\theta ) + a \)
\( y' = (x-a) \cdot \sin(\theta ) + (y-b) \cdot \cos(\cdot ) + b \)
Rotación de números complejos:
En análisis complejo, un número complejo \(z\) se puede representar como \(z=x+yi\), donde \(x\) e \(y\) son las partes real e imaginaria, respectivamente. Una rotación del plano complejo se puede representar como una multiplicación del número complejo \(z\) por un número complejo de la forma \(w=\cos(\theta )+i\sin(\theta ) \), donde \( \theta \) es el ángulo de
rotación. El número complejo resultante \(z'=wz\) tiene el efecto de rotar \(z\) en sentido contrario a las agujas del reloj alrededor del origen por un ángulo de \( \theta\).
En resumen, las fórmulas de rotación son una herramienta fundamental en geometría y física que nos permiten transformar puntos y objetos al rotarlos alrededor de un punto o eje fijo. Se pueden expresar en diversas formas dependiendo del problema y se utilizan en una amplia gama de aplicaciones.
Los ángulos de rotación más comunes son \( 90^\circ \), \( 180^\circ \) y \(270^\circ \).
| Tipo de Rotación | Un punto en la Imagen | Un punto en la Imagen después de la Rotación |
|---|---|---|
| \(90^\circ\) en el sentido de las agujas del reloj. | \((x,y)\) | \( (y,-x) \) |
| \( 90^\circ\) en sentido contrario a las agujas del reloj | \( (x,y) \) | \( (-y,x) \) |
| \( 180^\circ\) en el sentido de las agujas del reloj. | \( (x,y) \) | \( (-x,-y) \) |
| \( 180^\circ\) en sentido contrario a las agujas del reloj | \( (x,y) \) | \( (-x,-y) \) |
| \( 270^\circ\) en el sentido de las agujas del reloj. | \( (x,y) \) | \( (-y,x) \) |
| \( 270^\circ\) en sentido contrario a las agujas del reloj | \( (x,y) \) | \( (y,-x) \) |
Ten en cuenta que en la tabla, el punto \((x,y)\) representa las coordenadas de un punto en la imagen original antes de la rotación, y el punto en la tercera columna representa las coordenadas del mismo punto después de la rotación. El ángulo de rotación se mide en grados, y las direcciones "en el sentido de las agujas del reloj" y "en sentido contrario a las agujas del reloj" se refieren a la dirección de rotación alrededor del origen.
Identidades trigonométricas
Las identidades trigonométricas son ecuaciones matemáticas que involucran las funciones trigonométricas (seno, coseno, tangente, etc.) y son verdaderas para todos los valores posibles de las variables involucradas. Estas identidades se utilizan ampliamente en trigonometría y cálculo para simplificar y manipular expresiones que involucran funciones trigonométricas.
Aquí tienes algunas de las identidades trigonométricas más importantes:
Identidad pitagórica:
\( \sin^2 (x) + \cos^2 (x) = 1 \)
Esta identidad relaciona las funciones seno y coseno y expresa el hecho de que la suma de sus cuadrados siempre es igual a uno. Se deriva del teorema de Pitágoras en geometría, que establece que la suma de los cuadrados de las longitudes de los catetos de un triángulo rectángulo es igual al cuadrado de la longitud de la hipotenusa.
Identidades recíprocas:
\( \sin(x) = \frac{1}{\csc(x)} \)
\( \cos(x) = \frac{1}{\sec(x)} \)
\( \tan(x) = \frac{1}{\cot(x)} \)
Estas identidades expresan las relaciones recíprocas entre las funciones trigonométricas y sus funciones recíprocas correspondientes (cosecante, secante y cotangente). Por ejemplo, la primera identidad establece que el seno de un ángulo es igual al recíproco de la cosecante de ese ángulo.
Identidades de paridad:
\( \sin(-x) = -\sin(x) \)
\( \cos(-x) = \cos(x) \)
Estas identidades expresan la simetría par-impar de las funciones seno y coseno. Establecen que la función seno es una función impar (es decir, cambia de signo cuando el ángulo se nega), mientras que la función coseno es una función par (es decir, permanece igual cuando el ángulo se nega).
Identidades de suma y diferencia:
\( \sin(x+y) = \sin(x) \cos(y) + \cos(x) \sin(y) \)
\( \sin(x-y) = \sin(x) \cos(y) - \cos(x) \sin(y) \)
\( \cos(x+y) = \cos(x) \cos(y) - \sin(x)\sin(y) \)
\( \cos(x-y) = \cos(x) \cos(y) + \sin(x)\sin(y) \)
Estas identidades expresan las funciones trigonométricas de la suma y diferencia de dos ángulos en términos de las funciones trigonométricas de los ángulos individuales. Se utilizan ampliamente en cálculo y otras ramas de las matemáticas para simplificar expresiones que involucran funciones trigonométricas.
Identidades del doble ángulo:
\( \sin (2x) = 2 \sin (x) \cos (x) \)
\( \cos(2x) = \cos^2 (x) - \sin^2 (x) = \) \(2\cos^2 (x) - 1 = 1-2 \sin^2 (x) \)
Estas identidades expresan las funciones trigonométricas del doble de un ángulo en términos de las funciones trigonométricas del ángulo mismo. Se utilizan ampliamente en cálculo y otras ramas de las matemáticas para simplificar expresiones que involucran funciones trigonométricas.
Identidades del medio ángulo:
\( \sin( \frac{x}{2} ) = \pm \sqrt{ \frac{1- \cos x}{2} } \)
\( \cos( \frac{x}{2} ) = \pm \sqrt{ \frac{1+ \cos x}{2} } \)
\( \tan( \frac{x}{2} ) = \pm \sqrt{ \frac{1- \cos x}{1+ \cos x} } \)
Estas identidades expresan las funciones trigonométricas de la mitad de un ángulo en términos de las funciones trigonométricas del ángulo mismo. Se utilizan ampliamente en cálculo y otras ramas de las matemáticas para simplificar expresiones que involucran funciones trigonométricas.
Identidades de producto a suma:
\( \sin(x)\sin(y) = \frac{1}{2} [\cos(x-y) - \cos(x+y) ] \)
\( \cos(x) \cos(y) = \frac{1}{2} [\cos(x-y) + \cos(x+y) ] \)
\( \sin(x) \cos(y) = \frac{1}{2} [\sin(x+y) + \sin(x-y) ] \)
Estas identidades expresan el producto de dos funciones trigonométricas como una suma o diferencia de funciones trigonométricas. Se utilizan para simplificar productos que involucran funciones trigonométricas.
Identidades de suma a producto:
\( \sin(x) + \sin(y) = 2 \sin [ \frac{x+y}{2} ] \cos [ \frac{x-y}{2} ] \)
\( \sin (x) - \sin (y) = 2 \cos [ \frac{x+y}{2} ] \sin [ \frac{x-y}{2} ] \)
\( \cos(x) + \cos(y) = 2 \cos[ \frac{x+y}{2} ] \cos[ \frac{x-y}{2} ] \)
\( \cos(x)-\cos(y) = -2 \sin[ \frac{x+y}{2} ] \sin[ \frac{x-y}{2} ] \)
Estas identidades expresan la suma o diferencia de dos funciones trigonométricas como un producto de funciones trigonométricas. Se utilizan para simplificar sumas o diferencias que involucran funciones trigonométricas.
Identidades de cofunción:
\( \sin(x) = \cos( 90^\circ - x) \)
\( \cos(x) = \sin( 90^\circ - x) \)
\( \tan(x) = \cot( 90^\circ - x) \)
\( \cot(x) = \tan( 90^\circ - x) \)
Estas identidades expresan la relación entre una función trigonométrica y su cofunción (es decir, la función del ángulo complementario). Se utilizan para simplificar expresiones que involucran ángulos complementarios.
Identidades de periodicidad:
\( \sin(x + 2 \pi) = \sin(x) \)
\( \cos(x + 2 \pi ) = \cos(x) \)
\( \tan(x + \pi ) = \tan(x) \)
Estas identidades expresan la naturaleza periódica de las funciones trigonométricas. Establecen que las funciones seno y coseno se repiten cada \(2 \pi \) radianes, mientras que la función tangente se repite cada \( \pi \) radianes.
Estas son algunas de las identidades trigonométricas más importantes que se utilizan en matemáticas. Al memorizar estas identidades y entender cómo aplicarlas, los estudiantes pueden volverse competentes en trigonometría y resolver problemas desafiantes que involucran funciones trigonométricas.
Simplificación de expresiones trigonométricas
Las funciones trigonométricas son una parte esencial de las matemáticas y la física, y simplificar expresiones trigonométricas es una habilidad importante para resolver ecuaciones y demostrar identidades. Simplificar expresiones trigonométricas implica manipularlas algebraicamente hasta que estén en una forma más simple que sea más fácil de trabajar.
Las funciones trigonométricas más comunes son el seno (sin), coseno (cos), tangente (tan), cotangente (cot), secante (sec), y cosecante (csc). Estas funciones pueden definirse en términos de las razones de los lados de un triángulo rectángulo, o como funciones en el círculo unitario.
Para simplificar una expresión trigonométrica, es necesario utilizar varias identidades y propiedades trigonométricas. Algunas de las identidades más comúnmente utilizadas son:
Identidades pitagóricas:
\( \sin^2(\theta) + \cos^2(\theta) = 1 \)
\( \tan^2(\theta) + 1 = \sec^2(\theta) \)
\( 1 + \cot^2(\theta) = \csc^2(\theta) \)
Identidades de suma y diferencia de ángulos:
\( \sin(\alpha \pm \beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta) \)
\( \cos(\alpha \pm \beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta) \)
\( \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)} \)
Identidades del doble ángulo:
\( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \)
\( \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) \)
\( \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \)
Identidades del medio ángulo:
\( \sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}} \)
\( \cos\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 + \cos(\theta)}{2}} \)
\( \tan\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}} \)
Usando estas identidades, se puede simplificar una expresión trigonométrica paso a paso hasta que esté en su forma más simple. Algunos ejemplos de simplificación de expresiones trigonométricas son:
\( \sin^2 (x)+\cos^2 (x) \rightarrow 1 \)
\( \frac{\sin^2 (x)}{1-\cos(x)} \rightarrow \frac{1+\cos(x)}{2-\cos(x)} \)
\( \frac{\sin(x)}{\cos(x)} - \frac{\cos(x)}{\sin(x)} \rightarrow \frac{\sin^2 (x)-\cos^2 (x)}{\sin(x)\cos(x)} \)
\( \frac{\sin(x)}{\cos(x) +1} + \frac{1}{\cos(x)-1} \rightarrow \frac{2\sin(x)}{\cos^2 (x)-1} \)
Es importante tener en cuenta que al simplificar expresiones trigonométricas, se debe prestar atención al dominio de la expresión. Algunas funciones trigonométricas no están definidas para ciertos valores del ángulo, como \( \tan(\theta) \) y \( \cot(\theta) \) para \( \theta = \frac{\pi}{2} +k \pi \) donde \(k\) es un entero. Además, algunas identidades solo son
válidas para ciertos valores del ángulo o cuando se cumplen ciertas condiciones, como las identidades del medio ángulo que solo son válidas para \( \frac{\pi}{2} \le \theta \le \pi \) y \( \cos(\theta) \le 0 \).
En resumen, la simplificación de expresiones trigonométricas implica utilizar varias identidades y propiedades para manipularlas algebraicamente hasta que estén en una forma más simple. Se debe prestar atención al dominio de la expresión y asegurarse de que las identidades utilizadas sean válidas para los valores dados del ángulo.