Funciones periódicas. Periodicidad de las funciones trigonométricas. ☰

Las funciones periódicas son aquellas que repiten sus valores en intervalos regulares o períodos. El concepto de periodicidad es importante en varias ramas de las matemáticas, como el análisis de Fourier y el procesamiento de señales. Una función \(f(x)\) se dice que es periódica si existe una constante no nula \(P\) tal que para todo \(x\) en el dominio de \(f\), se cumple la siguiente condición:
\(f(x+P)=f(x)\).

El valor más pequeño y positivo de \(P\) para el cual se cumple esta condición se llama el periodo de la función.

Las funciones trigonométricas, como el seno y el coseno, son ejemplos fundamentales de funciones periódicas. Veamos la periodicidad de las funciones seno y coseno:

Función seno: La función seno, denotada por \( \sin(x) \), es periódica con un período de \( 2 \pi \). Esto significa que para todo \(x\):
\( \sin(x+2 \pi )=\sin(x) \).

En otras palabras, la función seno repite sus valores cada \( 2 \pi \) unidades a lo largo del eje \(x\).

Función coseno: La función coseno, denotada por \( \cos(x) \), también es periódica con un período de \( 2 \pi \). Esto significa que para todo \(x\):
\( \cos(x+ 2 \pi )=\cos(x) \).

Al igual que la función seno, la función coseno también repite sus valores cada \( 2 \pi \) unidades a lo largo del eje \(x\).

La función tangente, denotada por \( \tan(x) \), es otro ejemplo de una función trigonométrica periódica. Sin embargo, su período es diferente al de las funciones seno y coseno. La función tangente tiene un período de \( \pi \), lo que significa que para todo \(x\):
\( \tan(x+ \pi )=\tan(x) \).

La función tangente repite sus valores cada \( \pi \) unidades a lo largo del eje \(x\).

En resumen, las funciones trigonométricas son funciones periódicas, con las funciones seno y coseno teniendo un período de \( 2 \pi \), y la función tangente teniendo un período de \( \pi \). Estas propiedades periódicas son esenciales para resolver ecuaciones trigonométricas y analizar fenómenos periódicos en diversas aplicaciones científicas y de ingeniería.

Gráficos de las funciones seno (y=sin(x)) y coseno (y=cos(x)) ☰

Los gráficos de las funciones seno y coseno, \( y=sin(x) \) y \(y=cos(x) \), son esenciales para comprender sus propiedades y comportamiento. Ambas funciones son periódicas y oscilan entre \(-1\) y \(1\). Los gráficos exhiben la periodicidad y la amplitud de estas funciones. Veamos en detalle los gráficos de ambas funciones.

Gráfico de \( y=sin(x) \):
La función seno tiene un período de \( 2 \pi \). Esto significa que repite sus valores cada \( 2 \pi \) unidades a lo largo del eje \(x\). El gráfico de la función seno comienza en el origen \((0,0)\) y oscila entre \(-1\) y \(1\) con algunos puntos clave:
\( x = \frac{ \pi }{2} \), \( sin(x)=1 \) (valor máximo)
\( x = \pi \), \( sin(x) = 0 \) (cruce por cero)
\( x= \frac{3 \pi }{2} \), \( sin(x)= -1 \) (valor mínimo)
\(x=2 \pi \), \( sin(x)=0 \) (cruce por cero y un ciclo completo)

La función seno tiene una forma de onda y su gráfico es simétrico respecto al origen (función impar). El gráfico se extiende infinitamente en ambas direcciones positiva y negativa de \(x\), repitiendo su patrón cada \(2 \pi \) unidades.


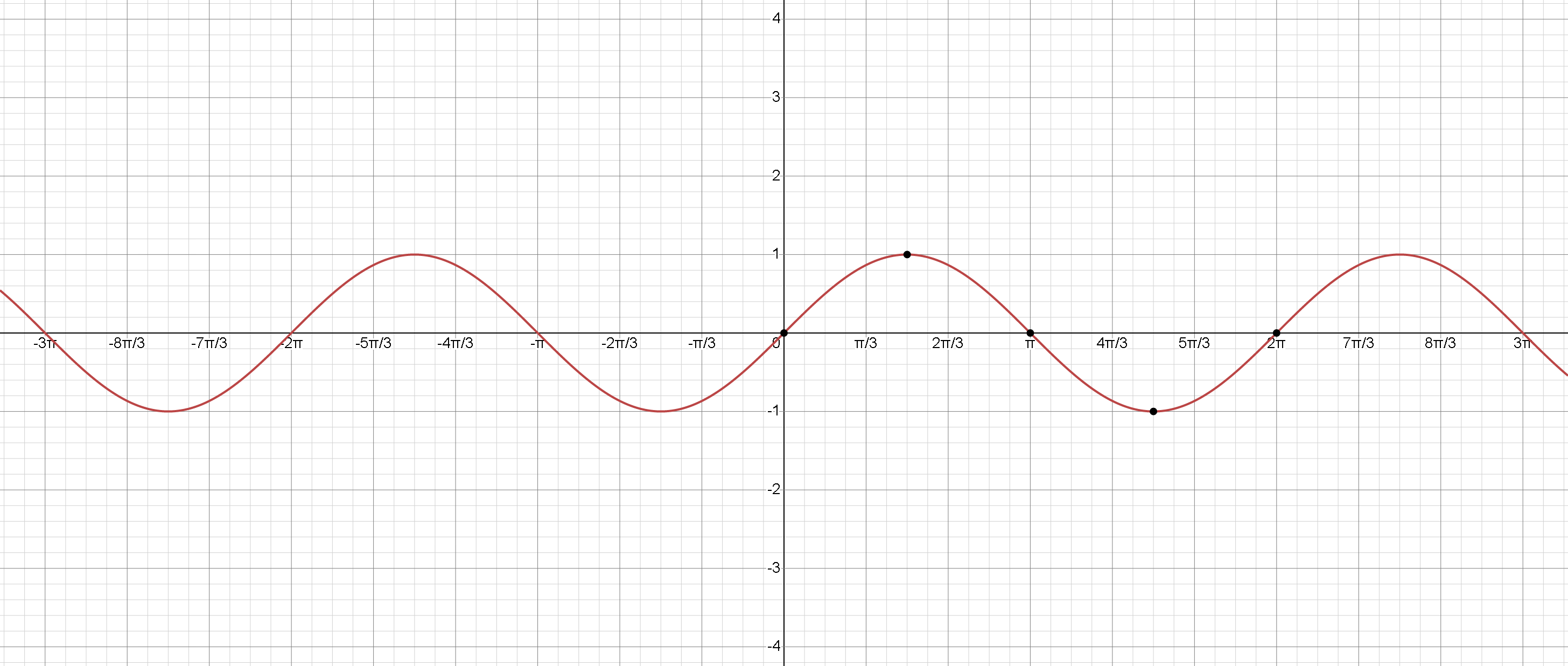
Gráfico de \(y=cos(x) \):
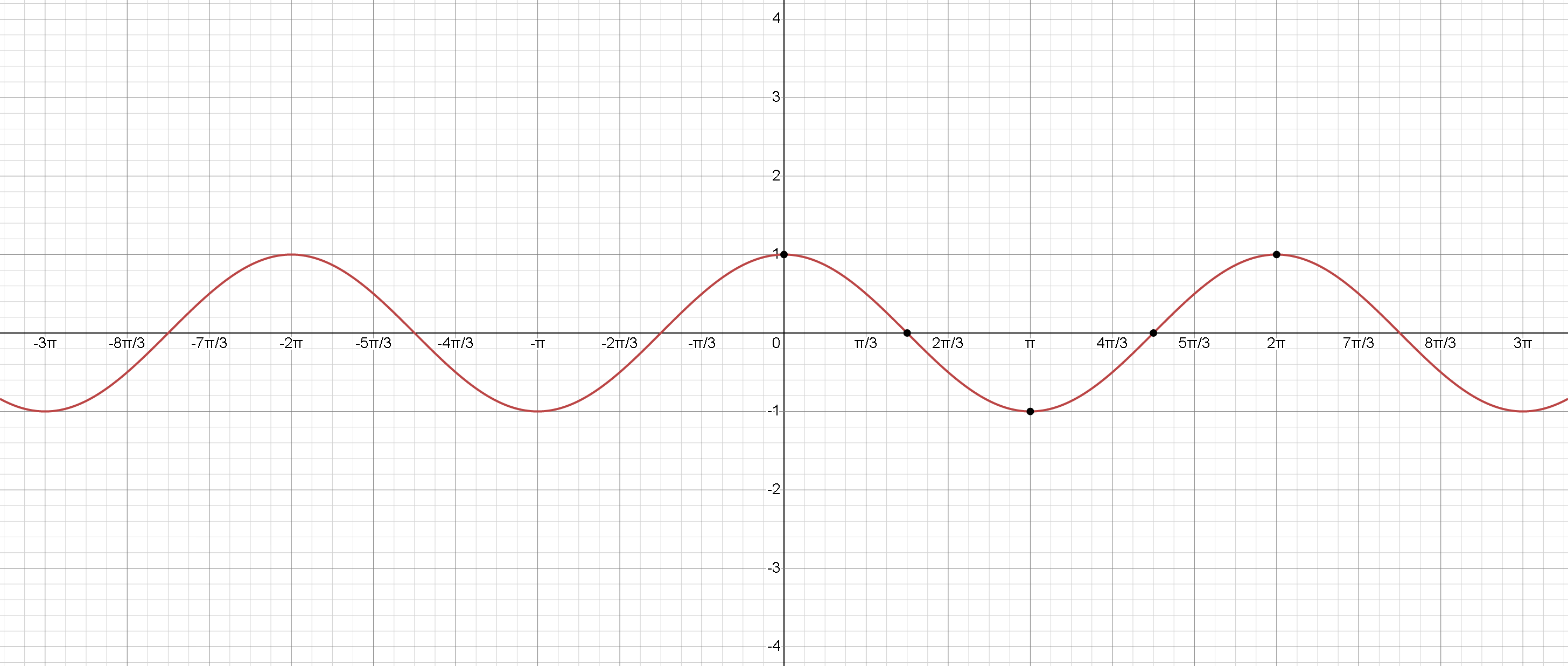
La función coseno, al igual que la función seno, tiene un período de \(2 \pi \) y oscila entre \(-1\) y \(1\). Sin embargo, el gráfico de la función coseno está desplazado \( \frac{\pi}{2} \) unidades a la izquierda en comparación con la función seno. Aquí hay algunos puntos clave para la función coseno:
\( x =0 \), \( cos(x)=1 \) (valor máximo)
\( x = \frac{ \pi }{2} \), \( cos(x)=0 \) (cruce por cero)
\( x = \pi \), \( cos(x)= -1 \) (valor mínimo)
\( x= \frac{3 \pi }{2} \), \( cos(x)=0 \) (cruce por cero)
\(x = 2 \pi \), \( cos(x)= 1\) (cruce por cero y un ciclo completo)

La función coseno también tiene una forma de onda y su gráfico es simétrico respecto al eje \(y\) (función par). El gráfico se extiende infinitamente en ambas direcciones positiva y negativa de \(x\), repitiendo su patrón cada \( 2 \pi \) unidades.

En resumen, los gráficos de las funciones seno y coseno son patrones periódicos en forma de onda que oscilan entre \(-1\) y \(1\). Tienen un período de \( 2 \pi \), con la función coseno desplazada \( \frac{\pi }{2} \) unidades a la izquierda en comparación con la función seno. Estos gráficos ayudan a visualizar las propiedades y el comportamiento de las funciones seno y coseno, que son fundamentales en la trigonometría y diversas aplicaciones en matemáticas, ciencias e ingeniería.

Transformaciones de las funciones seno y coseno☰

Las transformaciones de las funciones seno y coseno implican modificar las funciones seno y coseno básicas para crear nuevas funciones con diferentes propiedades, como amplitud, período, desplazamiento de fase y desplazamiento vertical. Estas transformaciones nos permiten modelar una amplia gama de fenómenos periódicos en diversos campos, como la física, la ingeniería y la música. Las funciones seno y coseno básicas están dadas por:
\( f(x) = sin(x) \)
\( g(x) = cos(x) \)

Aquí hay un breve resumen de las cuatro transformaciones comunes:

Amplitud: La amplitud es el valor pico de la función, o la distancia máxima desde el eje central de la función. Cambiar la amplitud implica multiplicar la función seno o coseno por una constante, denotada por "\(A\)":
\( f(x)= Asin(x) \)
\( g(x) = Acos(x) \)

Si \( A > 1 \), la amplitud aumenta, y si \( 0 < A < 1 \) , la amplitud disminuye. Si \(A\) es negativo, la función se refleja sobre el eje horizontal.

Período: El período es el intervalo sobre el cual la función se repite. Para cambiar el período de la función seno o coseno, multiplicamos la variable de entrada \((x)\) por una constante, denotada por "\(B\)":
\( f(x) = sin(Bx) \)
\( g(x) = cos(Bx) \)

El nuevo período de la función se encuentra dividiendo el período original (\( 2 \pi \) tanto para las funciones seno como para las funciones coseno) por el valor absoluto de \(B\):
\( \text{Nuevo período } = \frac{2 \pi }{ |B| } \). Si \( B > 1 \) , la función se comprime horizontalmente, y si \( 0 < B < 1 \) , la función se estira horizontalmente.

Desplazamiento de fase: El desplazamiento de fase es un desplazamiento horizontal de la función. Se logra sumando o restando una constante, denotada por "\(C\)", de la variable de entrada \((x)\):
\( f(x) = sin( B \cdot (x-C) ) \)
\( g(x) = cos ( B \cdot (x-C) ) \)

Un desplazamiento de fase positivo \( (C > 0 ) \) mueve la función hacia la derecha, y un desplazamiento de fase negativo \( (C < 0) \) mueve la función hacia la izquierda.

Desplazamiento vertical: El desplazamiento vertical mueve la función hacia arriba o hacia abajo al agregar o restar una constante, denotada por "\(D\)", a toda la función:
\( f(x) = Asin(B(x - C)) + D \)
\( g(x) = Acos(B(x - C)) + D \)

Un desplazamiento vertical positivo \((D > 0) \) mueve la función hacia arriba, y un desplazamiento vertical negativo \( (D < 0) \) mueve la función hacia abajo.

En resumen, las transformaciones de las funciones seno y coseno implican alterar su amplitud, período, desplazamiento de fase y desplazamiento vertical para modelar diversos fenómenos periódicos. Las funciones seno y coseno transformadas generalmente se pueden escribir como:
\( f(x) = Asin(B(x-C))+D \)
\( g(x) = Acos(B(x-C))+D \)

Para seguir explorando las transformaciones de las funciones seno y coseno, veamos algunos ejemplos y aplicaciones de estas transformaciones.

Ejemplo 1: Procesamiento de señales
En el procesamiento de señales, la modulación de amplitud \((AM)\) es una técnica utilizada para transmitir información variando la amplitud de una señal de onda continua. La modulación se puede representar por el producto de la onda portadora y la señal de mensaje:
\( y(t)= (A + Msin(Bmt)) \cdot cos(Bc\cdot t) \)

Aquí, \(A\) representa la amplitud de la onda portadora, \(Bc\) es la frecuencia angular de la onda portadora, \(M\) es la amplitud de la señal de mensaje, \(Bm\) es la frecuencia angular de la señal de mensaje, y \(t\) es la variable de tiempo. La transformación permite la combinación de una onda portadora de alta frecuencia con una señal de mensaje de baja frecuencia.

Ejemplo 2: Física - Movimiento armónico simple
En física, el movimiento armónico simple \((SHM)\) describe el movimiento de un objeto oscilante, como una masa unida a un resorte o un péndulo. El desplazamiento del objeto desde su posición de equilibrio en función del tiempo se puede modelar utilizando una función seno o coseno:
\( x(t) = A\cos(\omega t + \varphi) \)

Aquí, \(A\) es la amplitud del movimiento, \( \omega \) es la frecuencia angular, \(t\) es el tiempo, y \( \varphi \) es el ángulo de fase. El ángulo de fase determina la posición inicial del objeto en \(t = 0\). El movimiento armónico simple se puede analizar y predecir utilizando funciones seno y coseno transformadas.

Ejemplo 3: Sonido y Música
En acústica, las ondas sonoras se pueden modelar utilizando funciones seno y coseno. La forma de onda de un tono puro se puede representar como:
\( y(t) = Asin(2 \pi f \cdot t + \varphi ) \)

Aquí, \(A\) es la amplitud de la onda de sonido, que determina la intensidad; \(f\) es la frecuencia de la onda de sonido, que determina el tono; \(t\) es la variable de tiempo, y \( \varphi \) es el ángulo de fase, que determina la posición inicial de la onda. Al transformar funciones seno y coseno, podemos analizar y sintetizar sonidos y música complejos.

Estos ejemplos ilustran la versatilidad de las funciones seno y coseno transformadas en diversos campos. Al ajustar la amplitud, el período, el desplazamiento de fase y el desplazamiento vertical, podemos modelar una amplia gama de fenómenos periódicos y resolver problemas en diversas disciplinas.

Gráficos de las funciones tangente y cotangente ☰

La tangente y la cotangente son funciones trigonométricas que están relacionadas con las funciones seno y coseno. Son periódicas y exhiben propiedades únicas que las hacen interesantes de estudiar. Aquí tienes una mirada detallada a los gráficos de estas dos funciones:

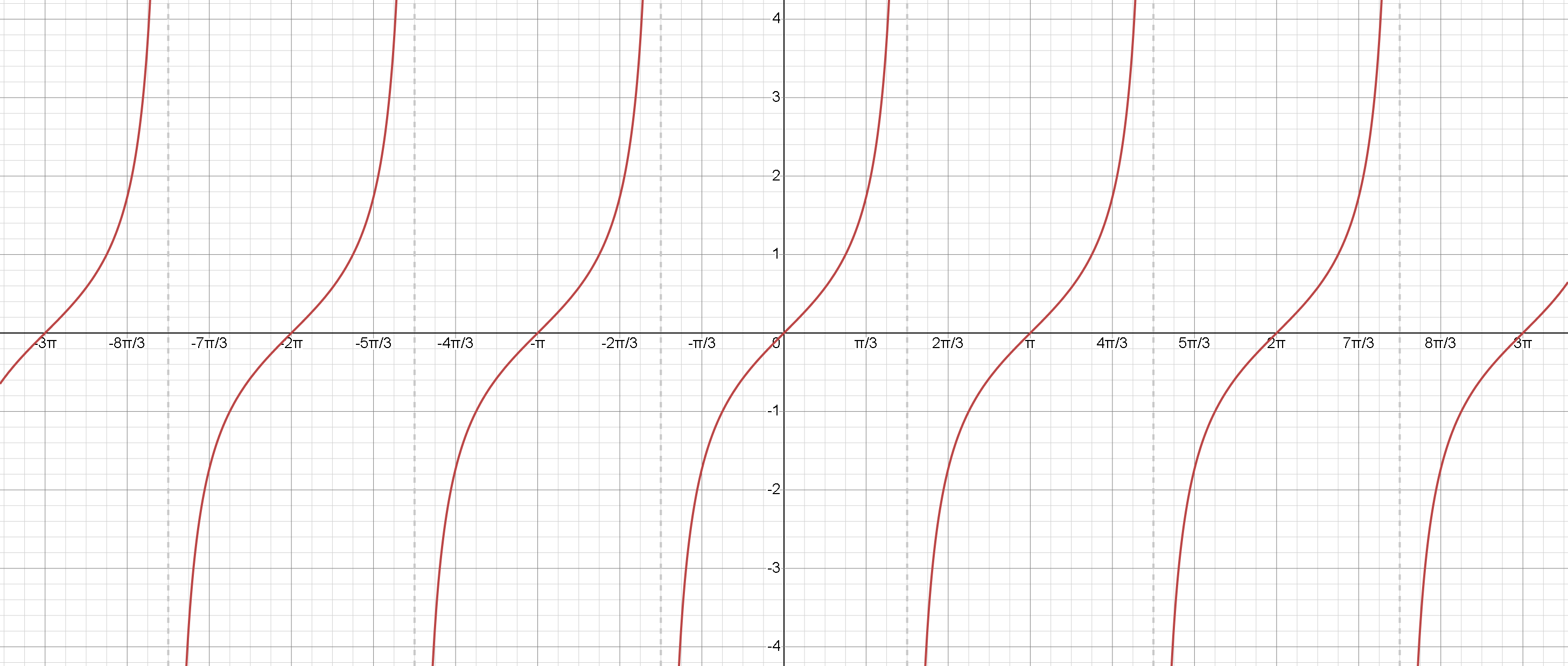
1. Función Tangente \( \tan(x) \):
La función tangente se define como la razón entre la función seno y la función coseno, es decir.
\( \tan(x) = \frac{sin(x)}{cos(x)} \)

Características clave del gráfico de la tangente:

• Período: La función tangente tiene un período de \( \pi \), lo que significa que se repite cada \( \pi \) unidades a lo largo del eje \(x\).
• Asíntotas: Dado que la función tangente es la razón de seno y coseno, es indefinida cuando la función coseno es cero. Esto ocurre en múltiplos impares de \( \frac{ \pi }{2} \). ( \( \pm \frac{ \pi }{2} \), \( \pm \frac{ 3 \pi }{2} \), etc.).
  Estos puntos son donde ocurren las asíntotas verticales.
• Rango: El rango de la función tangente es (\( - \infty ; \infty ) \), ya que la función toma todos los valores reales.
• Simetría: La función tangente es una función impar, lo que significa que es simétrica respecto al origen.
  En otras palabras, \( tg(-x) = -tg(x) \)
• Incremento: La función tangente siempre está aumentando en cada uno de sus períodos.

2. Función Cotangente \( \cot(x) \):
La función cotangente se define como la razón de la función coseno y la función seno, es decir.
\( \cot(x) = \frac{cos(x)}{sin(x)} \)

Características clave del gráfico de la cotangente:

• Período: La función cotangente tiene un período de \( \pi \), lo que significa que se repite cada \( \pi \) unidades a lo largo del eje \(x\), al igual que la función tangente.
• Asíntotas: Dado que la función cotangente es la razón de coseno y seno, es indefinida cuando la función seno es cero. Esto ocurre en múltiplos enteros de \(\pi\). (0, \( \pm \pi\), \( \pm 2 \pi \), etc). Estos puntos son donde ocurren las asíntotas verticales.
• Rango: El rango de la función cotangente es \( (- \infty, \infty ) \), ya que la función toma todos los valores reales.
• Simetría: La función cotangente es una función impar, lo que significa que es simétrica respecto al origen.
  En otras palabras, \(cot(-x)=-cot(x)\).
• Decremento: La función cotangente siempre está disminuyendo en cada uno de sus períodos.

En resumen, tanto la función tangente como la función cotangente son periódicas, con un período de \( \pi \), y exhiben simetría impar. Tienen asíntotas verticales y comportamientos diferentes, con la función tangente siendo creciente mientras que la función cotangente es decreciente.

Funciones trigonométricas inversas ☰

Las funciones trigonométricas inversas, también conocidas como arcoseno, arcocoseno y arcotangente, son las funciones inversas de las funciones trigonométricas básicas: seno, coseno y tangente. Estas funciones te permiten encontrar el ángulo cuando conoces el valor trigonométrico. Hay seis funciones trigonométricas inversas principales:

1. Seno inverso. \( \sin^{-1} (x) \) o \( \arcsin(x) \):
La inversa de la función seno.
Dominio: \( [-1 , 1 ] \)
Rango: \( [- \frac{ \pi }{2}, \frac{ \pi }{2} ] \)

2. Coseno inverso. \( \cos^{-1} (x) \) o \( \arccos(x) \):
La inversa de la función coseno.
Dominio: \( [-1 , 1 ] \)
Rango: \( [ 0 , \pi ] \)

3. Tangente inversa. \( \tan^{-1} (x) \) o \( \arctan(x) \):
La inversa de la función tangente.
Dominio: ( \(- \infty , \infty \) )
Rango: ( \( - \frac{ \pi }{2}, \frac{ \pi }{2} \) )

4. Cosecante inversa. \( \csc^{-1} (x) \) o \( \arccsc(x) \):
La inversa de la función cosecante (que es el recíproco de la función seno).
Dominio: \( (-\infty, -1] \cup [1, \infty) \)
Rango: \( \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right]\)

5. Secante inversa. \( \sec^{-1} (x) \) o \( \arcsec(x) \):
La inversa de la función secante (que es el recíproco de la función coseno).
Dominio: \( \left(-\infty, -1\right] \cup \left[1, \infty\right) \)
Rango: \( \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] \)

6. Cotangente inversa. \( \cot^{-1} (x) \) o \( \arccot(x) \):
La inversa de la función cotangente.
Dominio: ( \(- \infty , \infty \) )
Rango: ( \( 0 , \pi \) )


Propiedades de las funciones trigonométricas inversas:

⠐ Dominios y rangos restringidos: Para hacer que las funciones trigonométricas sean invertibles, sus dominios se restringen, lo que resulta en rangos restringidos para las funciones trigonométricas inversas.

⠐ Notación: Las funciones trigonométricas inversas a menudo se denotan con un prefijo "\( ^{-1} \)" o "\( arc \)". Por ejemplo, \( \sin^{-1} (x) \) o \( \arcsin(x) \) representan la función seno inversa.
Ten en cuenta que \( \sin^{-1} (x) \) NO es lo mismo que \( \frac{1}{\sin(x)} \) , que es la función recíproca (cosecante).

⠐ Composición:
La composición de una función trigonométrica y su función inversa resulta en la función identidad, siempre que la entrada esté dentro del rango correcto:

\( \sin( \arcsin(x) ) = x \), Si \(x\) está en el dominio de \( \arcsin( [-1,1] ) \)

\( \arcsin ( \sin(x) ) = x \), Si \(x\) está en el rango de \( \arcsin( [ -\frac{ \pi }{2} , \frac{ \pi }{2} ] ) \)

Relaciones similares se mantienen para las otras funciones trigonométricas inversas.

⠐ Diferenciabilidad:
Las funciones trigonométricas inversas son diferenciables dentro de sus dominios, excepto en los puntos donde las funciones trigonométricas originales tienen tangentes verticales.
Por ejemplo, las funciones arcoseno y arcocoseno no son diferenciables en \(x=-1\) y \(x=1\), y la función arcotangente no es diferenciable en \(x=- \infty \) y \(x= \infty \).

⠐ Simetría:
Algunas funciones trigonométricas inversas exhiben simetría.
Por ejemplo:
\( \arctan(-x) = -\arctan(x) \): La función tangente inversa es una función impar.

\( \arccot(-x) = \pi - \text{arcctg}(x) \): La función cotangente inversa exhibe un tipo específico de simetría.

Las funciones trigonométricas inversas son cruciales para resolver problemas que involucran triángulos y trigonometría, especialmente cuando necesitas encontrar un ángulo dado las longitudes de los lados u otros valores trigonométricos. Se utilizan en diversos campos de las matemáticas, la física y la ingeniería, como en el cálculo, la geometría y el estudio de fenómenos periódicos.

⠐ Derivadas:
Las derivadas de las funciones trigonométricas inversas son esenciales en el cálculo, particularmente al resolver problemas de integración que involucran funciones trigonométricas. Aquí están las derivadas de las tres principales funciones trigonométricas inversas:

\( \frac{d (\arcsin(x))}{dx} = \frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arccos(x))}{dx} = -\frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arctan(x))}{dx} = \frac{1}{1 + x^2} \)