Vecteurs ☰

Les vecteurs sont des objets mathématiques couramment utilisés dans divers domaines de la science, de l'ingénierie et des mathématiques. Ils sont utilisés pour représenter des grandeurs physiques telles que la force, la vitesse, l'accélération et le déplacement qui ont à la fois une magnitude et une direction.
Un vecteur est généralement représenté par une flèche avec une longueur et une direction. La longueur de la flèche représente la magnitude du vecteur, tandis que la direction de la flèche représente la direction du vecteur. La magnitude d'un vecteur est une valeur scalaire et est notée par \( \vec{|v|} \).
Les vecteurs peuvent être notés en nommant leurs points de départ et d'arrivée, où le point de départ est la queue du vecteur et le point d'arrivée est la tête du vecteur. Par exemple, le vecteur du point \(A\) au point \(B\) peut être noté \( \overrightarrow{AB} \) .

Les vecteurs possèdent un certain nombre de propriétés importantes en mathématiques et en physique. Certaines des principales propriétés des vecteurs incluent:

Magnitude: Les vecteurs ont une magnitude ou une longueur, qui est un scalaire non négatif qui représente la taille du vecteur.

Direction: Les vecteurs ont une direction, qui peut être spécifiée en utilisant des angles ou d'autres notations directionnelles. La direction d'un vecteur est définie par l'angle entre le vecteur et une direction de référence fixe.

Addition: Les vecteurs peuvent être additionnés en utilisant la loi du parallélogramme ou la loi du triangle pour l'addition vectorielle. Cela implique d'ajouter les composantes correspondantes de chaque vecteur pour obtenir le vecteur résultant.

Multiplication scalaire: Les vecteurs peuvent être multipliés par des scalaires, ce qui modifie la magnitude et/ou la direction du vecteur. La multiplication scalaire implique de multiplier chaque composante du vecteur par un scalaire.

Produit scalaire: Les vecteurs peuvent être multipliés ensemble en utilisant le produit scalaire. Le produit scalaire de deux vecteurs est un scalaire qui représente le produit de leurs magnitudes et le cosinus de l'angle entre eux.

Produit vectoriel: Les vecteurs peuvent également être multipliés en utilisant le produit vectoriel. Le produit vectoriel de deux vecteurs est un vecteur qui est perpendiculaire aux deux vecteurs d'entrée et dont la magnitude est égale au produit de leurs magnitudes fois le sinus de l'angle entre eux.

Zéro vectoriel: Il existe un vecteur unique appelé vecteur zéro, noté \( \vec{0} \), qui a une magnitude de \(0\) et aucune direction. On peut le considérer comme le vecteur qui va d'un point à lui-même, ou de manière équivalente, comme la différence entre deux vecteurs égaux.
Par exemple, \( \overrightarrow{OA} - \overrightarrow{OA} = 0 \).

Vecteur unitaire: Un vecteur unitaire est un vecteur avec une magnitude de 1. Tout vecteur non nul peut être divisé par sa magnitude pour obtenir un vecteur unitaire dans la même direction.

Vecteurs colinéaires: Les vecteurs sont colinéaires s'ils se trouvent sur la même ligne ou sont parallèles. En d'autres termes, ils ont la même ou la direction opposée. Les vecteurs colinéaires peuvent être écrits comme des multiples scalaires les uns des autres. Si deux vecteurs \( \vec{v} \) et \( \vec{w} \) sont colinéaires, alors il existe un scalaire \(k\) tel que \( \vec{v} = k \vec{w} \) ou \( \vec{w} = k \vec{v} \). Cela signifie qu'un vecteur est un multiple scalaire de l'autre, et ils pointent dans la même direction ou dans des directions opposées.

Vecteurs orthogonaux: Deux vecteurs sont orthogonaux si leur produit scalaire est nul. Les vecteurs orthogonaux sont également appelés vecteurs perpendiculaires, et ils forment un angle de 90 degrés entre eux.

Vecteurs de base: Un ensemble de vecteurs de base est un ensemble de vecteurs linéairement indépendants qui peuvent être utilisés pour représenter n'importe quel autre vecteur dans un espace. Les vecteurs de base les plus courants sont les vecteurs unitaires standard dans l'espace tridimensionnel, qui sont notés par \(\hat{i}\), \( \hat{j} \) et \( \hat{k} \).

Indépendance linéaire: Un ensemble de vecteurs est linéairement indépendant si aucun des vecteurs de l'ensemble ne peut être exprimé comme une combinaison linéaire des autres. Si un ensemble de vecteurs est linéairement indépendant, alors il peut être utilisé comme base pour un espace vectoriel.

Enveloppe: L'enveloppe d'un ensemble de vecteurs est l'ensemble de toutes les combinaisons linéaires de ces vecteurs. L'enveloppe d'un ensemble de vecteurs est un sous-espace de l'espace vectoriel contenant ces vecteurs.

Projection: La projection d'un vecteur sur un autre est la composante du premier vecteur qui se trouve dans la direction du deuxième vecteur. La projection du vecteur \( \vec{u} \) sur le vecteur \( \vec{v} \) est donnée par $$ \text{proj}_{ \vec{v}} ( \vec{u} ) = \frac{\vec{u} \cdot \vec{v}}{||\vec{v}||^2} \vec{v} $$

Composante: La composante d'un vecteur le long d'un autre est la partie du premier vecteur qui se trouve dans la direction du deuxième vecteur. La composante du vecteur \( \vec{u} \) le long du vecteur \( \vec{v} \) est donnée par \( \text{comp}_{\vec{v}} (\vec{u}) = \frac{\vec{u} \cdot v}{||\vec{v}||^2} cos \theta \), où \( \theta \) est l'angle entre \( \vec{u} \) et \( \vec{v} \).

Transport parallèle: Le transport parallèle est une manière de déplacer des vecteurs le long d'une courbe de manière à préserver leur direction. Le transport parallèle est utilisé en géométrie différentielle et dans d'autres domaines pour étudier la courbure des courbes et des surfaces.

Covariance et contravariance: En mathématiques et en physique, les vecteurs sont souvent classifiés comme covariants ou contravariants en fonction de la manière dont leurs composantes se transforment sous les transformations de coordonnées. Les vecteurs covariants ont des composantes qui se transforment de la même manière que les coordonnées, tandis que les vecteurs contravariants ont des composantes qui se transforment de manière opposée. Le concept de covariance et contravariance est largement utilisé en calcul tensoriel et dans d'autres domaines des mathématiques et de la physique.

Ce ne sont là que quelques-unes des nombreuses propriétés des vecteurs.

La longueur d'un vecteur (Magnitude) ☰

En mathématiques, la longueur d'un vecteur est également appelée sa magnitude ou sa norme. Elle représente la distance entre l'origine et l'extrémité du vecteur dans un espace géométrique.
Pour un vecteur avec des composantes \( (x, y, z) \) dans un espace tridimensionnel, sa longueur peut être calculée en utilisant la formule suivante:
\( |\vec{v}| = \sqrt{(x^2+ y^2+ z^2 )} \).

Dans un espace bidimensionnel, la formule pour la longueur d'un vecteur avec des composantes \((x, y)\) est: \( |\vec{v}| = \sqrt{(x^2+ y^2 )} \).

En général, la longueur d'un vecteur peut être calculée en utilisant le théorème de Pythagore, qui affirme que le carré de la longueur du vecteur est égal à la somme des carrés de ses composantes.

La direction d'un vecteur ☰

La direction d'un vecteur peut être déterminée en calculant son angle par rapport à un axe de référence. Cet angle est souvent mesuré dans le sens antihoraire à partir de la direction positive de l'axe de référence.
Si \( \vec{v} \) est un vecteur dans l'espace bidimensionnel avec des composantes \( (v_x,v_y ) \), alors sa direction \( \theta \) est donnée par: \( \theta = \text{arctan} \left(\frac{v_y}{v_x} \right) \), où arctan est la fonction tangente inverse.

Dans l'espace tridimensionnel, un vecteur \( \vec{v} \) avec des composantes \( (v_x,v_y,v_z ) \) peut être représenté par un segment de droite dirigé de l'origine \( (0,0,0) \) au point \( (v_x,v_y,v_z ) \). Sa direction peut être décrite par deux angles: l'angle azimutal \( \varphi \), qui est l'angle mesuré dans le sens antihoraire à partir de l'axe \(x\) positif dans le plan \(xy\) et l'angle polaire \( \theta \), qui est l'angle mesuré à partir de l'axe \(z\) positif jusqu'au segment de droite.

L'angle azimutal \( \varphi \) est donné par: \( \varphi = \text{arctan} \left(\frac{v_y}{v_x} \right) \).
si \( v_x > 0 \), et \( \varphi = \text{arctan} \left(\frac{v_y}{v_x} \right) + \pi \).
si \( v_x < 0 \), l'angle polaire \( \theta \) est donné par: \( \theta=\text{arccos} \left( \frac{v_z}{|\vec{v} |} \right) \), où \( |\vec{v} | \) est la magnitude du vecteur \( \vec{v} \).

Une autre façon de décrire la direction d'un vecteur dans l'espace tridimensionnel est d'utiliser ses cosinus directeurs. Les cosinus directeurs d'un vecteur \( \vec{v} \) avec des composantes \( (v_x,v_y,v_z ) \) sont définis comme suit: \( \cos\alpha = \frac{v_x}{|\vec{v}|} \), \( \cos\beta = \frac{v_y}{|\vec{v}|} \), \( \cos\gamma = \frac{v_z}{|\vec{v}|} \), où \( \alpha \), \( \beta \) et \( \gamma \) sont les angles entre le vecteur \( \vec{v} \) et les axes positifs \(x\), \(y\) et \(z\), respectivement.

Si les cosinus directeurs d'un vecteur sont connus, sa direction peut être déterminée en utilisant les équations suivantes: $$ \small \varphi = \begin{cases} \arccos\left(\frac{\cos\beta}{\sqrt{\cos^2\alpha + \cos^2\beta}}\right) & \text{si } \cos\alpha > 0 \\ 2\pi - \arccos\left(\frac{\cos\beta}{\sqrt{\cos^2\alpha + \cos^2\beta}}\right) & \text{si } \cos\alpha < 0 \end{cases} $$
\( \theta = \text{arccos}(\cos\gamma) \) où \( \varphi \) est l'angle azimutal et \( \theta \) est l'angle polaire.

En plus de ces méthodes, la direction d'un vecteur peut également être décrite en utilisant des vecteurs unitaires. Un vecteur unitaire est un vecteur de magnitude 1 qui pointe dans la même direction que le vecteur original. Étant donné un vecteur \( \vec{v} \), son vecteur unitaire \( \hat{v} \) peut être calculé comme suit: \( \hat{v} = \frac{\vec{v} }{|\vec{v}|} \).

Une fois que le vecteur unitaire est connu, sa direction peut être décrite par les angles \( \theta \) et \( \varphi \) comme décrit ci-dessus.
Il convient de noter que la direction d'un vecteur est indépendante de sa magnitude. Par conséquent, un vecteur et un multiple scalaire de ce vecteur ont la même direction.

Addition et soustraction de vecteurs colinéaires ☰

Les vecteurs colinéaires sont des vecteurs qui se trouvent sur la même ligne. Lorsque deux vecteurs colinéaires sont ajoutés ou soustraits, le résultat est un autre vecteur colinéaire. La magnitude du résultat est la somme ou la différence des magnitudes des deux vecteurs, selon que nous les ajoutons ou les soustrayons. La direction du résultat est la même que celle des deux vecteurs car ils sont colinéaires.

Supposons que nous ayons deux vecteurs colinéaires \( \vec{a} \) et \( \vec{b} \), avec des magnitudes \( \vec{|a|} \) et \( \vec{|b|} \) respectivement. S'ils pointent dans la même direction, leur somme est donnée par: \( \vec{a} + \vec{b} = ( \vec{|a|} + \vec{|b|} ) \hat{a} \). Où \( \hat{a} \) est le vecteur unitaire dans la direction de \( \vec{a} \). S'ils pointent dans des directions opposées, leur différence est donnée par: \( \vec{a} - \vec{b} = ( \vec{|a|} - \vec{|b|} ) \hat{a} \)

Méthodes d'addition et de soustraction de vecteurs non colinéaires ☰

Les vecteurs non colinéaires sont des vecteurs qui ne se trouvent pas sur la même ligne. Lors de l'addition ou de la soustraction de vecteurs non colinéaires, nous utilisons la loi du parallélogramme ou la loi du triangle, selon la situation.

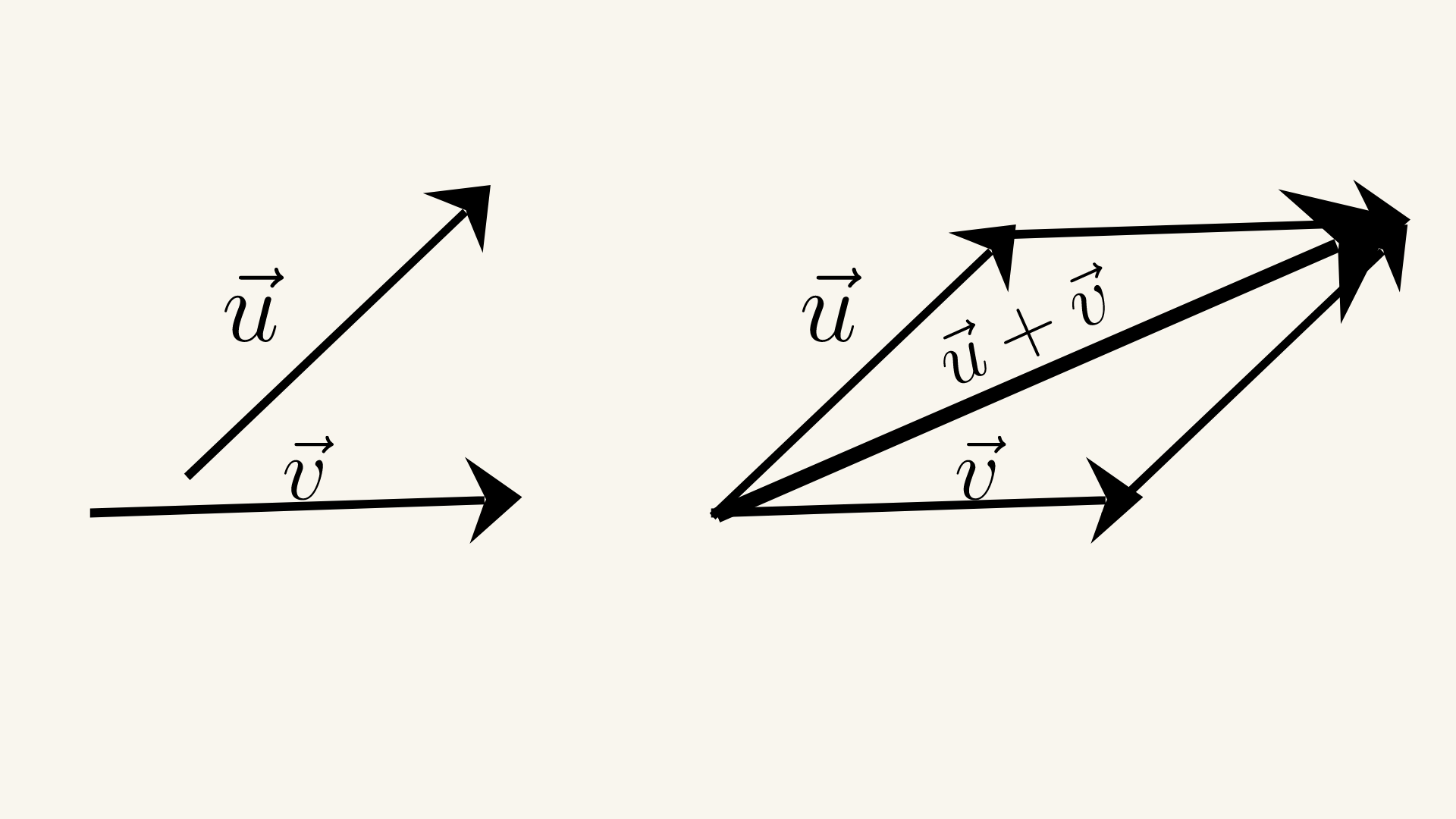
Loi du Parallélogramme
La loi du parallélogramme stipule que la somme de deux vecteurs peut être trouvée en plaçant les vecteurs tête à queue et en dessinant le parallélogramme formé par les deux vecteurs. La somme vectorielle est la diagonale du parallélogramme qui part du point commun des deux vecteurs. La loi du parallélogramme peut être utilisée pour additionner n'importe quel nombre de vecteurs, pas seulement deux. Disons que nous avons deux vecteurs non colinéaires \( \vec{a} \) et \( \vec{b} \). Nous pouvons trouver leur somme \( \vec{c} \) en utilisant la loi du parallélogramme: \( \vec{c} = a+b \).
Nous plaçons d'abord la queue du vecteur \( \vec{b} \) à la tête du vecteur \( \vec{a} \) pour former un parallélogramme. La diagonale du parallélogramme partant du point commun des deux vecteurs représente le vecteur somme \( \vec{c} \). La magnitude du vecteur somme \( \vec{c} \) peut être trouvée en utilisant la loi des cosinus: \( \vec{|c|}^2 = \vec{|a|}^2 + \vec{|b|}^2 + 2 \vec{|a|} \vec{|b|} cos \theta \), où \( \theta \) est l'angle entre les vecteurs \( \vec{a} \) et \( \vec{b} \).

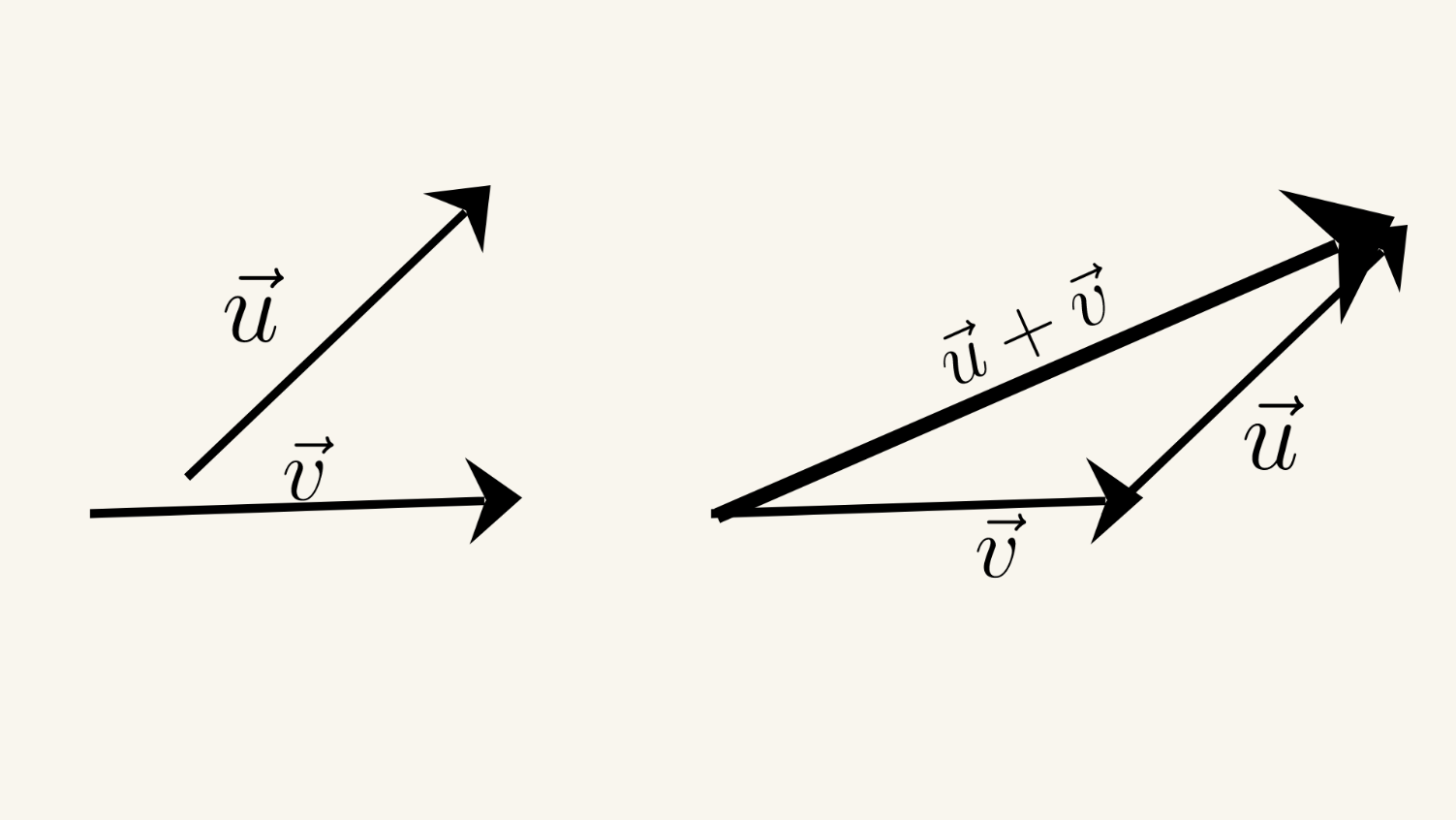
Loi du triangle
La loi du triangle stipule que la somme de deux vecteurs peut être trouvée en plaçant les vecteurs tête à queue et en dessinant le troisième côté du triangle qui relie la queue du premier vecteur à la tête du deuxième vecteur. Le vecteur somme est la diagonale du triangle qui part du point commun des deux vecteurs.
Supposons que nous ayons deux vecteurs non colinéaires \( \vec{a} \) et \( \vec{b} \). Nous pouvons trouver leur somme \( \vec{c} \) en utilisant la loi du triangle: \( \vec{c}= a+ b \).
Nous plaçons d'abord la queue du vecteur \( \vec{a} \) à l'origine puis la queue du vecteur \( \vec{b} \) à la tête du vecteur \( \vec{a} \). Le vecteur somme \( \vec{c} \) est la diagonale du triangle qui part de l'origine et relie la tête du vecteur \( \vec{b} \). La magnitude du vecteur somme \( \vec{c} \) peut être trouvée en utilisant la loi des cosinus: \( |\vec{c} |^2 = |\vec{a} |^2 + |\vec{b}|^2 -2 |\vec{a}| |\vec{b}| \cos \theta \), où \( \theta \) est l'angle entre les vecteurs \( \vec{a} \) et \( \vec{b} \).
La soustraction de vecteurs peut également être effectuée en utilisant soit la loi du parallélogramme, soit la loi du triangle. Pour soustraire le vecteur \( \vec{b} \) du vecteur \( \vec{a} \), il suffit d'inverser la direction du vecteur \( \vec{b} \) et de l'ajouter au vecteur \( \vec{a} \) en utilisant soit la loi du parallélogramme, soit la loi du triangle. \( \vec{a} - \vec{b} = \vec{a} + (-\vec{b} ) \)


Propriétés de l'addition de vecteurs
L'addition de vecteurs a plusieurs propriétés importantes qui la rendent utile en physique et dans d'autres domaines:

• Propriété commutative: L'ordre dans lequel les vecteurs sont ajoutés n'affecte pas le résultat.
  \( \vec{a} + \vec{b} = \vec{b} + \vec{a} \).
• Propriété associative: Lors de l'addition de plus de deux vecteurs, l'ordre dans lequel nous regroupons les vecteurs n'affecte pas le résultat.
  \( (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \).
• Zéro vecteur: Le vecteur zéro \( \vec{0} \), avec une magnitude nulle et n'importe quelle direction, est l'élément neutre pour l'addition des vecteurs. Ajouter le vecteur zéro à n'importe quel vecteur ne change pas le vecteur.
  \( \vec{a} + \vec{0} = \vec{a} \).
• Inverse additif: Pour chaque vecteur \( \vec{a} \), il existe un vecteur inverse additif \( -\vec{a} \) tel que leur somme soit le vecteur zéro.
  \( \vec{a} + (-\vec{a}) = \vec{0} \).
• Propriété distributive: La multiplication scalaire se distribue sur l'addition de vecteurs.
  \( (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b} \), où \(k\) est n'importe quel scalaire.

Ajout de vecteurs en utilisant les composantes ☰

Lors de l'ajout de vecteurs en utilisant les composantes, la première étape consiste à décomposer chaque vecteur en ses composantes \(x\) et \(y\). Cela peut être fait en utilisant des fonctions trigonométriques telles que le sinus et le cosinus. Par exemple, étant donné un vecteur de magnitude "\(r\)" et d'angle "\(\theta \)" par rapport à l'axe \(x\), ses composantes \(x\) et \(y\) peuvent être trouvées comme suit:
Composante \(x\): \(r\cdot \cos(\theta) \).
Composante \(y\): \(r\cdot \sin(\theta) \).

Une fois que les deux vecteurs ont été décomposés en leurs composantes \(x\) et \(y\), les composantes peuvent être additionnées séparément. Par exemple, si nous avons deux vecteurs \(A\) et \(B\), leurs composantes \(x\) peuvent être additionnées ensemble pour obtenir la composante \(x\) du vecteur résultant \(C\), et leurs composantes \(y\) peuvent être additionnées ensemble pour obtenir la composante \(y\) de \(C\):
\(C_x = A_x+ B_x \)
\(C_y= A_y+ B_y \)

Enfin, la magnitude et l'angle du vecteur \(C\) peuvent être trouvés en utilisant le théorème de Pythagore et les fonctions trigonométriques inverses, respectivement:
magnitude de \(C\): \( \sqrt{C_x^2 + C_y^2} \) .
angle de \(C\): \( \tan^{-1} \left(\frac{C_y}{C_x} \right) \) .
Notez que l'angle de C peut nécessiter un ajustement en fonction du quadrant dans lequel il se trouve, car les fonctions trigonométriques inverses donnent uniquement des angles dans la plage de \( -\frac{\pi}{2} \) à \( \frac{\pi}{2} \).

Pour ajuster l'angle du vecteur \(\vec{C} \), nous devons considérer les signes de ses composantes \(x\) et \(y\). Si \(C_x\) et \(C_y\) sont tous deux positifs, alors l'angle de \(C\) est simplement la tangente inverse de \( \frac{C_y}{C_x} \). Si \(C_x\) est négatif et \(C_y\) est positif, alors l'angle de \(C\) est de 180 degrés moins la tangente inverse de \( \frac{C_y}{|C_x|} \). Si \(C_x\) est négatif et \(C_y\) est négatif, alors l'angle de \(C\) est de 180 degrés plus la tangente inverse de \( \frac{|C_y |}{|C_x |} \). Enfin, si \(C_x\) est positif et \(C_y\) est négatif, alors l'angle de \(C\) est de 360 degrés moins la tangente inverse de \( \frac{|C_y|}{C_x} \).

Par exemple, supposons que nous ayons deux vecteurs \(A\) et \(B\) avec des magnitudes de 3 et 4, respectivement, et des angles de 30 degrés et 60 degrés par rapport à l'axe \(x\). Nous pouvons trouver les composantes \(x\) et \(y\) de chaque vecteur comme suit:
\( A_x = 3 \cdot \cos(30) = 2.598 \)
\( A_y = 3 \cdot \sin(30)= 1.5 \)
\( B_x = 4 \cdot \cos(60)= 2 \)
\( B_y = 4 \cdot \sin(60)= 3.464 \)

Nous pouvons ensuite ajouter les composantes \(x\) et \(y\) de \(A\) et \(B\) pour obtenir les composantes \(x\) et \(y\) de \(C\):
\( C_x = A_x + B_x= 4.598 \)
\( C_y = A_y + B_y= 4.964 \)

La magnitude de \(\vec{C} \) est:
\( \small \vec{|C|} = \sqrt{C_x^2+ C_y^2} = \sqrt{4.598^2 + 4.964^2} = 6.425 \)

L'angle de \(C\) est:
\( \small \theta = \tan^{-1} \left(\frac{C_y}{C_x} \right) = \tan^{-1} \left(\frac{4.964}{4.598} \right) = 49.1^\circ \)

Comme \(C_x\) et \(C_y\) sont tous deux positifs, c'est la réponse finale. Par conséquent, le vecteur résultant \(C\) a une magnitude de 6.425 et un angle de 49.1 degrés par rapport à l'axe \(x\).

Multiplication scalaire ☰

La multiplication scalaire est l'opération de multiplication d'un vecteur par un scalaire, qui est un nombre réel. Lorsqu'un vecteur est multiplié par un scalaire, la magnitude du vecteur est mise à l'échelle par la valeur absolue du scalaire, et la direction du vecteur reste inchangée si le scalaire est positif, ou est inversée si le scalaire est négatif.
Mathématiquement, la multiplication scalaire peut être exprimée comme suit: étant donné un vecteur \(v\) et un scalaire \(k\), le multiple scalaire de \( \vec{v} \) par \(k\), noté \( k \cdot \vec{v} \), est un vecteur ayant la même direction que \( \vec{v} \) mais dont la magnitude est mise à l'échelle par la valeur absolue de \(k\):
\( k \cdot \vec{v} = (|k|) \cdot \vec{v} \)

Si \(k\) est positif, alors la direction de \( k \cdot \vec{v} \) est la même que celle de \(\vec{v} \). Si \(k\) est négatif, alors la direction de \( k \cdot \vec{v} \) est opposée à celle de \( \vec{v} \).

La multiplication scalaire peut être utilisée pour étirer ou réduire des vecteurs. Par exemple, si nous avons un vecteur \( \vec{v} \) qui représente un déplacement en mètres, nous pouvons le multiplier par un scalaire pour représenter un déplacement plus grand ou plus petit que \( \vec{v} \). De plus, la multiplication scalaire peut être utilisée pour inverser la direction d'un vecteur en le multipliant par \(-1\).

La multiplication scalaire peut également être utilisée pour trouver des combinaisons linéaires de vecteurs. Une combinaison linéaire de deux vecteurs est simplement la somme des vecteurs multipliée par des coefficients scalaires.
Par exemple, étant donné deux vecteurs \( \vec{v} = (2,3) \) et \( \vec{w} = (1,-1) \), la combinaison linéaire \( 3 \vec{v} – 2 \vec{w} \) peut être calculée comme suit:
$$ \begin{align*} &3\vec{v} = 3(2,3) = (6,9)& \\ &2\vec{w} = 2(1,-1) = (2,-2)& \\ &3\vec{v} - 2\vec{w} = (6,9) - (2,-2) = (4,11)& \end{align*} $$
Le vecteur résultant \((4,11)\) est une combinaison linéaire de \( \vec{v} \) et \( \vec{w} \) avec des coefficients \(3\) et \(-2\), respectivement.

La multiplication scalaire satisfait également plusieurs propriétés importantes:

• Distributivité: Pour tous les scalaires \(k\) et \(l\) et tout vecteur \( \vec{v} \), nous avons \( (k+l) \vec{v} = k \vec{v} + l \vec{v} \).
• Associativité: Pour tout scalaire \(k\) et tout vecteurs \( \vec{u} \) et \( \vec{v} \), nous avons \( k( \vec{u} + \vec{v} ) = k \vec{u} + k \vec{v} \).
• Compatibilité avec la multiplication: Pour tous les scalaires \(k\) et \(l\) et tout vecteur \( \vec{v} \), nous avons \( (kl) \vec{v} = k(l \vec{v}) \).

Ces propriétés font de la multiplication scalaire un outil utile pour manipuler et résoudre des systèmes d'équations linéaires.

Transport parallèle ☰

Le transport parallèle est un concept de géométrie différentielle qui décrit comment un vecteur ou un espace tangent le long d'une courbe peut être transporté le long de la courbe sans changer sa direction. C'est un concept important pour comprendre la géométrie des espaces courbes.

En général, une courbe sur une variété est un chemin qui relie deux points sur la variété. Un vecteur tangent est un vecteur tangent à la courbe en un point particulier. Le transport parallèle le long d'une courbe est le processus de déplacement d'un vecteur tangent le long de la courbe tout en le maintenant tangent à la courbe à chaque point.

L'idée du transport parallèle est étroitement liée au concept de connexion sur une variété. Une connexion est une façon de relier les espaces tangents à différents points sur une variété. Elle permet de comparer les vecteurs tangents à différents points le long d'une courbe.

Pour définir le transport parallèle, il est nécessaire de spécifier une connexion sur la variété. Étant donné une connexion, le transport parallèle d'un vecteur le long d'une courbe est défini comme le vecteur unique qui est tangent à la courbe en chaque point et dont les composantes dans une base particulière restent constantes le long de la courbe.

Le concept de transport parallèle est important dans de nombreux domaines de la physique, notamment en relativité générale, où il est utilisé pour décrire le transport des tenseurs le long des trajectoires de l'espace-temps courbé.

Transformation et figures congruentes ☰

La transformation fait référence au processus de changement de la position, de la taille ou de la forme d'une figure géométrique. Il existe plusieurs types de transformations, notamment les translations, les réflexions, les rotations et les dilatations. Les figures congruentes sont des figures géométriques qui ont la même taille et la même forme, et leurs côtés et angles correspondants sont congruents.

Voici quelques théorèmes importants liés aux transformations et aux figures congruentes:

• Les parties correspondantes des figures congruentes sont congruentes (CPCTC): Ce théorème stipule que si deux figures sont congruentes, alors leurs côtés, angles et sommets correspondants sont congruents.
• La composition des translations est une translation: Si deux translations sont effectuées l'une après l'autre, alors la transformation résultante est également une translation.
• La composition des réflexions est une rotation ou une translation: Si deux réflexions sont effectuées l'une après l'autre, alors la transformation résultante est soit une rotation soit une translation.
• La composition des rotations est une rotation: Si deux rotations sont effectuées l'une après l'autre, alors la transformation résultante est également une rotation.
• La composition d'une dilatation et d'une translation est une dilatation: Si une dilatation et une translation sont effectuées l'une après l'autre, alors la transformation résultante est également une dilatation.
• La composition d'une dilatation et d'une rotation est une dilatation ou une rotation: Si une dilatation et une rotation sont effectuées l'une après l'autre, alors la transformation résultante est soit une dilatation soit une rotation.
• La composition de deux transformations congruentes est une transformation congruente: Si deux transformations sont congruentes, alors leur composition est également congruente.

Ces théorèmes sont importants pour comprendre les propriétés des transformations et des figures congruentes, et ils peuvent être utilisés pour prouver divers théorèmes géométriques et résoudre des problèmes en géométrie.