Introduction aux solides courbes
Classification des solides courbes
- Solides convexes
- Solides où tout segment de droite reliant deux points à l'intérieur du solide reste entièrement à l'intérieur du solide. Exemples : sphères, cônes et cylindres.
- Solides non convexes
- Solides où certains segments de droite reliant des points internes peuvent se situer partiellement à l'extérieur du solide. Exemples : tores et polyèdres concaves.
Théorèmes fondamentaux
- Théorème du centre de gravité de Pappus
- Énonce que le volume d’un solide de révolution est égal au produit de l’aire de la figure génératrice et de la longueur du chemin de rotation de son centre de gravité.
- Principe de Cavalieri
- Si deux solides ont la même hauteur et des aires de section transversale égales à chaque hauteur, leurs volumes sont égaux.
Propriétés de la géométrie sphérique
- Lignes parallèles : Inexistantes en géométrie sphérique
- Angles des triangles : La somme dépasse 180 degrés
- Calcul de l'aire : Proportionnel à l'angle excédentaire
Sphère
Un solide parfaitement symétrique où tous les points de surface sont équidistants du centre.
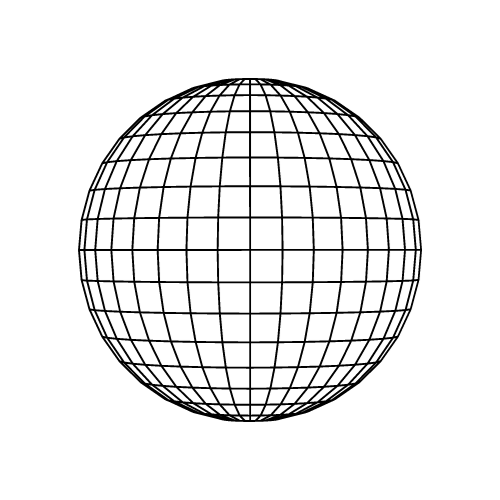
Formules clés
- Aire de surface
- \(SA = 4\pi r^2\)
- Volume
- \(V = \frac{4}{3}\pi r^3\)
- Diamètre
- \(D = 2r\)
Propriétés
- Distance égale du centre à tous les points de la surface
- Surface minimale pour un volume donné
- Symétrie infinie
- Ratio volume/surface optimal
Applications pratiques
- Corps célestes : Les forces gravitationnelles créent des planètes approximativement sphériques
- Gouttelettes de liquide : La tension de surface forme des formes sphériques
- Réservoirs sous pression : Réservoirs sphériques pour une répartition optimale de la pression
Cône
Un solide formé en reliant tous les points d'une base plane à un seul point sommet.
Formules essentielles
- Aire latérale
- \(S_{LSA} = \pi rl\)
- Aire totale
- \(S_{SA} = \pi r(r+l)\)
- Volume
- \(V = \frac{1}{3}\pi r^2h\)
- Hauteur oblique
- \(l = \sqrt{r^2 + h^2}\)
Tronc de cône
Une section de cône formée par des coupes parallèles à la base.
\(V = \frac{1}{3}\pi h(R^2 + r^2 + Rr)\)
Cylindre
Un solide avec des bases parallèles et congruentes connectées par une surface courbe.
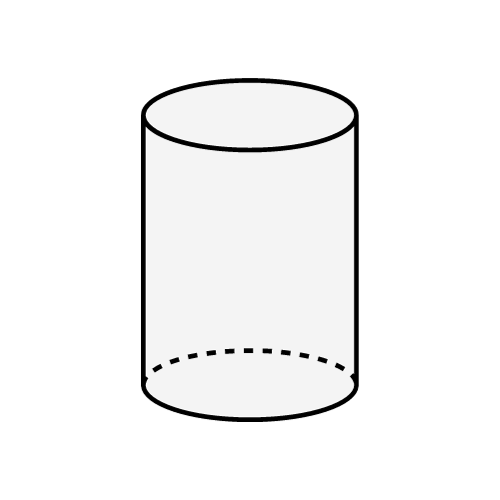
Formules principales
- Aire de surface
- \(SA = 2\pi r^2 + 2\pi rh\)
- Aire latérale
- \(LSA = 2\pi rh\)
- Volume
- \(V = \pi r^2h\)
Types de cylindres
- Cylindre circulaire droit
- Base circulaire avec un axe perpendiculaire
- Cylindre elliptique
- Base elliptique avec formule de volume : \(V = \pi abh\)
Applications
- Ingénierie : Tuyaux, colonnes, réservoirs de stockage
- Optique : Lentilles cylindriques pour corriger l'astigmatisme
- Architecture : Supports structurels et éléments décoratifs