Fonction quadratique et son graphique
Une fonction quadratique est une fonction polynomiale de degré deux. Elle est définie par la formule: \( f(x)=ax^2+bx+c \), où \(a\), \(b\) et \(c\) sont des constantes, et \(a\) est différent de zéro.
Le graphique d'une fonction quadratique est une parabole, qui est une courbe en forme de U. La direction de la parabole dépend du signe du coefficient principal \(a\). Si \(a\) est positif, la parabole s'ouvre vers le haut, et si \(a\) est négatif, la parabole s'ouvre vers le bas.
Le sommet de la parabole est donné par la formule: \(\left(-\frac{b}{2a}, \frac{4ac - b^2}{4a}\right)\).
L'axe de symétrie de la parabole est la ligne verticale passant par le sommet, donnée par l'équation \(x=-\frac{b}{2a}\).
Les intercepts \(x\) (zéros) de la fonction quadratique sont donnés par la formule quadratique: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
Si le discriminant \(b^2-4ac\) est positif, la fonction quadratique a deux racines réelles distinctes, qui sont les coordonnées \(x\) des intercepts \(x\). Si le discriminant est nul, la fonction quadratique a une seule racine réelle, qui est la coordonnée \(x\) du sommet. Si le discriminant est négatif, la fonction quadratique n'a pas de racines réelles, mais deux
racines complexes conjuguées.
Les fonctions quadratiques peuvent également être écrites sous forme factorisée: \( f(x)=a(x-r_1 )(x-r_2 ) \), où \(r_1\) et \(r_2\) sont les racines de la fonction quadratique. Cette forme est utile pour trouver les racines de la fonction.
La forme de sommet de la fonction quadratique est: \( f(x)=a(x-h)^2 +k \), où \( (h,k) \) est le sommet de la parabole. La forme standard et la forme de sommet de la fonction quadratique sont liées par : \( f(x)=a(x-h)^2 +k=ax^2 -2ahx+ah^2 +k \), ce qui montre que \(a\), \( b=-2ah \), et \( c=ah^2 +k\) sont liés au sommet \( (h,k) \).
La fonction quadratique peut être tracée en traçant le sommet, l'axe de symétrie et les intercepts \(x\). Pour esquisser le graphique, nous pouvons également trouver la valeur maximale ou minimale de la fonction, le domaine, la portée et toutes les transformations ou déplacements.
Valeur maximale ou minimale
de la fonction quadratique:
Si \( a > 0 \), la parabole s'ouvre vers le haut, et le sommet est le point de minimum de la fonction. La valeur minimale est \( f(h)=k \). Si \( a < 0 \), la parabole s'ouvre vers le bas, et le sommet est le point de maximum de la fonction. La valeur maximale est \(f(h)=k\).
Domaine et portée
de la fonction quadratique:
Le domaine de la fonction quadratique est l'ensemble de tous les nombres réels, puisque la fonction est définie pour toutes les valeurs de \(x\). La portée dépend du signe du coefficient principal \(a\). Si \(a>0\), la portée est \( \left [k, \infty \right ) \) et si \(a < 0 \), la portée est \( \left ( - \infty ,k \right ] \).
Graphique:
Le graphique d'une fonction quadratique peut être transformé en modifiant les valeurs de \(a\), \(b\) et \(c\). Par exemple, si \(a\) est multiplié par une constante positive, le graphique est étiré verticalement, et si \(a\) est multiplié par une constante négative, le graphique est réfléchi par rapport à l'axe \(x\). Si \(b\) est ajouté ou soustrait de \(x\), le
graphique est déplacé horizontalement et si \(c\) est ajouté ou soustrait de \(f(x)\), le graphique est déplacé verticalement.

Fonction Valeur Absolue (y=|x|) et son graphique
La fonction \( f(x)=|x| \) est une fonction définie par morceaux qui prend la valeur absolue de l'entrée \(x\). La fonction valeur absolue est définie comme suit:
\( | x | = \begin{cases} -x & \text{, } x < 0 \\ x & \text{, } x \geq 0 \end{cases} \)
Par conséquent, la fonction \(f(x)=|x|\) prend la valeur \(x\) lorsque \(x\) est non négatif, et \(-x\) lorsque \(x\) est négatif. Le graphique de \( f(x)=|x| \) est une courbe en forme de V avec le sommet à l'origine. La pente de la courbe change à \(x=0\), où la fonction n'est pas différentiable.
Voici quelques propriétés importantes de la fonction valeur absolue:
Symétrie:
La fonction \(f(x)=|x|\) est symétrique par rapport à l'origine, ce qui signifie que \(f(x)=f(-x) \) pour tous \(x\).
Valeurs non négatives:
La valeur absolue de tout nombre réel est non négative, ce qui signifie que \( |x| \ge 0 \) pour tous \(x\).
Distance:
La valeur absolue d'un nombre représente sa distance par rapport à zéro sur la droite numérique. Par exemple, \(|3|=3\) et \(|-5|=5\).
Fonction définie par morceaux:
La fonction valeur absolue est une fonction définie par morceaux, ce qui signifie qu'elle est définie différemment pour différents intervalles de l'entrée \(x\). En particulier, \(f(x)=x\) lorsque \(x \ge 0 \) et \( f(x)=-x \) lorsque \(x < 0 \).
Applications:
La fonction valeur absolue est utilisée dans diverses applications, telles que la mesure de la différence entre deux valeurs, le calcul des distances et la résolution des équations de valeur absolue.
Graphique:

En résumé, la fonction valeur absolue est une fonction définie par morceaux qui prend la valeur non négative de son entrée si elle est non négative, et le négatif de son entrée si elle est négative. Le graphique de \(f(x)=|x| \) est une courbe en forme de V qui est symétrique par rapport à l'origine.
Fonction cubique et son graphique
La fonction \(f(x)=x^3\) est une fonction cubique qui prend l'entrée \(x\) et l'élève à la puissance trois. Le graphique de \(f(x)=x^3\) est une courbe qui passe par l'origine et a une forme similaire à la lettre "S". La fonction est définie pour toutes les valeurs réelles de \(x\).
Voici quelques propriétés importantes de la fonction cubique:
Domaine et image:
Le domaine de la fonction \(f(x)=x^3\) est l'ensemble des nombres réels, ce qui signifie que n'importe quel nombre réel peut être substitué dans la fonction. L'image de la fonction est également l'ensemble des nombres réels, ce qui signifie que la sortie peut prendre n'importe quelle valeur réelle.
Symétrie:
La fonction \(f(x)=x^3\) est une fonction impaire, ce qui signifie que \(f(-x)=-f(x)\) pour tous \(x\). Cette propriété résulte en ce que le graphique de la fonction soit symétrique par rapport à l'origine.
Interceptions:
La fonction \(f(x)=x^3\) passe par l'origine, ce qui signifie qu'elle a une ordonnée à l'origine de zéro. La fonction n'a pas d'abscisses à l'origine.
Intervalles de croissance et de décroissance:
La fonction \(f(x)=x^3\) est croissante pour tout \(x\), ce qui signifie que la valeur de la fonction augmente lorsque \(x\) augmente. Cette propriété résulte en ce que le graphique de la fonction soit en pente ascendante. La fonction n'a pas de maximums locaux ou de minimums locaux.
Applications:
La fonction cubique est utilisée dans diverses applications, telles que la modélisation du volume d'un cube ou la croissance d'une population.
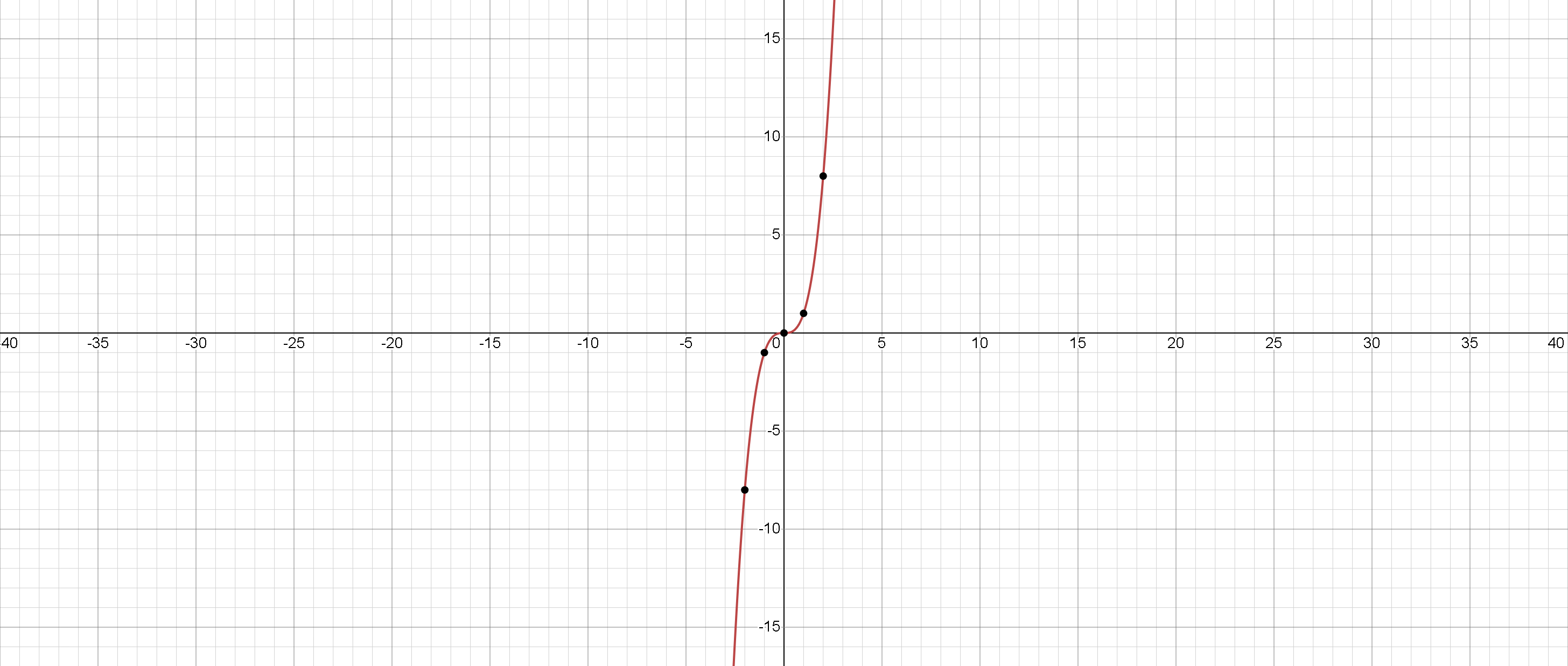
En résumé, la fonction cubique \(f(x)=x^3\) est une fonction qui élève l'entrée \(x\) à la puissance trois. Le graphique de la fonction est une courbe en pente ascendante qui passe par l'origine et est symétrique par rapport à l'origine. La fonction est définie pour toutes les valeurs réelles de \(x\) et a une image de tous les nombres réels.