Domaine et Plage de fonctions ☰

Une fonction est un objet mathématique qui attribue une sortie unique à chaque entrée. L'ensemble de toutes les entrées possibles est appelé le domaine de la fonction, et l'ensemble de toutes les sorties possibles est appelé la plage de la fonction. En d'autres termes, le domaine est l'ensemble des valeurs qui peuvent être entrées dans la fonction, et la plage est l'ensemble des valeurs que la fonction peut produire.
Formellement, une fonction \(f\) est une correspondance d'un ensemble \(A\) (le domaine) à un ensemble \(B\) (la plage), où pour chaque \( a \in A\) , il existe un unique \( b \in B \) tel que \(f(a)=b \). On écrit \(f\): \( A \rightarrow B \) pour indiquer que \(f\) est une fonction de \(A\) à \(B\).
Par exemple, considérons la fonction \(f(x)=x^2\), où \(x\) est un nombre réel. Le domaine de \(f\) est l'ensemble de tous les nombres réels, car n'importe quel nombre réel peut être inséré dans \(f\). Cependant, la plage de \(f\) est seulement l'ensemble des nombres réels non négatifs, car \(f(x)\) est toujours non négatif.
Lorsque l'on trouve le domaine et la plage d'une fonction, il y a quelques points à garder à l'esprit:

• Le domaine d'une fonction est l'ensemble de toutes les entrées possibles. Cela signifie que toute valeur qui rend la fonction indéfinie (comme diviser par zéro ou prendre la racine carrée d'un nombre négatif) ne peut pas être dans le domaine.
• La plage d'une fonction est l'ensemble de toutes les sorties possibles. Cela signifie que la fonction ne peut produire que des valeurs qui sont dans la plage.
• Il est possible que différentes fonctions aient le même domaine ou la même plage. Par exemple, les fonctions \(f(x)=x^2 \) et \(g(x)=|x| \) ont toutes deux le domaine de tous les nombres réels, mais leurs plages sont différentes.
• Le domaine et la plage d'une fonction peuvent être déterminés en analysant le graphique de la fonction. Le domaine est l'ensemble de toutes les valeurs \(x\) possibles qui apparaissent sur le graphique, et la plage est l'ensemble de toutes les valeurs \(y\) possibles qui apparaissent sur le graphique.

Regardons quelques exemples pour mieux comprendre comment trouver le domaine et la plage d'une fonction.

Exemple 1: Trouver le domaine et la plage de la fonction \( f(x) = \frac{1}{x} \)
La fonction \(f(x) \) est définie pour tous les \( x \neq 0 \) car la division par zéro est indéfinie. Par conséquent, le domaine de \(f\) est l'ensemble de tous les nombres réels sauf zéro, soit \( (-\infty ; 0) \cup (0 ; \infty ) \).
Pour trouver la plage de \(f\), notons que \(f(x) \) peut être n'importe quel nombre réel sauf zéro. Cela signifie que la plage de \(f\) est également \( (-\infty ; 0 ) \cup ( 0 ; \infty ) \).

Exemple 2: Trouver le domaine et la plage de la fonction \( f(x) = \sqrt{4-x^2} \).
La fonction \(f(x)\) est définie uniquement pour les valeurs de \(x\) telles que \( 4 - x^2 \ge 0 \). En résolvant cette inégalité, nous obtenons \( -2 \le x \le 2 \).
Par conséquent, le domaine de \(f\) est l'intervalle fermé \([-2,2]\). Pour trouver la plage de \(f\), notons que \(f(x)\) peut être n'importe quel nombre réel non négatif inférieur ou égal à 2. Cela signifie que la plage de \(f\) est l'intervalle fermé \([0,2]\).

Exemple 3: Trouver le domaine et la plage de la fonction \(f(x)=sin(x) \).
La fonction \(f(x) \) est définie pour tous les nombres réels, donc le domaine de \(f\) est \( (-\infty , \infty) \).
Pour trouver la plage de \(f\), notons que \(sin(x)\) peut prendre n'importe quelle valeur entre -1 et 1, inclusivement. Par conséquent, la plage de \(f\) est l'intervalle fermé \([-1,1] \).

En résumé, le domaine d'une fonction est l'ensemble de toutes les entrées possibles, et la plage est l'ensemble de toutes les sorties possibles. Le domaine et la plage peuvent être déterminés en analysant la fonction elle-même ou son graphique.

Propriétés des fonctions ☰

Les fonctions ont diverses propriétés qui peuvent être utilisées pour les analyser et les comparer. Dans cette explication, nous discuterons de certaines des propriétés les plus importantes des fonctions.

Fonctions paires et impaires:
Une fonction \(f\) est dite paire si \(f(-x)=f(x) \) pour tous \(x\) dans le domaine de \(f\). En d'autres termes, la fonction est symétrique par rapport à l'axe des \(y\). Un exemple de fonction paire est \(f(x)=x^2 \).
Une fonction \(f\) est dite impaire si \(f(-x)=-f(x) \) pour tous \(x\) dans le domaine de \(f\). En d'autres termes, la fonction est symétrique par rapport à l'origine. Un exemple de fonction impaire est \(f(x)=x^3 \).

Fonctions croissantes et décroissantes:
Une fonction \(f\) est dite croissante sur un intervalle si \( f(x_1 ) < f(x_2 ) \) chaque fois que \(x_1 < x_2\) et \(x_1, x_2 \) sont dans le domaine de \(f\). En d'autres termes, la fonction augmente lorsque \(x\) augmente. Un exemple de fonction croissante est \(f(x)=x \).
Une fonction \(f\) est dite décroissante sur un intervalle si \( f(x_1 ) > f(x_2 ) \) chaque fois que \(x_1 < x_2\) et \(x_1, x_2 \) sont dans le domaine de \(f\). En d'autres termes, la fonction diminue lorsque \(x\) augmente. Un exemple de fonction décroissante est \(f(x)=-x \).

Fonctions périodiques:
Une fonction \(f\) est dite périodique s'il existe un nombre positif \(p\) tel que \(f(x+p)=f(x)\) pour tous \(x\) dans le domaine de \(f\). En d'autres termes, la fonction se répète après un intervalle fixe. Un exemple de fonction périodique est \(f(x)=sin(x)\).

Fonctions injectives et surjectives:
Une fonction \(f\) est dite injective (ou bijective) si pour chaque \(y\) dans la plage de \(f\), il existe exactement un \(x\) dans le domaine de \(f\) tel que \(f(x)=y\). En d'autres termes, aucun deux entrées distinctes ne donnent la même sortie. Un exemple de fonction injective est \( f(x)=x+1 \).
Une fonction \(f\) est dite surjective (ou surjective) si pour chaque \(y\) dans la plage de \(f\), il existe au moins un \(x\) dans le domaine de \(f\) tel que \(f(x)=y\). En d'autres termes, chaque sortie de la plage est obtenue par une certaine entrée. Un exemple de fonction surjective est \( f(x)=x^2 \).

Fonctions bijectives:
Une fonction \(f\) est dite bijective si elle est à la fois injective et surjective. En d'autres termes, chaque sortie de la plage est obtenue par exactement une entrée. Un exemple de fonction bijective est \( f(x)= \sqrt{x} \).

En résumé, les propriétés des fonctions peuvent être utilisées pour décrire divers aspects de la fonction, tels que sa symétrie, sa direction, sa répétition et sa correspondance entre les entrées et les sorties. Comprendre ces propriétés peut aider à analyser et comparer les fonctions dans différents contextes.

Classification des fonctions ☰

Les fonctions peuvent être classées en fonction de leurs propriétés et de leur comportement. Dans cette explication, nous discuterons des classifications les plus courantes des fonctions.

Fonction constante:
\(F(x) = c.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = \{c\}.\)


Fonction linéaire:
\(F(x) = x.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Zéros: \( x=0 \).
Fonction croissante.
Aucun extremum.


Fonction valeur absolue:
\(F(x) = |x|.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = [0, +\infty).\)
Zéros: \(x = 0.\)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Point minimum: \((0, 0).\)


Fonction rationnelle:
\(F(x) = \frac{1}{x}.\)
\(D(f) = (-\infty, 0) \cup (0, +\infty).\)
\(E(f) = (-\infty, 0) \cup (0, +\infty).\)
\((- \infty, 0) \downarrow \text{, } (0, +\infty) \downarrow.\)
Pas de zéros.
Aucun extremum.


Fonction quadratique:
\(F(x) = x^2.\)
\( D(f) = (-\infty, +\infty). \)
\( E(f) = [0, +\infty). \)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Zéros : \(x = 0.\)
Point minimum: \((0, 0).\)


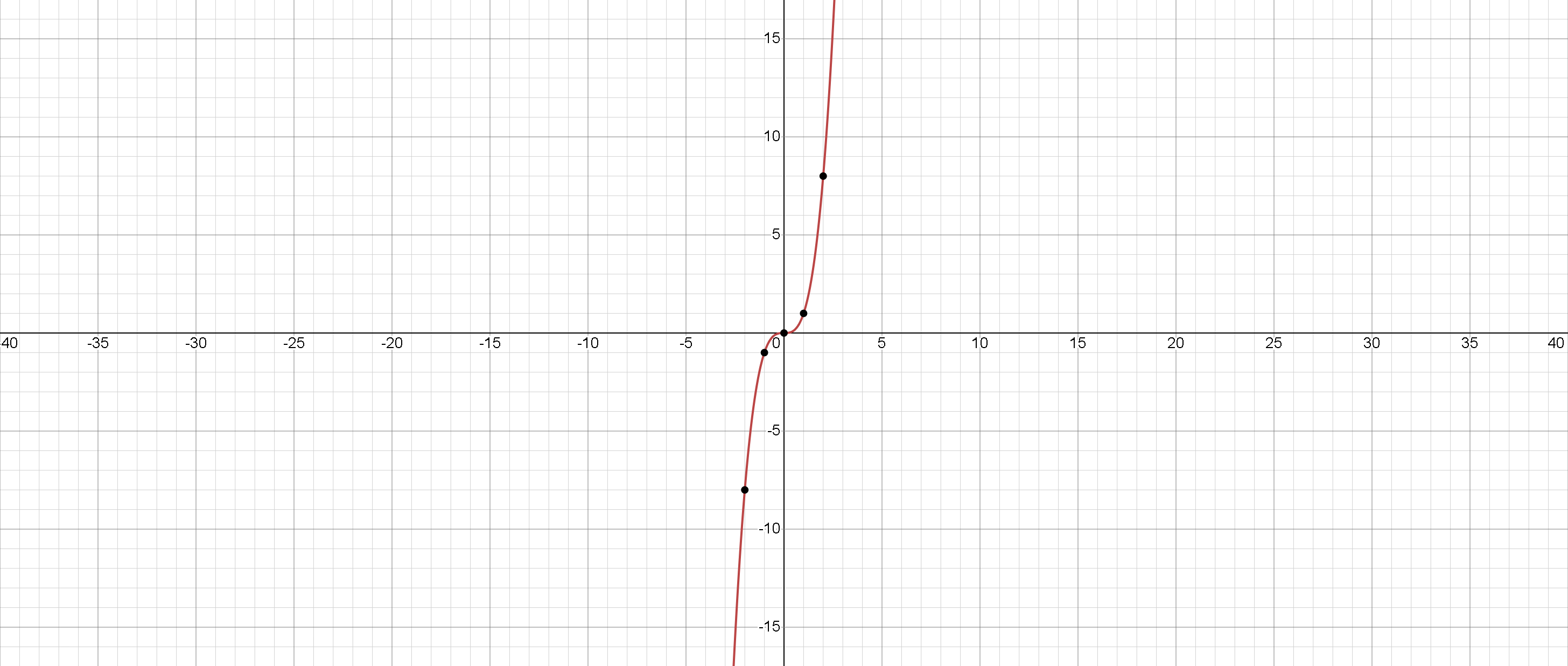
Fonction cubique :
\(F(x) = x^3.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Zéros: \(x = 0.\)
Fonction croissante.
Aucun extremum.


Fonction racine carrée :
\(F(x) = \sqrt{x}.\)
\(D(f) = [0; +\infty).\)
\(E(f) = [0; +\infty).\)
Zéros: \(x = 0.\)
\( [0; +\infty) \uparrow \).
Aucun extremum.


Fonctions trigonométriques :
Une fonction trigonométrique est une fonction qui implique les rapports des côtés d'un triangle rectangle. Des exemples de fonctions trigonométriques incluent \( sin(x) \), \( cos(x) \) et \( tan(x) \). Les graphiques des fonctions trigonométriques sont périodiques et se répètent après un intervalle fixe.

Fonctions morceaux par morceaux:
Une fonction morceau par morceau est une fonction qui est définie par différentes équations sur différentes parties de son domaine.

Des exemples de fonctions morceau par morceau incluent:
\( f(x) = \begin{cases} 2x + 1 & \text{si } x < 0 \\ 3x & \text{si } x \geq 0 \end{cases} \)

\( f(x) = \begin{cases} x^2 & \text{si } x \leq -1 \\ -x & \text{si } -1 < x < 1 \\ x & \text{si } x \geq 1 \end{cases} \)

Fonctions puissance ou monômes ☰

Ces fonctions sont également connues sous le nom de fonctions puissance ou monômes.
La valeur de l'exposant \(n\) détermine la forme et le comportement de la fonction. Lorsque \(n\) est un entier positif, la fonction représente un polynôme avec un seul terme, appelé monôme. Le degré du polynôme est égal à la valeur de \(n\).

\( F(x)= x^{2k} \):
\( D(f) = (-\infty ; +\infty) \).
\( E(f) = [0; +\infty). \)
Zéros: \(x=0 \).
\( (-\infty; 0] \downarrow \text{, } [0; +\infty) \uparrow \).
\( x_{\text{min}} = 0, f_{\text{min}} = 0 \).
Aucun extremum.

\( F(x) = x^{2k+1} \):
\( D(f) = (-\infty ; +\infty). \)
\( E(f) = (-\infty ; +\infty). \)
Zéros: \( x=0 \).
\( (-\infty ; +\infty) \uparrow \)
Aucun extremum.

Par exemple, la fonction \(y=x^2\) représente une parabole, qui est une courbe en forme de U qui s'ouvre vers le haut. Cette fonction a une valeur minimale à \(x=0\) et augmente indéfiniment lorsque \(x\) s'éloigne de zéro dans n'importe quelle direction.
Lorsque \(k\) est un entier négatif, la fonction représente le réciproque d'un monôme. Par exemple, la fonction \(y = x^{-1} \) représente la fonction réciproque, également appelée fonction inverse. Cette fonction a une asymptote verticale à \(x=0\), où la fonction tend vers l'infini positif ou négatif selon le signe de \(x\). La fonction réciproque est symétrique par rapport à la ligne \(y=x\).
Lorsque \(2k =n\) ou \(2k+1 = n\) est une fraction, la fonction représente une fonction radicale, où le numérateur de la fraction détermine le degré de la racine et le dénominateur détermine la puissance de \(x\). Par exemple, la fonction \( y = x^\frac{1}{2} \) représente la fonction racine carrée, qui a un domaine de nombres réels non négatifs et une plage de nombres réels non négatifs. La fonction racine carrée est une demi-parabole qui s'ouvre vers la droite et a une asymptote verticale à \(x=0\).
En général, la famille de fonctions \(y=x^n\) présente une variété de comportements en fonction de la valeur de \(n\). Le graphique de ces fonctions peut avoir différentes formes, y compris des lignes, des courbes et des sauts discontinus. L'étude de ces fonctions est importante en mathématiques et en sciences, car elles apparaissent dans de nombreux phénomènes naturels et applications d'ingénierie.

Quelques propriétés importantes de ces fonctions incluent:

• Lorsque \(n\) est pair, la fonction \(y=x^n\) est toujours non négative pour toutes les valeurs réelles de \(x\). Lorsque \(n\) est impair, la fonction peut prendre des valeurs positives et négatives selon le signe de \(x\).
• Lorsque \(n\) est positif, la fonction \(y=x^n\) est croissante sur l'intervalle \( (0, \infty) \) et décroissante sur l'intervalle \( (-\infty, 0) \). Lorsque \(n\) est négatif, la fonction a le comportement opposé.
• La dérivée de la fonction \(y=x^n\) est donnée par \( y'=nx^{n-1} \). Cela signifie que la pente de la tangente à la fonction en tout point est proportionnelle à la valeur de l'exposant \(n\).
• L'intégrale de la fonction \(y=x^n\) est donnée par \( \int x^n \, dx = \frac{x^{(n+1)}}{(n+1)} + C \), où \(C\) est une constante d'intégration. Cette formule est valable pour toutes les valeurs de \(n\) sauf lorsque \(n=-1\), auquel cas l'intégrale est donnée par \( ln|x|+C \).

En résumé, la famille de fonctions \(y=x^n\) est un sujet fondamental en mathématiques, avec de nombreuses applications importantes dans divers domaines. Le comportement et les propriétés de ces fonctions dépendent de la valeur de l'exposant \(n\), qui détermine la forme du graphique et d'autres caractéristiques importantes.

Opérations sur les fonctions ☰

En mathématiques, les opérations sur les fonctions désignent les opérations mathématiques qui peuvent être effectuées sur des fonctions. Ces opérations peuvent être utilisées pour manipuler ou combiner des fonctions afin de créer de nouvelles fonctions. Les opérations les plus courantes sur les fonctions comprennent l'addition, la soustraction, la multiplication, la division, la composition et l'inverse.

Addition et Soustraction des Fonctions:
Les fonctions peuvent être additionnées ou soustraites pour créer une nouvelle fonction. Étant données deux fonctions \(f(x)\) et \(g(x)\), la somme ou la différence des deux fonctions est notée \( (f \pm g)(x) \) et est définie comme suit:
\( (f+g) (x) = f(x)+ g(x) \)
\( (f-g) (x) = f(x)- g(x) \)
La somme de deux fonctions paires est paire, et la somme de deux fonctions impaires est impaire.

Par exemple: \( f(x) = x+1 \) et \( g(x) = 2x-3 \) fonctions.
\( \small (f+g) (x) = f(x) + g(x) = (x+1) + (2x-3) =\) \( 3x-2 \)
\( \small (f-g) (x) = f(x) - g(x) = (x+1) - (2x-3) =\) \( -x+4 \)

Multiplication et Division des Fonctions:
Les fonctions peuvent également être multipliées ou divisées pour créer de nouvelles fonctions. Étant données deux fonctions \(f(x)\) et \(g(x)\), le produit ou le quotient des deux fonctions est noté \( (f \cdot g) (x) \) ou \( (\frac{f}{g}) (x) \) et est défini comme suit:
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( ( \frac{f}{g} )(x) = \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \)

Le produit (le quotient) de deux fonctions paires et de deux fonctions impaires est une fonction paire, et le produit (le quotient) d'une fonction paire et d'une fonction impaire est une fonction impaire.

Par exemple: \( f(x) = x+1 \) et \( g(x) = 2x-3 \) fonctions.
\( (f \cdot g)(x) = (x+1)(2x-3) = 2x^2 - x - 3 \)
\( (\frac{f}{g})(x) = \frac{x+1}{2x-3} \)

Composition des Fonctions:
La composition des fonctions est l'opération de combinaison de deux fonctions ou plus pour créer une nouvelle fonction. Étant données deux fonctions \( f(x) \) et \( g(x) \), la composition des deux fonctions est notée \( (f \circ g)(x) \) et est définie comme suit: \( (f \circ g)(x) = f(g(x)) \).

Par exemple: \( f(x) = x^2 \) et \( g(x) = x+1 \) fonctions.
\( (f \circ g) (x) = f(g (x) ) = f(x+1) = (x+1)^2 \)
Notez que l'ordre de la composition est important, c'est-à-dire que \( (f \circ g)(x) \) n'est pas la même chose que \( (g \circ f)(x) \).

Inverse d'une Fonction :
L'inverse d'une fonction est une nouvelle fonction qui "défait" la fonction d'origine. Étant donnée une fonction \(f(x) \), l'inverse de la fonction est noté \(f^{-1} (x) \) et est défini comme suit:
\( f^{-1} (f(x)) = x \)

Pour que l'inverse d'une fonction existe, la fonction doit être bijective. Une fonction est bijective si chaque élément du domaine est associé à un élément unique de l'ensemble d'arrivée. La fonction inverse est la réflexion de la fonction par rapport à la droite \(y=x\).
Par exemple: Si \( f(x) = 2x+1 \) , alors \( f^{-1} (x) = \frac{x-1}{2} \)
Pour le vérifier, nous pouvons vérifier que \( f^{-1} (f(x))= \frac{2x+1-1}{2} = x \).

Voici quelques détails supplémentaires sur les opérations sur les fonctions:

Propriétés des Opérations sur les Fonctions:
Les opérations sur les fonctions ont certaines propriétés qui les rendent utiles pour résoudre des problèmes mathématiques. Ces propriétés comprennent:

• Associativité: L'ordre dans lequel les opérations sont effectuées n'affecte pas le résultat.
  Par exemple, \( (f+g)+h = f+(g+h) \)
• Commutativité: L'ordre des fonctions n'affecte pas le résultat.
  Par exemple, \( f+g=g+f \)
• Distributivité: L'opération se distribue sur une autre opération.
  Par exemple, \( f \cdot (g+h) = f \cdot g + f \cdot h \)

Domaines et Plages:
Lorsque l'on effectue des opérations sur des fonctions, il est important de prendre en compte les domaines et les plages des fonctions. Le domaine d'une fonction est l'ensemble des valeurs pour lesquelles la fonction est définie, tandis que la plage est l'ensemble des valeurs que la fonction peut prendre.
Lorsque l'on ajoute ou soustrait des fonctions, les domaines et les plages des fonctions doivent être les mêmes. Lorsque l'on multiplie ou divise des fonctions, le domaine de la fonction résultante doit être l'intersection des domaines des deux fonctions, et la plage de la fonction résultante peut être restreinte par la plage du dénominateur.
Lorsque l'on compose des fonctions, la plage de la fonction interne doit être un sous-ensemble du domaine de la fonction externe.

Transformations des Fonctions:
Les opérations sur les fonctions peuvent également être utilisées pour transformer des fonctions. Par exemple, ajouter une constante à une fonction déplace la fonction verticalement, tandis que multiplier une fonction par une constante met à l'échelle la fonction verticalement. De même, ajouter une variable à une fonction déplace la fonction horizontalement, tandis que multiplier une fonction par une variable met à l'échelle la fonction horizontalement.