Polygones ☰

Un polygone est une figure géométrique bidimensionnelle qui se compose d'un nombre fini de segments de droite (appelés côtés ou arêtes) qui sont reliés bout à bout pour former une forme fermée. Le mot "polygone" vient des mots grecs "poly" (signifiant "beaucoup") et "gon" (signifiant "angle").
Les polygones peuvent avoir n'importe quel nombre de côtés, mais ils doivent être des lignes droites et ne peuvent pas se croiser. Les polygones à trois côtés sont appelés triangles, ceux à quatre côtés sont appelés quadrilatères, ceux à cinq côtés sont appelés pentagones, et ainsi de suite.
Le périmètre d'un polygone est la somme des longueurs de ses côtés. Si un polygone a \(n\) côtés et que la longueur de chaque côté est notée \(s_i\) pour \(i = 1,2,…,n,\) alors le périmètre \(P\) est donné par:
\( P = s_1 + s_2 + \ldots + s_n = \sum_{i=1}^n s_i\)

Les angles intérieurs d'un polygone sont les angles formés par deux côtés adjacents à l'intérieur du polygone. La somme des angles intérieurs d'un polygone à \(n\) côtés est donnée par la formule:
\( \sum_{i=1}^n \theta_i =(n-2) \cdot 180^\circ \) , où \( \theta_i \) est la mesure du \(i-ème\) angle intérieur en degrés.

Les polygones réguliers sont des polygones dans lesquels tous les côtés ont la même longueur et tous les angles intérieurs ont la même mesure. La mesure de chaque angle intérieur d'un polygone régulier à \(n\) côtés est donnée par:
\( \theta = \frac{(n-2) \cdot 180^\circ }{n} \) .

La surface d'un polygone peut être calculée de plusieurs manières, selon la forme du polygone.
Par exemple, la surface d'un triangle peut être calculée à l'aide de la formule: \( A = \frac{1}{2} bh \) , où \(b\) est la base du triangle et \(h\) est sa hauteur.
La surface d'un polygone régulier à \(n\) côtés et de longueur de côté \(s\) peut être calculée à l'aide de la formule: \( A= \frac{1}{4} ns^2 cot(\frac{\pi }{n}) \), où \(cot(x)\) est la fonction cotangente.

Les polygones sont utilisés dans de nombreux domaines différents, notamment en mathématiques, en ingénierie et en infographie. Ils sont également utilisés dans la vie quotidienne, comme dans la conception de bâtiments et de meubles.

Polygones convexes et concaves ☰

Les polygones peuvent être classés comme convexes ou concaves en fonction de la nature de leurs angles.
Un polygone convexe est un polygone dans lequel tous ses angles intérieurs sont inférieurs à 180 degrés. En d'autres termes, si vous tracez un segment de droite entre deux points à l'intérieur du polygone, le segment se trouvera toujours entièrement à l'intérieur du polygone. De manière équivalente, un polygone convexe est un polygone qui ne "se courbe pas vers l'intérieur" comme une cuillère.
Des exemples de polygones convexes comprennent les triangles équilatéraux, les carrés, les pentagones réguliers et les hexagones réguliers. Les polygones convexes sont importants dans de nombreux domaines des mathématiques et des applications, car ils ont de nombreuses propriétés utiles et sont relativement faciles à manipuler.
En revanche, un polygone concave est un polygone dans lequel au moins un de ses angles intérieurs est supérieur à 180 degrés. En d'autres termes, si vous tracez un segment de droite entre deux points à l'intérieur du polygone, le segment croisera la frontière du polygone. De manière équivalente, un polygone concave est un polygone qui "se courbe vers l'intérieur" comme une cuillère.
Des exemples de polygones concaves comprennent la lettre "C" (lorsqu'elle est dessinée comme une forme fermée), la lettre "L" et tout polygone avec une "encoche" ou une "entaille" dans sa frontière. Les polygones concaves sont moins courants dans les applications, car ils ont une géométrie plus compliquée et peuvent être plus difficiles à manipuler mathématiquement.
Une différence importante entre les polygones convexes et concaves est que les polygones convexes ont un point central unique appelé le centroïde, qui est également le centre de gravité ou d'équilibre du polygone. Cela rend les polygones convexes utiles dans des applications telles que l'ingénierie et l'architecture, où l'équilibre et la stabilité sont des facteurs importants. En revanche, les polygones concaves n'ont pas de centroïde unique, ce qui les rend plus difficiles à analyser et à manipuler.

La somme des angles intérieurs d'un polygone convexe ☰

La somme des angles intérieurs d'un polygone convexe avec \(n\) côtés est donnée par la formule: \( \sum_{i=1}^n \theta_i =(n-2)⋅180^\circ \), où \( \theta_i\) est la mesure de l'angle intérieur \(i\) en degrés.
La somme des angles extérieurs d'un polygone convexe est toujours de 360 degrés, quel que soit le nombre de côtés. Cela signifie que si vous mesurez chaque angle extérieur d'un polygone convexe et que vous ajoutez les mesures, le total sera toujours de 360 degrés.
Pour comprendre pourquoi cela est vrai, imaginez-vous marcher autour du périmètre du polygone et tourner à chaque sommet pour suivre le côté suivant. À chaque tour, vous faites un angle extérieur avec le côté que vous venez de quitter. Si vous faites le tour complet du polygone, vous aurez tourné un total de 360 degrés.
Nous pouvons utiliser la formule de la somme des angles intérieurs et le fait que les angles extérieurs s'additionnent à 360 degrés pour trouver la mesure de chaque angle extérieur. Soit \(a_i\) la mesure du \(i\)-ème angle extérieur en degrés. Alors nous avons:

\( \sum_{i=1}^n \theta_i + \sum_{i=1}^n a_i =(n-2) \cdot 180^\circ +360^\circ \)

\( \small \sum_{i=1}^n a_i =(\sum_{i=1}^n \theta_i )-(n-2) \cdot 180^\circ +360^\circ = \) \( (n-2) \cdot 180^\circ -(n-2) \cdot 180^\circ +360^\circ=360^\circ \)

Par conséquent, la mesure de chaque angle extérieur d'un polygone convexe est donnée par: \( a_i= 360^\circ - \theta_i \).
Notez que cette formule s'applique uniquement aux polygones convexes, et non aux polygones concaves, qui peuvent avoir des angles extérieurs supérieurs à 180 degrés.

Polygones inscrits et circonscrits ☰

Les polygones inscrits et circonscrits sont des concepts importants en géométrie qui impliquent des polygones inscrits à l'intérieur et circonscrits autour d'un cercle. Ces concepts sont souvent utilisés dans divers domaines des mathématiques, tels que la géométrie, la trigonométrie et le calcul.

Polygone inscrit
Un polygone inscrit est un polygone dessiné à l'intérieur d'un cercle de telle sorte que tous ses sommets se trouvent sur la circonférence du cercle. La figure ci-dessous montre un exemple de polygone inscrit.


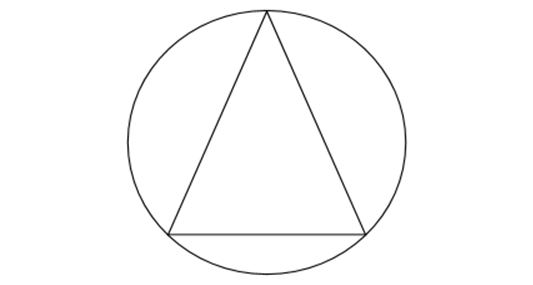
La propriété clé d'un polygone inscrit est que la somme des angles intérieurs est égale à \( (n-2) 180^\circ \), où \(n\) est le nombre de côtés du polygone. Cela est connu sous le nom de somme des angles intérieurs d'un polygone. Nous pouvons prouver cette propriété en utilisant le fait que l'angle central du cercle subtendu par chaque côté du polygone est égal à l'angle intérieur correspondant du polygone. Comme la somme des angles centraux est \( 360^\circ \) (l'angle complet du cercle), la somme des angles intérieurs doit être \( (n-2) 180^\circ \).
Une autre propriété importante d'un polygone inscrit est que le produit des longueurs de ses côtés est maximisé lorsque le polygone est un polygone régulier. Autrement dit, si \(s_1\), \(s_2\), … , \(s_n\) sont les longueurs des côtés d'un polygone inscrit à \(n\) côtés, alors le produit \(s_1\), \(s_2\), … , \(s_n\) est maximisé lorsque le polygone est un polygone régulier.

Polygone circonscrit
Un polygone circonscrit est un polygone dessiné à l'extérieur d'un cercle de telle sorte que tous ses sommets se trouvent sur la circonférence du cercle. La figure ci-dessous montre un exemple de polygone circonscrit.


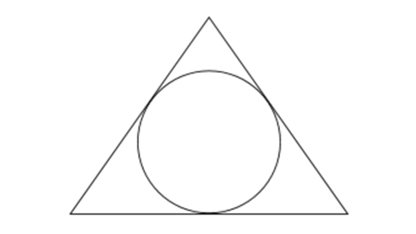
La propriété clé d'un polygone circonscrit est que le produit des longueurs de ses côtés est égal à \( 2R^n sin( \frac{360^\circ}{n} ) \), où \(n\) est le nombre de côtés du polygone et \(R\) est le rayon du cercle. Cela est connu sous le nom de formule du produit des côtés d'un polygone. Nous pouvons prouver cette formule en utilisant le fait que la longueur de chaque côté du polygone est égale à deux fois le rayon fois le sinus de la moitié de l'angle central du cercle subtendu par ce côté. Comme l'angle central d'un polygone régulier à \(n\) côtés est \( \frac{360^\circ}{n} \) , nous avons la formule ci-dessus.
Une autre propriété importante d'un polygone circonscrit est que la zone du polygone est maximisée lorsque le polygone est un polygone régulier. Autrement dit, si \(A\) est la zone d'un polygone circonscrit à \(n\) côtés, alors la zone est maximisée lorsque le polygone est un polygone régulier.

Exemples
Prenons un exemple pour illustrer ces concepts. Supposons que nous ayons un cercle de rayon 5. Quelle est l'aire maximale d'un pentagone inscrit (un polygone à cinq côtés) dans ce cercle, et quelle est l'aire maximale d'un pentagone circonscrit ?

Pour trouver l'aire maximale d'un pentagone inscrit, nous devons trouver la longueur du côté qui maximise le produit des longueurs des côtés. Comme le pentagone est inscrit dans un cercle de rayon 5, la longueur du côté est donnée par \(s =2R sin(\frac{180^\circ}{5} ) = 2 \cdot 5sin(36^\circ )= 6.472 \) . Par conséquent, l'aire maximale d'un pentagone inscrit est obtenue lorsque le pentagone est régulier, et est donnée par:
\( A_\text{inscrit} = \frac{5s^2}{4} \cdot tan(36^\circ ) \approx 61.937\)

Pour trouver l'aire maximale d'un pentagone circonscrit, nous pouvons utiliser la formule du produit des côtés d'un polygone. Pour un pentagone, nous avons:
\( \small A_\text{circonscrit} =\frac{5s^2}{4} \cdot cot(36^\circ )=5R^2 sin(72^\circ ) \approx 78.589\)

Encore une fois, l'aire maximale d'un pentagone circonscrit est obtenue lorsque le pentagone est régulier.

En résumé, les polygones inscrits et circonscrits sont des concepts importants en géométrie qui impliquent des polygones inscrits à l'intérieur et circonscrits autour d'un cercle. Ces concepts ont de nombreuses propriétés intéressantes et sont utilisés dans divers domaines des mathématiques.

Cercles dessinés à l'intérieur et à l'extérieur d'un triangle ☰

Le sujet des cercles dessinés à l'intérieur et à l'extérieur d'un triangle est un aspect important de la géométrie élémentaire. Il existe divers théorèmes liés aux cercles dessinés à l'intérieur et à l'extérieur d'un triangle, qui sont discutés ci-dessous:

Cercle inscrit et centre du cercle inscrit:
Un cercle inscrit dans un triangle est un cercle tangent à chacun des trois côtés du triangle. Le centre du cercle inscrit est appelé le centre du cercle inscrit du triangle. Le centre du cercle inscrit est à égale distance de tous les trois côtés du triangle.

Théorème 1: Le centre du cercle inscrit d'un triangle est l'intersection de ses trois bissectrices d'angles.

Démonstration: Soit ABC un triangle, et soit I le centre de son cercle inscrit. Soient D, E et F les points où le cercle inscrit est tangent aux côtés BC, AC et AB, respectivement. Alors, ID, IE et IF sont les bissectrices perpendiculaires de EF, FD et DE, respectivement. Par conséquent, ID est la bissectrice de l'angle BIC, où B et C sont les sommets du triangle, et I est le centre du cercle inscrit. De même, IE et IF sont les bissectrices des angles AIC et AIB, respectivement. Par conséquent, les trois bissectrices d'angles du triangle se croisent au centre du cercle inscrit I.

Théorème 2: La distance du centre du cercle inscrit d'un triangle à l'un de ses côtés est égale au rayon du cercle inscrit.

Démonstration: Soit ABC un triangle, et soit I le centre de son cercle inscrit. Soient D, E et F les points où le cercle inscrit est tangent aux côtés BC, AC et AB, respectivement. Alors, ID, IE et IF sont les bissectrices perpendiculaires de EF, FD et DE, respectivement. Par conséquent, ID est la hauteur du triangle IBC du sommet I au côté BC. De même, IE et IF sont les hauteurs des triangles AIC et AIB du sommet I aux côtés AC et AB, respectivement. Comme \(ID=IE=IF\), il en découle que la distance du centre I du cercle inscrit à l'un des côtés du triangle est égale au rayon du cercle inscrit.

Cercle circonscrit et centre du cercle circonscrit:
Un cercle circonscrit à un triangle est un cercle qui passe par les trois sommets du triangle. Le centre du cercle circonscrit est appelé le centre du cercle circonscrit du triangle. Le centre du cercle circonscrit est l'intersection des bissectrices perpendiculaires des côtés du triangle.

Théorème 3: Le centre du cercle circonscrit d'un triangle est l'intersection des bissectrices perpendiculaires de ses côtés.

Démonstration: Soit ABC un triangle, et soit O le centre de son cercle circonscrit. Soient D, E et F les milieux des côtés BC, AC et AB, respectivement. Alors, OD, OE et OF sont les bissectrices perpendiculaires des côtés BC, AC et AB, respectivement. Par conséquent, OD est perpendiculaire à BC, et \(OD=\frac{1}{2} BC\). De même, OE est perpendiculaire à AC, et \(OE=\frac{1}{2} AC\). De même, OF est perpendiculaire à AB, et \( OF= \frac{1}{2} AB \). Par conséquent, O est à égale distance de tous les trois sommets du triangle et se trouve donc sur les bissectrices perpendiculaires de tous les trois côtés. Par conséquent, le centre du cercle circonscrit du triangle est l'intersection des bissectrices perpendiculaires de ses côtés.

Théorème 4: Les bissectrices perpendiculaires des côtés d'un triangle sont concourantes si et seulement si le triangle est aigu, droit ou obtus.

Démonstration : Soit ABC un triangle, et soit D, E et F les milieux des côtés BC, AC et AB, respectivement. Supposons que les bissectrices perpendiculaires des côtés BC, AC et AB sont concourantes en un point O. Alors, \(OD=OE=OF\), et donc O est à égale distance de tous les trois sommets du triangle. Par conséquent, \(OA=OB=OC\), et O est le centre du cercle circonscrit du triangle. Si le triangle est aigu, alors le centre du cercle circonscrit se trouve à l'intérieur du triangle. Si le triangle est droit, alors le centre du cercle circonscrit se trouve sur le milieu de l'hypoténuse. Si le triangle est obtus, alors le centre du cercle circonscrit se trouve à l'extérieur du triangle.

Réciproquement, supposons que le triangle soit aigu, droit ou obtus. Si le triangle est aigu, alors les bissectrices perpendiculaires des côtés se croisent à l'intérieur du triangle. Si le triangle est droit, alors les bissectrices perpendiculaires des côtés se croisent au milieu de l'hypoténuse. Si le triangle est obtus, alors les bissectrices perpendiculaires des côtés se croisent à l'extérieur du triangle. Par conséquent, les bissectrices perpendiculaires des côtés sont concourantes si et seulement si le triangle est aigu, droit ou obtus.

Cercles exinscrits et centres des cercles exinscrits:
Un cercle exinscrit d'un triangle est un cercle tangent à un côté du triangle et aux prolongements des deux autres côtés. Il existe trois cercles exinscrits d'un triangle, un pour chaque côté. Le centre d'un cercle exinscrit est appelé l'excentre du triangle correspondant à ce côté. L'excentre se trouve sur la bissectrice de l'angle extérieur au sommet opposé au côté tangent au cercle exinscrit.

Théorème 5: L'excentre d'un triangle correspondant à un côté donné se trouve sur la bissectrice de l'angle extérieur au sommet opposé à ce côté.

Démonstration: Soit ABC un triangle, et soit \(I_A\) le centre du cercle exinscrit correspondant au côté BC. Soit D le point de tangence du cercle exinscrit avec le côté BC, et soient E et F les points de tangence avec les côtés CA et AB, respectivement. Alors, \(I_A D\) est perpendiculaire à BC, et \(I_A E\) et \(I_A F\) sont les bissectrices des angles BAC et CAB, respectivement. Par conséquent, \(I_A\) se trouve sur la bissectrice de l'angle extérieur au sommet A. De même, l'excentre \(I_B\) correspondant au côté AC se trouve sur la bissectrice de l'angle extérieur au sommet B, et l'excentre \(I_C\) correspondant au côté AB se trouve sur la bissectrice de l'angle extérieur au sommet C.

En conclusion, le sujet des cercles dessinés à l'intérieur et à l'extérieur d'un triangle est un aspect important de la géométrie élémentaire. Les théorèmes liés aux cercles inscrits, circonscrits et exinscrits sont des résultats fondamentaux qui fournissent des informations précieuses sur les propriétés des triangles.

Propriétés d'un quadrilatère inscrit dans et circonscrit autour d'un cercle ☰

Un quadrilatère est dit inscrit dans un cercle si tous ses sommets se trouvent sur le cercle. De même, un quadrilatère est dit circonscrit autour d'un cercle si le cercle est tangent à tous ses côtés.

Propriétés d'un Quadrilatère Inscrit dans un Cercle:

• Les angles opposés d'un quadrilatère inscrit dans un cercle sont supplémentaires. Autrement dit, la somme des mesures de deux angles opposés est de 180 degrés.
• Les diagonales d'un quadrilatère inscrit dans un cercle se croisent à angle droit. Autrement dit, les diagonales sont perpendiculaires entre elles.
• Le produit des longueurs des deux diagonales d'un quadrilatère inscrit dans un cercle est égal à la somme des produits des longueurs des paires de côtés opposés. Autrement dit, si \(ABCD\) est un quadrilatère inscrit dans un cercle, alors \(AC \cdot BD=AB \cdot CD+AD \cdot BC\).
• Les segments de droite joignant les milieux des côtés opposés d'un quadrilatère inscrit dans un cercle sont concourants. Autrement dit, les segments AC et BD se rencontrent en un point P, où P est le milieu de EF et EF est le segment de droite joignant les milieux de AB et CD.

Propriétés d'un Quadrilatère Circonscrit autour d'un Cercle:

• Les côtés opposés d'un quadrilatère circonscrit autour d'un cercle sont parallèles. Autrement dit,
  \(AB \parallel CD\) et \( AD \parallel BC\).
• La somme des paires opposées de côtés d'un quadrilatère circonscrit autour d'un cercle est égale au diamètre du cercle. Autrement dit, \(AB+CD=AD+BC\).
• Les segments de droite joignant les points de contact du cercle avec les côtés d'un quadrilatère circonscrit autour d'un cercle sont concourants. Autrement dit, les segments AC et BD se rencontrent en un point P, où P est l'intersection des tangentes au cercle en B et D.
• La superficie d'un quadrilatère circonscrit autour d'un cercle peut être calculée en utilisant la formule de Brahmagupta:
  \( \text{Area} =\sqrt{(s-a)(s-b)(s-c)(s-d)} \), où \(a\), \(b\), \(c\) et \(d\) sont les longueurs des côtés du quadrilatère et \(s\) est le demi-périmètre, donné par: \(s=\frac{a+b+c+d}{2} \).
• Si un quadrilatère est à la fois inscrit dans et circonscrit autour d'un cercle, alors il doit être un carré. En d'autres termes, si un quadrilatère a la propriété que ses sommets se trouvent sur un cercle et que le cercle est tangent à tous ses côtés, alors le quadrilatère doit être un carré.

Cercles à l'intérieur et à l'extérieur d'un polygone régulier ☰

Un polygone régulier est un polygone dont tous les côtés et les angles sont égaux. Des cercles peuvent être inscrits à l'intérieur et circonscrits autour d'un polygone régulier.

Cercle inscrit dans un polygone régulier:
Un cercle inscrit dans un polygone régulier touche chaque côté du polygone en un seul point. Le centre du cercle est également le centre du polygone.
Soit \(r\) le rayon du cercle inscrit, \(s\) la longueur d'un côté du polygone régulier et \(n\) le nombre de côtés du polygone.
L'aire \(A\) du polygone régulier peut être calculée à l'aide de la formule: \( A=\frac{1}{2} nr^2 \sin \frac{2 \pi }{n} \).

Le périmètre \(P\) du polygone régulier est donné par: \(P=ns\).
Le rayon \(r\) du cercle inscrit peut être calculé à l'aide de la formule: \( r= \frac{s}{2 \tan \frac{\pi}{n}} \)

Cercle circonscrit autour d'un polygone régulier:
Un cercle circonscrit autour d'un polygone régulier passe par chaque sommet du polygone. Le centre du cercle est également le centre du polygone.
Soit \(R\) le rayon du cercle circonscrit, \(s\) la longueur d'un côté du polygone régulier et \(n\) le nombre de côtés du polygone.
L'aire \(A\) du polygone régulier peut être calculée à l'aide de la formule: \( A=\frac{1}{2} nR^2 \sin \frac{2 \pi }{n} \).

Le périmètre \(P\) du polygone régulier est donné par: \(P = ns\).
Le rayon \(R\) du cercle circonscrit peut être calculé à l'aide de la formule: \( R= \frac{s}{2 \sin \frac{\pi}{n}} \)

De plus, le rapport de l'aire du cercle circonscrit à l'aire du cercle inscrit est donné par:
\( \frac{\text{Aire du cercle circonscrit}}{ \text{Aire du cercle inscrit}} = \frac{R^2}{r^2} = \frac{\sin^2 \frac{\pi}{n}}{1- \sin^2 \frac{\pi}{n}} \)

Aire d'un polygone. Aire du polygone régulier. ☰

L'aire d'un polygone est la mesure de la région bidimensionnelle enclose par le polygone. La formule pour trouver l'aire d'un polygone dépend du type de polygone.
Par exemple, l'aire d'un triangle peut être calculée en utilisant la formule:
\( \text{Aire du triangle} = \frac{1}{2} \cdot \text{base} \cdot \text{hauteur} \)

Pour un rectangle, l'aire peut être calculée en utilisant la formule:
\( \text{Aire du rectangle} = \text{longueur} \cdot \text{largeur} \)

Pour les polygones irréguliers, il existe différentes méthodes pour calculer l'aire, telles que la diviser en formes plus simples et additionner les aires ou utiliser le calcul intégral.

En revanche, l'aire d'un polygone régulier peut être calculée en utilisant la formule suivante:
\( \small \text{Aire du polygone régulier} = \frac{1}{2} \cdot \text{Périmètre} \cdot \text{Apotème} \). Où le Périmètre est la somme des longueurs de tous les côtés du polygone, et l'Apotème est la distance perpendiculaire du centre du polygone à l'un de ses côtés.

Le polygone régulier est un polygone dont tous les côtés ont la même longueur et tous les angles ont la même mesure. Les exemples de polygones réguliers incluent les triangles équilatéraux, les carrés, les pentagones réguliers, les hexagones, etc.