Équations quadratiques ☰

La forme générale d'une équation quadratique est:
\(ax^2+bx+c=0\) , où \(a≠0\), \(a\), \(b\) et \(c\) sont des constantes et \(x\) est la variable.
L'équation quadratique peut être résolue en utilisant la formule quadratique, qui est:
\(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}\)
La formule quadratique fournit les solutions de l'équation quadratique, qui peuvent être réelles ou complexes, en fonction du discriminant \((b^2–4ac)\). Si le discriminant est positif, l'équation quadratique a deux racines réelles distinctes. Si le discriminant est nul, l'équation quadratique a une racine réelle, qui est une double racine. Si le discriminant est négatif, l'équation quadratique a deux racines complexes.

Équations quadratiques incomplètes:

Si au moins l'un des coefficients de \(b\) et \(c\) dans l'équation quadratique \(ax^2+bx+c=0\) est égal à zéro, alors l'équation est appelée une équation quadratique incomplète.

Résolution des équations quadratiques ☰

Il existe plusieurs méthodes pour résoudre les équations quadratiques, notamment:

• Factorisation: Cela consiste à écrire l'expression quadratique comme un produit de deux binômes et à établir chaque binôme égal à zéro pour trouver les racines de l'équation.
• Complétion du carré: Cela consiste à manipuler l'expression quadratique dans la forme d'un trinôme carré parfait, puis à résoudre pour les racines en utilisant l'algèbre de base.
• Formule quadratique: Cette formule donne les racines de n'importe quelle équation quadratique en fonction de ses coefficients, et peut être dérivée en utilisant la méthode de complétion du carré.
• Graphiques: Cela consiste à tracer la fonction quadratique et à identifier les \(x\)-interceptes, qui correspondent aux racines de l'équation.
• Méthodes numériques: Il existe plusieurs méthodes numériques qui peuvent être utilisées pour approximer les racines d'une équation quadratique, telles que la méthode de Newton, la méthode de la bissection et la méthode de la sécante.

Chacune de ces méthodes a ses avantages et ses inconvénients, et le choix de la méthode dépend du problème spécifique à résoudre et des outils et ressources disponibles.


Méthode de factorisation des équations quadratiques:
La méthode de factorisation est une technique utilisée pour factoriser les expressions quadratiques et résoudre les équations quadratiques. Pour factoriser une expression quadratique en utilisant cette méthode, nous devons trouver deux binômes qui se multiplient pour donner l'expression quadratique. La forme générale d'une expression quadratique est:
\(ax^2+bx+c\)

Pour factoriser cette expression quadratique, nous pouvons chercher deux binômes de la forme:
\((mx+r)(nx+s)\), où \(m\), \(n\), \(r\) et \(s\) sont des constantes. En développant le produit de ces deux binômes, nous obtenons:
\(mnx^2+(ms+rn)x+rs\).
En comparant cela à la forme générale de l'expression quadratique, nous pouvons voir que:
\(mn=a\)
\(ms+rn=b\)
\(rs=c\)

Nous pouvons utiliser ces équations pour résoudre \(m, n, r\) et \(s\). Une fois que nous avons trouvé ces constantes, nous pouvons écrire l'expression quadratique sous la forme factorisée:
\(ax^2+bx+c=(mx+r)(nx+s)\).
Pour résoudre une équation quadratique en utilisant la méthode de factorisation, nous pouvons d'abord factoriser l'expression quadratique comme indiqué ci-dessus. Une fois que nous avons factorisé l'expression quadratique, nous pouvons utiliser la propriété du produit nul pour trouver les racines de l'équation. La propriété du produit nul stipule que si le produit de deux facteurs est nul, alors au moins l'un des facteurs doit être nul. Par conséquent, si nous avons factorisé l'expression quadratique comme:
\((mx+r)(nx+s)=0\), alors nous pouvons mettre chaque facteur égal à zéro et résoudre pour \(x\):
\((mx+r)=0 \) ou \((nx+s) =0\)
En résolvant chaque équation linéaire, nous obtenons:
\(x=-\frac{r}{m}\) ou \(x=-\frac{s}{n}\)
Par conséquent, les racines de l'équation quadratique sont \(x=-\frac{r}{m}\) ou \(x=-\frac{s}{n}\).
Il convient de noter que toutes les expressions quadratiques ne peuvent pas être factorisées à l'aide de nombres réels. Dans ce cas, nous pouvons avoir besoin d'utiliser d'autres méthodes telles que la complétion du carré ou la formule quadratique pour trouver les racines de l'équation.

Exemple:
Supposons que nous ayons l'équation quadratique: \(x^2-5x+6=0\).
Pour résoudre cette équation en utilisant la méthode de factorisation, nous devons factoriser l'expression quadratique \( x^2–5x+6 \) en un produit de deux binômes. Nous pouvons chercher deux binômes de la forme:
\((mx+r)(nx+s)\), où \(m\), \(n\), \(r\) et \(s\) sont des constantes. En développant le produit de ces deux binômes, nous obtenons:
\(mnx^2+(ms+rn)x+rs\).
En comparant cela à l'expression quadratique \( x^2 –5x+6 \), nous pouvons voir que:
\(mn=1 \)
\(ms+rn=-5 \)
\(rs=6 \)
Nous pouvons essayer différentes valeurs de \(m\), \(n\), \(r\) et \(s\) jusqu'à ce que nous trouvions des valeurs qui satisfont ces équations.
Un ensemble possible de valeurs est \(m=1\), \(n=1\), \(r=-2\) et \(s=-3\) ce qui donne:
\((mx+r)(nx+s) \)
\((x-2)(x-3)=0 \)
Par conséquent, les racines de l'équation quadratique sont \(x=2\) et \(x=3\)
Nous pouvons vérifier que ces valeurs sont effectivement des racines de l'équation quadratique en les substituant dans l'équation d'origine
\(2^2-5\cdot 2+6=0 \)
\(3^2-5\cdot 3+6=0 \)
Les deux équations sont vraies, donc \(x=2\) et \(x=3\) sont effectivement des racines de l'équation quadratique.


Complétion du carré:
Nous devons d'abord écrire l'expression quadratique sous la forme d'un carré complet. Un carré complet est une expression de la forme \((x+a)^2=x^2+2ax+a^2\) , où \(a\) est une constante. Toute expression quadratique peut être écrite sous la forme d'un carré complet en ajoutant ou en soustrayant une constante.
Supposons que nous ayons une équation quadratique de la forme: \(ax^2+bx+c=0\)
Pour résoudre cette équation en divisant un carré complet, nous écrivons d'abord l'expression quadratique sous la forme d'un carré complet en ajoutant ou en soustrayant une constante. Nous pouvons le faire en complétant le carré comme suit:

\( a(x^2 + \frac{b}{a}x) = -c \)

\(a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) = -c + a(\frac{b^2}{4a^2})\)

\(a\left(x + \frac{b}{2a}\right)^2 = \frac{4ac - b^2}{4a}\)

Nous pouvons maintenant résoudre pour \(x\) en divisant les deux côtés par le coefficient du terme carré:

\((x + \frac{b}{2a})^2 = \frac{4ac - b^2}{4a^2}\)

\(x + \frac{b}{2a} = \sqrt{\frac{4ac - b^2}{4a^2}}\)

\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

C'est la formule quadratique, qui donne les racines de n'importe quelle équation quadratique de la forme \( ax^2 + bx + c = 0 \)
Nous pouvons également utiliser la formule quadratique pour vérifier si une expression quadratique Si le discriminant \( b^2 –4ac \) est un carré parfait, alors l'expression quadratique peut être écrite sous la forme d'un carré complet. Si le discriminant n'est pas un carré parfait, alors l'expression quadratique ne peut pas être écrite sous la forme d'un carré complet.

Exemple:
Prenons l'équation quadratique: \(x^2+6x+1=0\).
Pour compléter le carré, nous voulons réécrire l'équation sous la forme de \((x+a)^2+b\), où \(a\) et \(b\) sont des constantes.
Tout d'abord, nous ajouterons et soustrairons \((\frac{b}{2})^2\) \( ( (\frac{6}{2})^2 =9 ) \) au côté gauche de l'équation pour obtenir:
\(x^2+6x+9-9+1=0\)
Remarquez que les trois premiers termes du côté gauche forment un trinôme carré parfait, que nous pouvons écrire sous la forme \((x+3)^2\)
Nous pouvons donc réécrire l'équation comme suit: \((x+3)^2-8=0\)
Maintenant, nous pouvons résoudre pour \(x\) en ajoutant 8 des deux côtés et en prenant la racine carrée:
\((x+3)^2=8 \)
\(x+3=\pm \sqrt{8} \)
\(x=-3 \pm \sqrt{8} \)
Les solutions de l'équation d'origine sont donc:
\(x=-3+ \sqrt{8} \) et \(x=-3- \sqrt{8} \)
Et voilà comment compléter le carré d'une équation quadratique !


Graphiques:
Les graphiques sont une méthode visuelle pour résoudre les équations quadratiques. L'idée derrière cette méthode est de tracer l'équation quadratique et d'identifier les \(x\)-interceptes, qui correspondent aux solutions de l'équation.
Əgər \(a > 0\) olarsa, parabola yuxarıya, \(a < 0\) olarsa, aşağıya doğru açılır.
Pour tracer une équation quadratique, nous la réécrivons d'abord sous la forme \( y=ax^2 +bx+c \), où \(y\) est la variable dépendante et \(x\) est la variable indépendante. Le graphique d'une équation quadratique est une parabole, qui est une courbe en forme de U. La direction et la forme de la parabole dépendent du signe du coefficient \(a\). Si \( a > 0 \), la parabole s'ouvre vers le haut, et si \( a < 0 \), la parabole s'ouvre vers le bas.
Pour trouver les \(x\)-interceptes de la parabole, nous fixons \(y=0\) et résolvons pour \(x\). Cela nous donne les valeurs de \(x\) où la parabole intersecte l'axe \(x\). Ces valeurs correspondent aux solutions de l'équation quadratique.

Prenons un exemple pour illustrer cette méthode. Supposons que nous voulions résoudre l'équation quadratique: \(x^2-4x-5=0\).
Nous pouvons réécrire cette équation sous la forme \( y=x^2 –4x-5 \) Pour tracer la parabole, nous pouvons utiliser une calculatrice graphique ou un programme logiciel, ou nous pouvons le dessiner à la main.

Graphique:


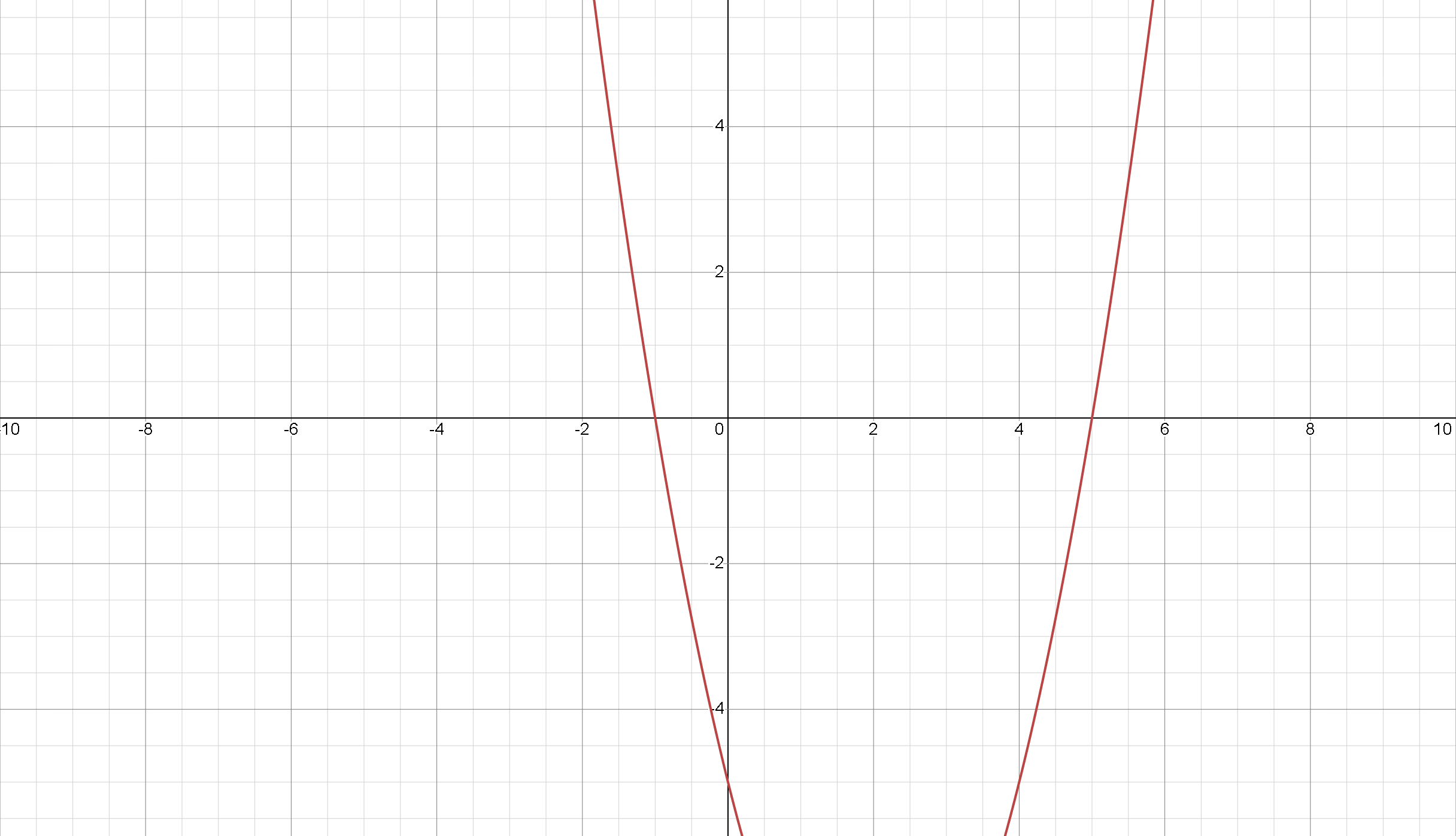
Nous pouvons voir que la parabole intersecte l'axe \(x\) à deux points, qui correspondent aux solutions de l'équation. Pour trouver ces points, nous pouvons soit utiliser la formule quadratique, soit estimer les valeurs de \(x\) à partir du graphique. Dans ce cas, les \(x\)-interceptes sont approximativement \(x=-1\) et \(x=5\), qui sont les solutions de l'équation quadratique.

En résumé, le graphique est une méthode utile pour résoudre les équations quadratiques visuellement. En traçant l'équation et en identifiant les \(x\)-interceptes, nous pouvons rapidement trouver les solutions de l'équation.

Formule quadratique ☰

La formule pour les racines d'une équation quadratique de la forme \(ax^2+bx+c=0\) est appelée la formule quadratique. Elle est donnée par:

\(x =\frac{-b \pm \sqrt{b^2- 4ac}}{2a}\)

Cette formule nous donne les valeurs de \(x\), qui sont les racines ou solutions de l'équation quadratique. Le symbole \( \pm \) signifie que nous devons trouver à la fois les racines positives et négatives. L'expression à l'intérieur de la racine carrée, \( (b^2 – 4ac) \), est appelée le discriminant de l'équation quadratique, et elle nous indique combien de racines réelles l'équation a.

Si le discriminant est positif \( (b^2 –4ac > 0) \), l'équation quadratique a deux racines réelles distinctes, données par la formule ci-dessus.

Si le discriminant est nul \( (b^2 –4ac=0) \), l'équation quadratique a une racine réelle, qui est donnée par \(x=-\frac{b}{2a}\)

Si le discriminant est négatif \( (b^2 – 4ac < 0) \), l'équation quadratique a deux racines complexes, qui sont données par:

\(x =\frac{-b \pm i\sqrt{4ac-b^2}}{2a}\) ,

où \(i\) est l'unité imaginaire, égale à la racine carrée de \(-1\).
La formule quadratique est un outil puissant pour résoudre les équations quadratiques, et elle peut être utilisée pour n'importe quelle équation quadratique, quelle que soit les valeurs des coefficients \(a\), \(b\) et \(c\).

Théorème de Viète ☰

Le théorème de Viète, également connu sous le nom de formules de Viète ou relations de Viète, est un théorème fondamental en algèbre qui relie les coefficients d'un polynôme aux sommes et produits de ses racines. Le théorème est nommé d'après le mathématicien français François Viète (latinisé en Franciscus Vieta), qui l'a découvert pour la première fois au 16ème siècle.

Plus précisément, le théorème de Viète énonce que pour un polynôme de degré \(n\) avec des coefficients \(a_n,a_{n-1},…,a_1,a_0\) et des racines \(r_1,r_2,…,r_n\), les relations suivantes tiennent: La somme des racines est égale au ratio du coefficient opposé et du coefficient principal:
\(r_1+r_2+…+r_n=-\frac{a_{n-1}}{a_n}\)

La somme des produits des racines prises deux par deux est égale au ratio du terme constant et du coefficient principal avec un changement de signe selon la parité de \(n\): $$ r_1 r_2+r_1 r_3+…+r_{n-1}r_n=(-1)^n \cdot \frac{a_0}{a_n} $$

La somme des produits des racines prises trois par trois est égale au ratio du coefficient du terme au deuxième rang et du coefficient principal avec un changement de signe selon la parité de \(n\): $$ r_1 r_2 r_3+r_1 r_2 r_4+…+r_{n-2} r_{n-1} r_n=(-1)^{n-1} \cdot \frac{a_{n-2}}{a_n} $$

et ainsi de suite, avec la somme des produits des racines prises \(k\) par \(k\) étant égale à
\( (-1)^{n-k} \cdot \frac{a_{n-k}}{a_n} \) pour \( k = 1,2,…,n \).

Ces relations sont utiles pour résoudre des équations impliquant des racines de polynômes, car elles permettent d'exprimer les coefficients d'un polynôme en fonction de ses racines et vice versa.

Le théorème de Viète peut être appliqué aux équations quadratiques, qui sont des polynômes de degré 2. Pour une équation quadratique de la forme \(ax^2+bx+c=0\), les racines peuvent être trouvées en utilisant la formule quadratique:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)

En utilisant le théorème de Viète, nous pouvons relier les racines de l'équation quadratique à ses coefficients comme suit:

La somme des racines est égale à l'opposé du coefficient de \(x\) divisé par le coefficient de \(x^2\):
\( r1+r2=- \frac{b}{a} \)

Le produit des racines est égal au terme constant divisé par le coefficient de \(𝑥^2\):
\( 𝑟1 \cdot 𝑟2= \frac{c}{a} \)

Ces relations peuvent être dérivées en développant l'équation quadratique en utilisant la propriété distributive et en comparant l'expression résultante à la forme standard d'une équation quadratique.

Par exemple, supposons que nous ayons l'équation quadratique \( x^2+5x+6=0 \). En utilisant la formule quadratique, nous pouvons trouver les racines pour être -2 et -3. En utilisant le théorème de Viète, nous pouvons vérifier que ces valeurs satisfont les relations:
\( -2+(-3)= -\frac{5}{1} \) qui est l'opposé du coefficient de \(x\) (5) divisé par le coefficient de \(x^2\) (1).
\( -2 \cdot (-3)= \frac{6}{1} \) , qui est le terme constant (6) divisé par le coefficient de \( x^2 \) (1).

Ces relations sont valables pour toutes les équations quadratiques et sont utiles pour résoudre les problèmes qui impliquent de trouver les racines d'une équation quadratique ou d'exprimer les coefficients d'une équation quadratique en fonction de ses racines.

Les équations quadratiques peuvent être utilisées pour résoudre une large gamme de problèmes dans divers domaines, tels que la physique, l'ingénierie, la finance, et plus encore. Voici quelques exemples de résolution de problèmes à l'aide d'équations quadratiques:

• Mouvement de projectile: Un projectile lancé depuis le sol avec une vitesse initiale \(v0\) et un angle \(\theta \) suit une trajectoire parabolique décrite par l'équation \( y = -\frac{1}{{2g\left(\frac{x}{v_0\cos\theta}\right)^2}} + x\tan\theta \), ici \(g\) est l'accélération due à la gravité. Cette équation peut être réécrite sous forme d'équation quadratique en \(x\), ce qui peut être utilisé pour déterminer la distance horizontale parcourue par le projectile, la hauteur maximale atteinte et le temps de vol.
• Optimisation quadratique: Dans de nombreux problèmes d'optimisation, la fonction objectif peut être exprimée sous forme d'équation quadratique, telle que \( f(x)=ax^2+bx+c \), où \(a > 0\). Pour trouver la valeur maximale ou minimale de la fonction, nous pouvons utiliser la formule du sommet, qui donne la coordonnée \(x\) du sommet comme \( -\frac{b}{2a} \) et la coordonnée \(y\) correspondante comme \(f ( -\frac{b}{2a} ) \)
• Entreprises et finances: En affaires et en finances, les équations quadratiques peuvent être utilisées pour modéliser diverses situations, telles que la maximisation des profits et des revenus, la minimisation des coûts et l'analyse du point mort. Par exemple, la fonction de profit pour un produit peut être exprimée comme \(P(x)=-ax^2+bx-c \), où \(x\) est le nombre d'unités vendues et \(a\), \(b\) et \(c\) sont des constantes. Pour trouver le niveau de production maximisant le profit, nous pouvons utiliser la formule quadratique pour déterminer la valeur de \(x\) qui maximise \(P(x)\)
• Ingénierie: En ingénierie, les équations quadratiques peuvent être utilisées pour modéliser et résoudre divers problèmes, tels que la détermination de la fréquence naturelle d'un système vibrant, la conception optimale d'une structure ou d'une machine, et la trajectoire d'un véhicule ou d'un missile. Par exemple, la fréquence naturelle d'un système vibrant peut être exprimée comme \( \omega = \sqrt{\frac{k}{m}}\) , où \(k\) est la constante de rappel et \(m\) est la masse du système. Cette équation peut être réarrangée pour donner une équation quadratique en \( \omega ^2 \), qui peut être résolue pour déterminer la fréquence naturelle.

Ce ne sont que quelques exemples de résolution de problèmes à l'aide d'équations quadratiques. En général, les équations quadratiques peuvent être utilisées pour modéliser et résoudre une large gamme de problèmes, et sont un outil puissant dans de nombreux domaines d'étude.