Inégalités quadratiques ☰

Une inégalité quadratique est un type d'inégalité dans laquelle une fonction quadratique apparaît. Les inégalités quadratiques ont la forme:
\( ax^2 + bx + c,,,,op,,,,0 \), où \(a\), \(b\) et \(c\) sont des nombres réels et \(op\) est l'un des symboles d'inégalité \( < \), \( \le \), \(> \) ou \( \ge \).

La solution à une inégalité quadratique est l'ensemble de toutes les valeurs de \(x\) qui satisfont l'inégalité. Pour trouver l'ensemble solution, nous pouvons utiliser les étapes suivantes:

• Résoudre l'équation quadratique correspondante \( ax^2 + bx + c = 0 \) pour trouver les racines de la fonction quadratique.
• Tracer le graphe de la fonction quadratique sur un plan cartésien.
• Déterminer la ou les régions du graphe qui se trouvent au-dessus ou en dessous de l'axe des \(x\), en fonction du signe de \(a\).
• Ombrer la ou les régions appropriées du graphe, en fonction du symbole d'inégalité.
• Écrire l'ensemble solution en utilisant la notation par intervalles ou la notation ensembliste.

Voyons quelques exemples:
Exemple 1: Résoudre l'inégalité \(x^2 - 4x + 3 \ge 0 \).
Solution: Tout d'abord, trouvons les racines de l'équation quadratique correspondante \(x^2 - 4x + 3 = 0 \) en factorisant ou en utilisant la formule quadratique:
\( x^2 - 4x + 3 = (x-1)(x-3)=0 \).
Ainsi, les racines sont \( x=1 \) et \(x=3 \).
Ensuite, nous traçons le graphe de la fonction quadratique \( f(x) = x^2 - 4x + 3 \).

Graphe


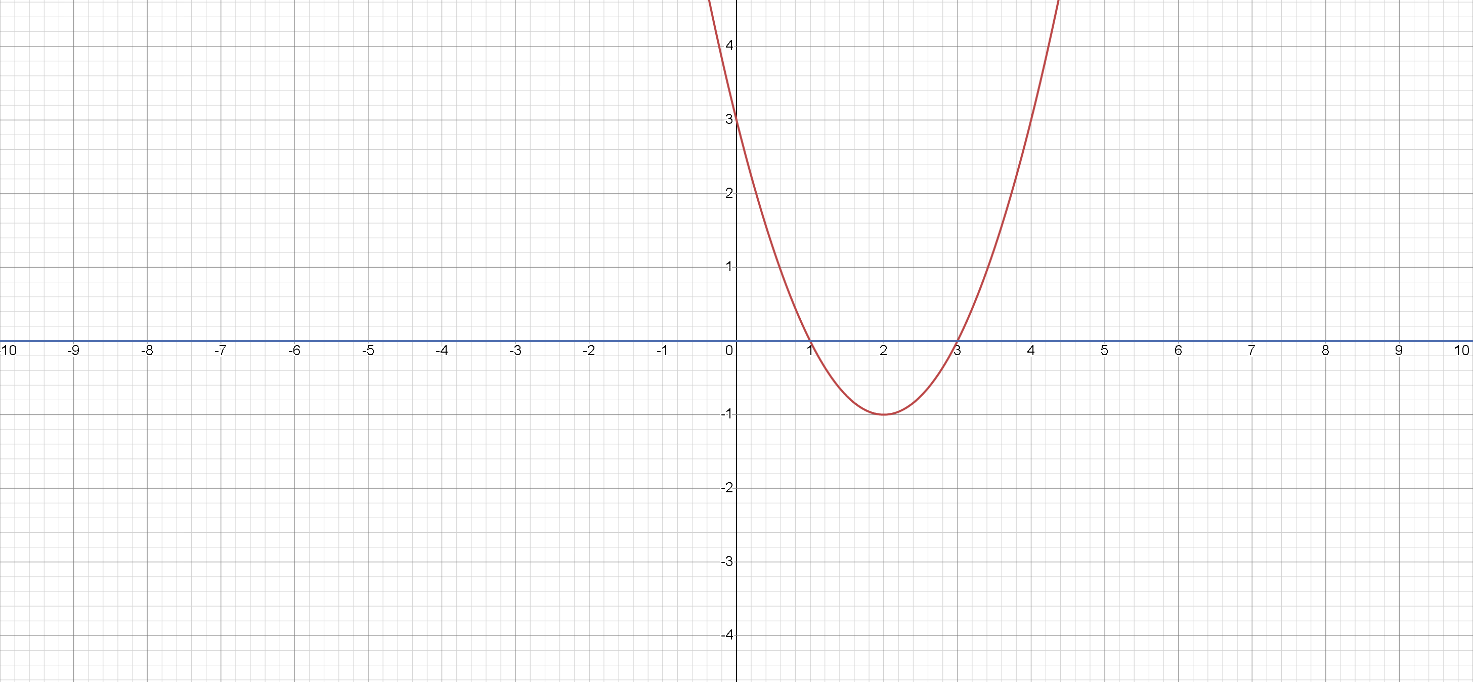
Nous pouvons voir que le graphe de la fonction est au-dessus de l'axe des \(x\) entre les racines \(x=1\) et \(x=3\).
Par conséquent, la solution de l'inégalité \( x^2 - 4x + 3 \ge 0 \) est : \( x \in (-\infty, 1] \cup [3, \infty) \).

Exemple 2: Un exemple de résolution d'une inégalité quadratique par la méthode des intervalles.
Considérons l'inégalité: \( 2x^2 - 5x - 3 < 0 \).
Pour résoudre cette inégalité, nous trouvons d'abord les racines de l'équation quadratique \( 2x^2–5x–3=0 \)
\( x=- \frac{1}{2} \) et \( x = 3 \). Nous pouvons trouver ces racines en factorisant le quadratique ou en utilisant la formule quadratique.
Ensuite, nous utilisons les racines pour diviser la droite numérique en trois intervalles:
\( (-\infty ; -\frac{1}{2} ) \), \( (-\frac{1}{2}; 3) \) et \( (3; \infty)\).
Ensuite, nous testons une valeur de chaque intervalle dans l'inégalité pour déterminer si elle est vraie ou fausse dans cet intervalle.

Pour l'intervalle \( (-\infty ; -\frac{1}{2}) \) nous pouvons choisir \( x= -1 \) comme valeur de test.
En substituant \(x=-1\) dans l'inégalité, nous obtenons: \( 2(-1)^2 - 5(-1) - 3 < 0 \), ce qui se simplifie en: \( 4 < 0 \).
C'est faux, donc l'inégalité ne tient pas dans l'intervalle \( (-\infty ; -\frac{1}{2}) \) .

Pour l'intervalle \( (-\frac{1}{2} ; 3) \) nous pouvons choisir \(x=0\) comme valeur de test.
En substituant \(x=0\) dans l'inégalité, nous obtenons: \( 2(0)^2 - 5(0) - 3 < 0 \), ce qui se simplifie en: \( -3 < 0 \).
C'est vrai, donc l'inégalité tient dans l'intervalle \( (-\frac{1}{2} ; 3) \).

Pour l'intervalle \( (3; \infty) \) nous pouvons choisir \(x=4\) comme valeur de test.
En substituant \(x=4\) dans l'inégalité, nous obtenons: \(2(4)^2 - 5(4) - 3 < 0 \), ce qui se simplifie en: \( 5 < 0 \) .
C'est faux, donc l'inégalité ne tient pas dans l'intervalle \( (3;\infty) \).

Par conséquent, la solution de l'inégalité \( 2x^2–5x–3 < 0 \) est: \( x\ \in (- \frac{1}{2} ; 3) \)
Cela signifie que toute valeur de \(x\) qui est supérieure à \(- \frac{1}{2} \) et inférieure à \(3\) rend l'inégalité vraie.

Résolution des inégalités rationnelles par la méthode des intervalles ☰

Pour résoudre des inégalités rationnelles par la méthode des intervalles, suivez ces étapes:

• Réécrivez l'inégalité sous forme d'une expression rationnelle unique, avec zéro d'un côté, et l'autre côté dans une seule fraction.
• Déterminez les valeurs critiques de l'expression en trouvant où le numérateur et le dénominateur sont égaux à zéro.
• Divisez la droite numérique en intervalles séparés par les valeurs critiques trouvées à l'étape 2.
• Déterminez le signe de l'expression dans chaque intervalle, et identifiez les intervalles où l'expression est positive ou négative.
• Écrivez la solution en notation d'intervalle, en utilisant les intervalles où l'expression est positive ou négative, en fonction de la direction de l'inégalité.

Par exemple, résolvons l'inégalité \(\frac{2x-5}{x+1} > 1 \) par la méthode des intervalles.
1. Réécrivez l'inégalité sous forme d'une expression rationnelle unique:
\(\frac{2x-5}{x+1} -1 > 0 \)

Simplifiez le côté gauche et combinez les termes semblables:
\( \frac{2x-5-(x+1)}{x+1} > 0 \)

\( \frac{x-6}{x+1} \)


2. Déterminez les valeurs critiques en fixant le numérateur et le dénominateur à zéro:
\( x-6=0 \rightarrow x=6 \).
\( x+1=0 \rightarrow x=-1 \).


3. Divisez la droite numérique en intervalles:
\( (-\infty ; -1) \), \( (-1;6) \), \( (6;\infty ) \).


4. Déterminez le signe de l'expression dans chaque intervalle en testant un point dans chaque intervalle:
Pour \( x=-2 \), \( \frac{-2-6}{-2+1} = 8 > 0 \) , donc l'expression est positive dans \( (-\infty ; -1) \).

Pour \( x = 0 \), \( \frac{0-6}{0+1} = -6 < 0 \) , donc l'expression est négative dans \( (-1 ; 6 ) \).

Pour \( x = 7 \), \( \frac{7-6}{7+1} = \frac{1}{8} > 0 \) , donc l'expression est positive dans \( (6; \infty ) \).


5. Écrivez la solution en notation d'intervalle:
L'inégalité est vraie là où l'expression est positive, donc la solution est \( x \in (- \infty ; -1 ) \cup (6; \infty ) \).

Inégalités irrationnelles ☰

Une inégalité irrationnelle est une inégalité impliquant une ou plusieurs expressions irrationnelles, telles que des racines carrées ou des racines cubiques. Le processus pour résoudre une inégalité irrationnelle est différent de celui pour résoudre une inégalité régulière, car le fait de mettre au carré ou de mettre à une puissance peut introduire des solutions erronées. Pour résoudre une inégalité irrationnelle, vous devez isoler l'expression irrationnelle d'un côté de l'inégalité, puis mettre au carré ou élever les deux côtés de l'inégalité pour éliminer le radical. Cependant, en faisant cela, vous pouvez introduire des solutions qui ne sont pas valides pour l'inégalité d'origine, car mettre au carré ou élever à une puissance peut changer le signe d'un nombre. Par conséquent, vous devez vérifier vos solutions pour vous assurer qu'elles sont valides pour l'inégalité d'origine.

Pour résoudre des inégalités irrationnelles, suivez ces étapes générales:
1. Isoler l'expression irrationnelle d'un côté de l'inégalité.

2. Mettre au carré les deux côtés de l'inégalité (ou élever les deux côtés à une puissance qui élimine le radical).

3. Résoudre l'inégalité résultante.

4. Vérifiez les solutions de l'inégalité d'origine, car mettre au carré ou élever à une puissance peut introduire des solutions erronées.


Par exemple, résolvons l'inégalité \( \sqrt{2x-1} > 3 \) .

1. Mettons les deux côtés de l'inégalité au carré:
\( (\sqrt{2x-1})^2 > 3^2 \rightarrow 2x - 1 > 9 \)

2. Résolvons l'inégalité résultante:
\( 2x > 10 \rightarrow x > 5 \) .
\( \small \sqrt{2x-1} > 3 \rightarrow 2x > 10 \rightarrow x > 5 \)

3. Vérifions la solution de l'inégalité d'origine:
Substituons \(x=6\) dans l'inégalité d'origine:
\( \sqrt{2(6)-1} > 3 \rightarrow \sqrt{11} > 3 \)
C'est vrai, donc \(x=6\) est une solution valide pour l'inégalité.

Substituons \(x=4\) dans l'inégalité d'origine:
\( \sqrt{2(4)-1} > 3 \rightarrow \sqrt{7} > 3 \)
C'est faux, donc \(x=4\) n'est pas une solution valide pour l'inégalité.
Par conséquent, la solution est \(x > 5\).

Remarque: Notez toujours que l'expression de la racine ne peut pas être un nombre négatif.