Fonctions périodiques. Périodicité des fonctions trigonométriques. ☰

Les fonctions périodiques sont des fonctions qui répètent leurs valeurs à intervalles réguliers ou périodes. Le concept de périodicité est important dans diverses branches des mathématiques, telles que l'analyse de Fourier et le traitement du signal. Une fonction \(f(x)\) est dite périodique s'il existe une constante non nulle \(P\) telle que pour tout \(x\) dans le domaine de \(f\), la condition suivante est vérifiée:
\(f(x+P)=f(x)\).

La plus petite valeur positive de \(P\) pour laquelle cette condition est satisfaite est appelée la période de la fonction.

Les fonctions trigonométriques, telles que le sinus et le cosinus, sont des exemples fondamentaux de fonctions périodiques. Parlons de la périodicité des fonctions sinus et cosinus:

Fonction sinus: La fonction sinus, notée \( \sin(x) \), est périodique avec une période de \( 2 \pi \). Cela signifie que pour tout \(x\):
\( \sin(x+2 \pi )=\sin(x) \).

En d'autres termes, la fonction sinus répète ses valeurs tous les \( 2 \pi \) unités le long de l'axe des \(x\).

Fonction cosinus: La fonction cosinus, notée \( \cos(x) \), est également périodique avec une période de \( 2 \pi \). Cela signifie que pour tout \(x\):
\( \cos(x+ 2 \pi )=\cos(x) \).

Comme la fonction sinus, la fonction cosinus répète également ses valeurs tous les \( 2 \pi \) unités le long de l'axe des \(x\).

La fonction tangente, notée \( \tan(x) \), est un autre exemple de fonction trigonométrique périodique. Cependant, sa période est différente des fonctions sinus et cosinus. La fonction tangente a une période de \( \pi \), ce qui signifie que pour tout \(x\):
\( \tan(x+ \pi )=\tan(x) \).

La fonction tangente répète ses valeurs tous les \( \pi\) unités le long de l'axe des \(x\).

En résumé, les fonctions trigonométriques sont des fonctions périodiques, avec les fonctions sinus et cosinus ayant une période de \( 2 \pi \), et la fonction tangente ayant une période de \( \pi \). Ces propriétés périodiques sont essentielles pour résoudre des équations trigonométriques et analyser des phénomènes périodiques dans diverses applications scientifiques et d'ingénierie.

Graphes des fonctions sinus (y=sin(x)) et cosinus (y=cos(x)) ☰

Les graphes des fonctions sinus et cosinus, \( y=\sin(x) \) et \(y=\cos(x) \), sont essentiels pour comprendre leurs propriétés et leur comportement. Les deux fonctions sont périodiques et oscillent entre \(-1\) et \(1\). Les graphes illustrent la périodicité et l'amplitude de ces fonctions. Explorons en détail les graphes des deux fonctions.

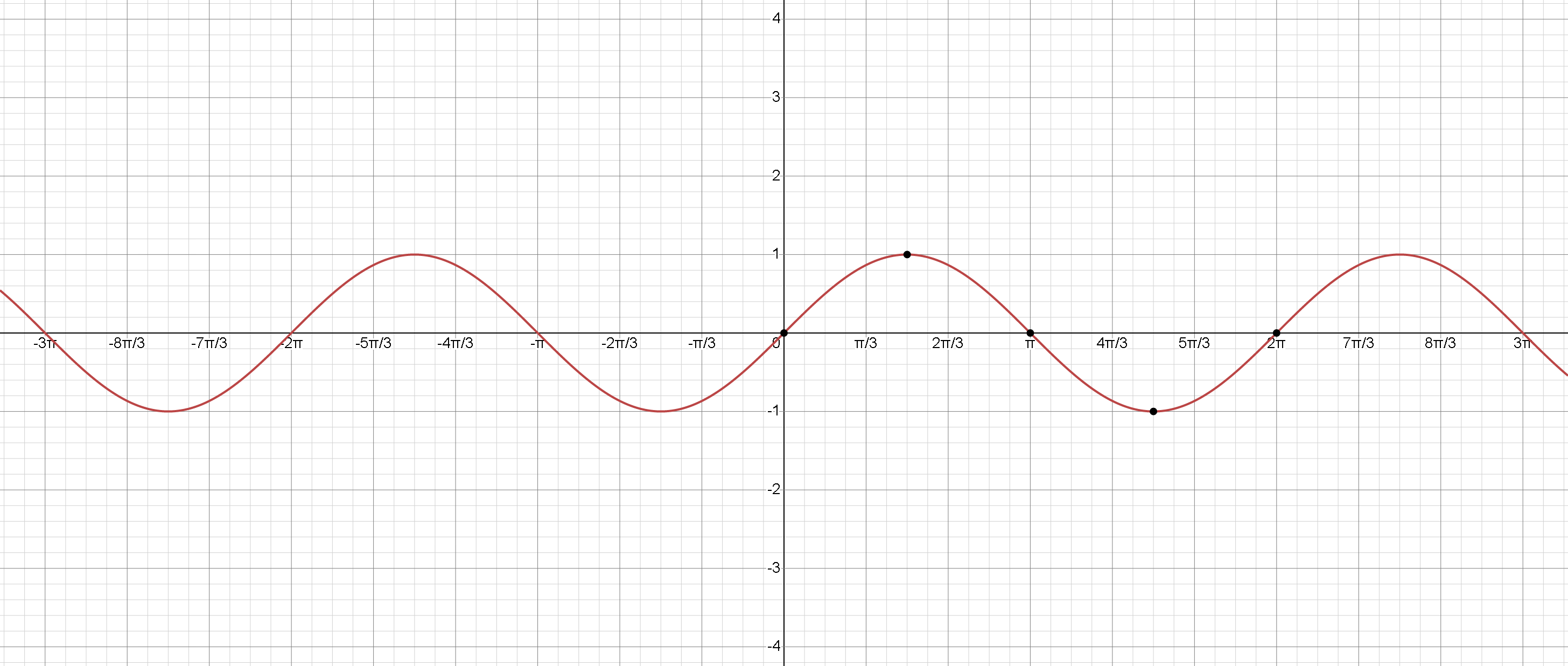
Graphique de \( y=\sin(x) \):
La fonction sinus a une période de \( 2 \pi \). Cela signifie qu'elle répète ses valeurs tous les \( 2 \pi \) unités le long de l'axe des \(x\). Le graphe de la fonction sinus démarre à l'origine \((0,0)\) et oscille entre \(-1\) et \(1\) avec quelques points clés:
\( x = \frac{ \pi }{2} \), \( \sin(x)=1 \) (valeur maximale)
\( x = \pi \), \( \sin(x) = 0 \) (passage par zéro)
\( x= \frac{3 \pi }{2} \), \( \sin(x)=-1 \) (valeur minimale)
\(x=2 \pi \), \( \sin(x)=0 \) (passage par zéro et un cycle complet)

La fonction sinus a une forme semblable à une onde, et son graphe est symétrique par rapport à l'origine (fonction impaire). Le graphe s'étend indéfiniment dans les directions positives et négatives de \(x\), répétant son motif tous les \(2 \pi \) unités.


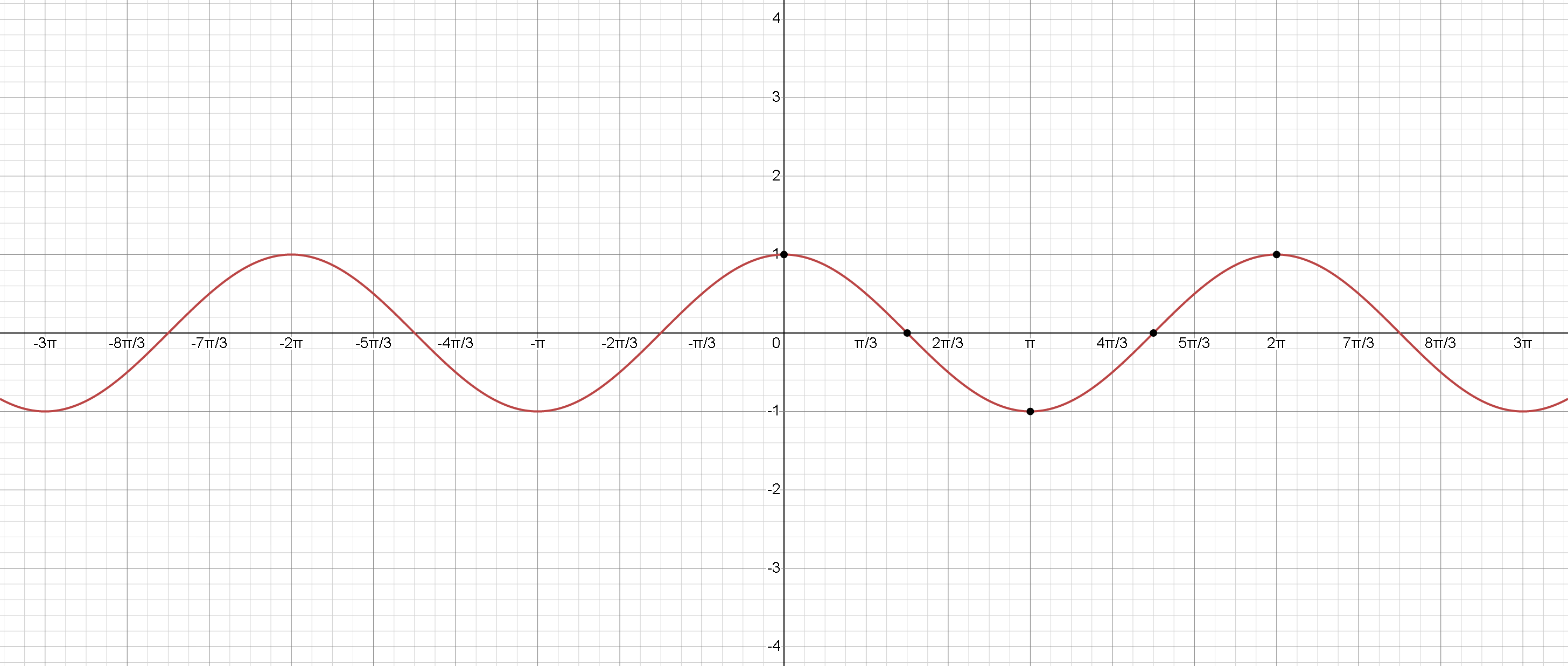
Graphique de \(y=\cos(x) \):
La fonction cosinus, tout comme la fonction sinus, a une période de \(2 \pi \) et oscille entre \(-1\) et \(1\). Cependant, le graphe de la fonction cosinus est déphasé de \( \frac{\pi}{2} \) unités vers la gauche par rapport à la fonction sinus. Voici quelques points clés pour la fonction cosinus:
\( x =0 \), \( \cos(x)=1 \) (valeur maximale)
\( x = \frac{ \pi }{2} \), \( \cos(x)=0 \) (passage par zéro)
\( x = \pi \), \( \cos(x)= -1 \) (valeur minimale)
\( x= \frac{3 \pi }{2} \), \( \cos(x)=0 \) (passage par zéro)
\(x = 2 \pi \), \( \cos(x)= 1\) (passage par zéro et un cycle complet)

La fonction cosinus a également une forme semblable à une onde, et son graphe est symétrique par rapport à l'axe des \(y\) (fonction paire). Le graphe s'étend indéfiniment dans les directions positives et négatives de \(x\), répétant son motif tous les \(2 \pi \) unités.

En résumé, les graphes des fonctions sinus et cosinus sont des motifs périodiques en forme d'onde qui oscillent entre \(-1\) et \(1\). Ils ont une période de \( 2 \pi \), la fonction cosinus étant déphasée de \( \frac{\pi }{2} \) unités vers la gauche par rapport à la fonction sinus. Ces graphiques aident à visualiser les propriétés et le comportement des fonctions sinus et cosinus, qui sont fondamentales en trigonométrie et dans diverses applications en mathématiques, sciences et ingénierie.

Transformations des fonctions sinus et cosinus☰

Les transformations des fonctions sinus et cosinus consistent à modifier les fonctions sinus et cosinus de base pour créer de nouvelles fonctions avec différentes propriétés, telles que l'amplitude, la période, le décalage de phase et le décalage vertical. Ces transformations nous permettent de modéliser un large éventail de phénomènes périodiques dans divers domaines, tels que la physique, l'ingénierie et la musique. Les fonctions sinus et cosinus de base sont données par:
\( f(x) = \sin(x) \)
\( g(x) = \cos(x) \)

Voici un bref aperçu des quatre transformations courantes:

• Amplitude: L'amplitude est la valeur maximale de la fonction, ou la distance maximale par rapport à l'axe central de la fonction. Modifier l'amplitude implique de multiplier la fonction sinus ou cosinus par une constante, notée "\(A\)":
  • \( f(x)= Asin(x) \)
  • \( g(x) = Acos(x) \)
  Si \( A > 1 \), l'amplitude augmente, et si \( 0 < A < 1 \), l'amplitude diminue. Si \(A\) est négatif, la fonction est réfléchie par rapport à l'axe horizontal.
• Période: La période est l'intervalle sur lequel la fonction se répète. Pour modifier la période de la fonction sinus ou cosinus, nous multiplions la variable d'entrée \((x)\) par une constante, notée "\(B\)":
  • \( f(x) = sin(Bx) \)
  • \( g(x) = cos(Bx) \)
  La nouvelle période de la fonction est obtenue en divisant la période originale (\( 2 \pi \) pour les fonctions sinus et cosinus) par la valeur absolue de \(B\):
  \( \text{Nouvelle période } = \frac{2 \pi }{ |B| } \). Si \( B > 1 \), la fonction est compressée horizontalement, et si \( 0 < B < 1 \), la fonction est étirée horizontalement.
• Décalage de phase: Le décalage de phase est un décalage horizontal de la fonction. Il est obtenu en ajoutant ou en soustrayant une constante, notée "\(C\)", à la variable d'entrée \((x)\):
  • \( f(x) = sin( B \cdot (x-C) ) \)
  • \( g(x) = cos ( B \cdot (x-C) ) \)
  Un décalage de phase positif \( (C > 0 ) \) déplace la fonction vers la droite, et un décalage de phase négatif \( (C < 0) \) déplace la fonction vers la gauche.
• Décalage vertical: Le décalage vertical déplace la fonction vers le haut ou vers le bas en ajoutant ou en soustrayant une constante, notée "\(D\)", à toute la fonction:
  • \( f(x) = Asin(B(x - C)) + D \)
  • \( g(x) = Acos(B(x - C)) + D \)
  Un décalage vertical positif \((D > 0) \) déplace la fonction vers le haut, et un décalage vertical négatif \( (D < 0) \) déplace la fonction vers le bas.

En résumé, les transformations des fonctions sinus et cosinus impliquent de modifier leur amplitude, leur période, leur décalage de phase et leur décalage vertical pour modéliser différents phénomènes périodiques. Les fonctions sinus et cosinus transformées générales peuvent être écrites comme suit:
\( f(x) = Asin(B(x-C))+D \)
\( g(x) = Acos(B(x-C))+D \)

Pour continuer à explorer les transformations des fonctions sinus et cosinus, examinons quelques exemples et applications de ces transformations.

• Exemple 1: Traitement du signal
  En traitement du signal, la modulation d'amplitude \((AM)\) est une technique utilisée pour transmettre des informations en variant l'amplitude d'un signal d'onde continue. La modulation peut être représentée par le produit de l'onde porteuse et du signal de message:
  \( y(t)= (A + Msin(Bmt)) \cdot cos(Bc\cdot t) \)
  
  Ici, \(A\) représente l'amplitude de l'onde porteuse, \(Bc\) est la fréquence angulaire de l'onde porteuse, \(M\) est l'amplitude du signal de message, \(Bm\) est la fréquence angulaire du signal de message, et \(t\) est la variable temporelle. La transformation permet de combiner une onde porteuse haute fréquence avec un signal de message basse fréquence.
• Exemple 2: Physique - Mouvement harmonique simple
  En physique, le mouvement harmonique simple \((SHM)\) décrit le mouvement d'un objet oscillant, tel qu'une masse attachée à un ressort ou un pendule. Le déplacement de l'objet par rapport à sa position d'équilibre en fonction du temps peut être modélisé à l'aide d'une fonction sinus ou cosinus:
  \( x(t) = A\cos(\omega t + \varphi) \)
  
  Ici, \(A\) est l'amplitude du mouvement, \( \omega \) est la fréquence angulaire, \(t\) est le temps, et \( \varphi \) est l'angle de phase. L'angle de phase détermine la position initiale de l'objet à \(t = 0\). Le mouvement harmonique simple peut être analysé et prédit en utilisant des fonctions sinus et cosinus transformées.
• Exemple 3: Son et musique
  En acoustique, les ondes sonores peuvent être modélisées à l'aide de fonctions sinus et cosinus. La forme d'onde d'un son pur peut être représentée comme suit:
  \( y(t) = Asin(2 \pi f \cdot t + \varphi ) \)
  
  Ici, \(A\) est l'amplitude de l'onde sonore, qui détermine le volume ; \(f\) est la fréquence de l'onde sonore, qui détermine la hauteur ; \(t\) est la variable temporelle, et \( \varphi \) est l'angle de phase, qui détermine la position initiale de l'onde. En transformant les fonctions sinus et cosinus, nous pouvons analyser et synthétiser des sons et de la musique complexes.

Graphes des fonctions tangente et cotangente ☰

La tangente et la cotangente sont des fonctions trigonométriques qui sont liées aux fonctions sinus et cosinus. Elles sont périodiques et présentent des propriétés uniques qui les rendent intéressantes à étudier. Voici un examen approfondi des graphes de ces deux fonctions:

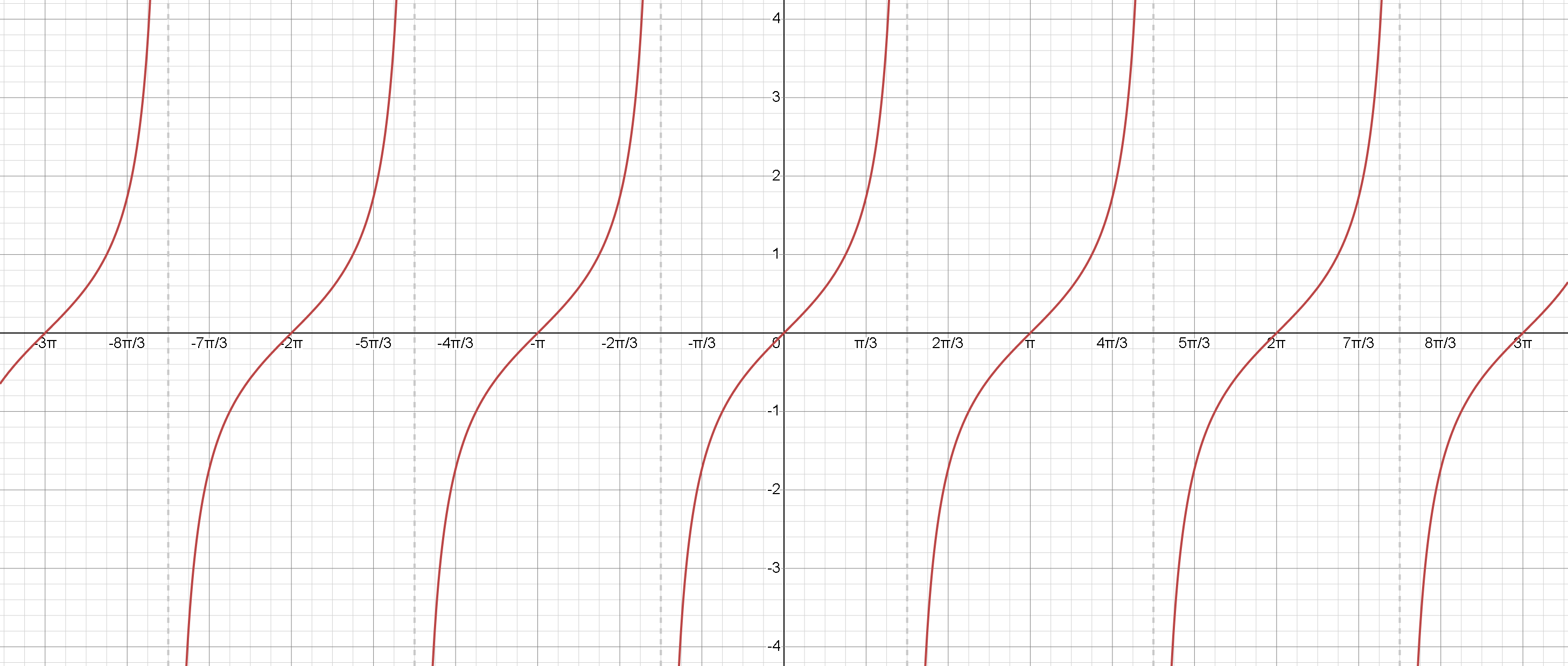
1. Fonction tangente \( \tan(x) \):
La fonction tangente est définie comme le rapport de la fonction sinus à la fonction cosinus, c'est-à-dire
\( \tan(x) = \frac{\sin(x)}{\cos(x)} \)

Caractéristiques clés du graphe de la tangente:

• Période: La fonction tangente a une période de \( \pi \), ce qui signifie qu'elle se répète tous les \( \pi \) unités le long de l'axe des \(x\).
• Asymptotes: Comme la fonction tangente est le rapport de sinus et cosinus, elle est indéfinie lorsque la fonction cosinus est égale à zéro. Cela se produit aux multiples impairs de \( \frac{\pi}{2} \). ( \( \pm \frac{\pi}{2} \), \( \pm \frac{3\pi}{2} \), et ainsi de suite).
  Ces points sont où se trouvent les asymptotes verticales.
• Plage: La plage de la fonction tangente est (\( -\infty ; \infty \)), car la fonction prend toutes les valeurs réelles.
• Symétrie: La fonction tangente est une fonction impaire, ce qui signifie qu'elle est symétrique par rapport à l'origine.
  En d'autres termes, \( \tan(-x) = -\tan(x) \)
• Augmentation: La fonction tangente augmente toujours sur chacune de ses périodes.

2. Fonction cotangente \( \cot(x) \):
La fonction cotangente est définie comme le rapport de la fonction cosinus à la fonction sinus, c'est-à-dire
\( \cot(x) = \frac{\cos(x)}{\sin(x)} \)

Caractéristiques clés du graphe de la cotangente:

• Période: La fonction cotangente a une période de \( \pi \), ce qui signifie qu'elle se répète tous les \( \pi \) unités le long de l'axe des \(x\), tout comme la fonction tangente.
• Asymptotes: Comme la fonction cotangente est le rapport de cosinus et sinus, elle est indéfinie lorsque la fonction sinus est égale à zéro. Cela se produit aux multiples entiers de \( \pi \). (0, \( \pm \pi \), \( \pm 2\pi \), et ainsi de suite). Ces points sont où se trouvent les asymptotes verticales.
• Plage: La plage de la fonction cotangente est \( (-\infty, \infty) \), car la fonction prend toutes les valeurs réelles.
• Symétrie: La fonction cotangente est une fonction impaire, ce qui signifie qu'elle est symétrique par rapport à l'origine.
  En d'autres termes, \( \cot(-x) = -\cot(x) \).
• Décroissance: La fonction cotangente décroît toujours sur chacune de ses périodes.

En résumé, les fonctions tangente et cotangente sont périodiques, avec une période de \( \pi \), et présentent une symétrie impaire. Elles ont des asymptotes verticales et des comportements différents, la fonction tangente étant croissante tandis que la fonction cotangente est décroissante.

Fonctions trigonométriques inverses ☰

Les fonctions trigonométriques inverses, également appelées arc-fonctions ou fonctions anti-trigonométriques, sont les fonctions inverses des fonctions trigonométriques de base: sinus, cosinus et tangente. Ces fonctions permettent de trouver l'angle lorsque vous connaissez la valeur trigonométrique. Il existe six principales fonctions trigonométriques inverses:

1. Sinus inverse. \( \sin^{-1} (x) \) ou \( \arcsin(x) \):
L'inverse de la fonction sinus.
Domaine: \( [-1 , 1 ] \)
Plage: \( \left[- \frac{\pi}{2}, \frac{\pi}{2}\right] \)

2. Cosinus inverse. \( \cos^{-1} (x) \) ou \( arccos(x) \):
L'inverse de la fonction cosinus.
Domaine: \( [-1 , 1 ] \)
Plage: \( [ 0 , \pi ] \)

3. Tangente inverse. \( \tan^{-1} (x) \) ou \( arctan(x) \) :
L'inverse de la fonction tangente.
Domaine: \( (-\infty , \infty ) \)
Plage: \( \left(- \frac{\pi}{2}, \frac{\pi}{2}\right) \)

4. Cosécante inverse. \( \csc^{-1} (x) \) ou \( arccsc(x) \) :
L'inverse de la fonction cosécante (qui est la réciproque de la fonction sinus).
Domaine: \( (-\infty, -1] \cup [1, \infty) \)
Plage: \( \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right]\)

5. Sécanse inverse. \( \sec^{-1} (x) \) ou \( arcsec(x) \):
L'inverse de la fonction sécante (qui est la réciproque de la fonction cosinus).
Domaine: \( \left(-\infty, -1\right] \cup \left[1, \infty\right) \)
Plage: \( \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] \)

6. Cotangente inverse. \( \cot^{-1} (x) \) ou \( arccot(x) \):
L'inverse de la fonction cotangente.
Domaine: \( (-\infty , \infty ) \)
Plage: \( ( 0 , \pi ) \)


Propriétés des fonctions trigonométriques inverses:

⠐ Domaines et plages restreints: Pour rendre les fonctions trigonométriques inversibles, leurs domaines sont restreints, ce qui entraîne des plages restreintes pour les fonctions trigonométriques inverses.

⠐ Notation: Les fonctions trigonométriques inverses sont souvent désignées par un préfixe " \( ^{-1} \)" ou " \(arc\)" . Par exemple, \( \sin^{-1} (x) \) ou \( \arcsin(x) \) représentent la fonction sinus inverse.
Notez que \( \sin^{-1} (x) \) n'est PAS la même que \( \frac{1}{\sin(x)} \), qui est la fonction réciproque (cosécante).

⠐ Composition:
La composition d'une fonction trigonométrique et de sa fonction inverse résulte en la fonction identité, à condition que l'entrée soit dans la plage correcte:

\( \sin(\arcsin(x)) = x \), Si \(x\) est dans le domaine de \( \arcsin( [-1,1] ) \)

\( \arcsin ( \sin(x) ) = x \), Si \(x\) est dans la plage de \( \arcsin( [ -\frac{\pi}{2} , \frac{\pi}{2} ] ) \)

Des relations similaires s'appliquent aux autres fonctions trigonométriques inverses.

⠐ Différentiabilité:
Les fonctions trigonométriques inverses sont différentiables dans leurs domaines, sauf aux points où les fonctions trigonométriques originales ont des tangentes verticales.
Par exemple, les fonctions arcsinus et arccosinus ne sont pas différentiables en \(x=-1\) et \(x=1\), et la fonction arctangente n'est pas différentiable en \(x=- \infty \) et \(x= \infty \).

⠐ Symétrie:
Certaines fonctions trigonométriques inverses présentent une symétrie.
Par exemple:
\( \arctan(-x) = -\arctan(x) \): La fonction tangente inverse est une fonction impaire.

\( \text{arccot}(-x) = \pi - \text{arccot}(x) \): La fonction cotangente inverse présente un type spécifique de symétrie.

Les fonctions trigonométriques inverses sont essentielles pour résoudre des problèmes impliquant des triangles et la trigonométrie, surtout lorsque vous devez trouver un angle étant donné les longueurs des côtés ou d'autres valeurs trigonométriques. Elles sont utilisées dans divers domaines des mathématiques, de la physique et de l'ingénierie, comme le calcul différentiel et intégral, la géométrie et l'étude des phénomènes périodiques.

⠐ Dérivées :
Les dérivées des fonctions trigonométriques inverses sont essentielles en calcul, notamment pour résoudre des problèmes d'intégration impliquant des fonctions trigonométriques. Voici les dérivées des trois principales fonctions trigonométriques inverses:

\( \frac{d (\arcsin(x))}{dx} = \frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arccos(x))}{dx} = -\frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arctan(x))}{dx} = \frac{1}{1 + x^2} \)