Cube ☰

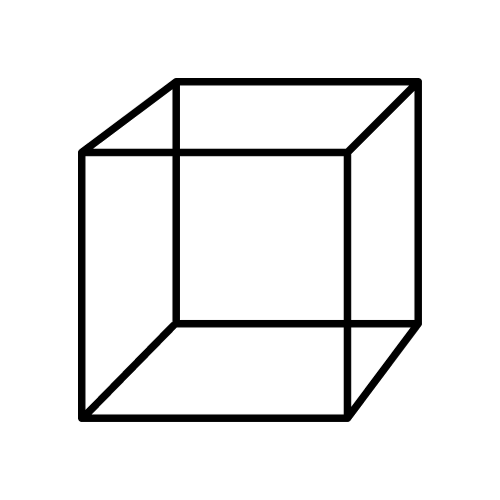
Formule du volume:

\(V=a^3\)

Aire de la surface du cube:

\(S=6a^2\)

Aire de la surface latérale du cube:

\(S=4a^2\)

Diagonale:

\(d= a \sqrt{3}\)

Définition:

Un parallélépipède rectangle avec des dimensions égales est appelé un cube. Il a 6 faces, chacune en forme de carré, 12 arêtes et 8 points de coin. Le nombre d'arêtes émanant d'un point unique est 3.

Parallélépipède ☰

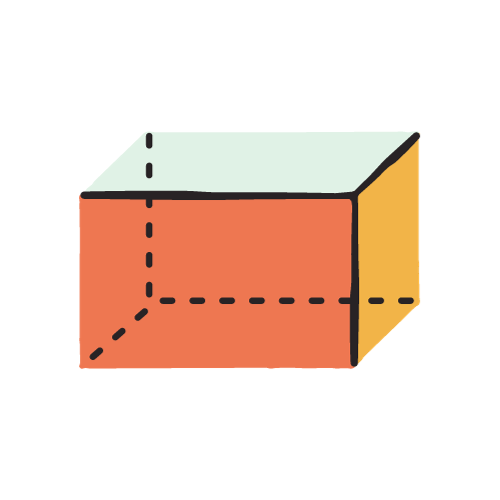
Formule du volume d'un parallélépipède rectangle:

\(V=a \cdot b \cdot c \)

Aire totale de la surface:

\( \small S = 2 \cdot ( a \cdot b + a \cdot c + b \cdot c) \)

Aire de la surface latérale:

\(S = 2 \cdot ( a \cdot c + b \cdot c ) \)

Diagonale:

Pour un Rectangle:

Diagonale (\( \small d\)) = \( \small \sqrt{{\text{Longueur}^2 + \text{Largeur}^2}}\)

Pour un Carré:

Diagonale (\( \small d\)) = \( \small \text{Côté} \times \sqrt{2}\)

Pour un Parallélogramme:

Diagonale 1 (\( \small d_1\)) = \( \small \text{Côté 1} \times \sqrt{2}\)

Diagonale 2 (\( \small d_2\)) = \( \small \text{Côté 2} \times \sqrt{2}\)

Pour un Cube:

Diagonale (\( \small d \)) = \( \small \text{Côté} \times \sqrt{3}\)

Pour une Boîte Rectangulaire (Parallélépipède Rectangle):

Diagonale (\( \small d\)) = \( \small \sqrt{{\text{Longueur}^2 + \text{Largeur}^2 + \text{Hauteur}^2}}\)

Pour un Losange:

Diagonale 1 (\( \small d_1\)) = \( \small 2 \times \text{Côté} \times \sin(\frac{\theta}{2})\), où \(\theta\) est l'un des angles.

Diagonale 2 (\( \small d_2\)) = \( \small 2 \times \text{Côté} \times \sin(90^\circ - \frac{\theta}{2})\)

Définition:

Un parallélépipède est une forme géométrique tridimensionnelle avec six faces en forme de parallélogramme. C'est un polyèdre, ce qui signifie qu'il a des faces plates, des arêtes droites et des coins (sommet) pointus. Le terme "parallélépipède" est souvent utilisé plus spécifiquement pour faire référence à un parallélépipède à six faces.

Les principales caractéristiques d'un parallélépipède sont les suivantes:

1. Six Faces: Un parallélépipède a six faces, qui sont des parallélogrammes. Ces faces viennent par paires, où chaque face est parallèle à une autre.

2. Arêtes: Il a 12 arêtes, qui sont les segments de droite où deux faces se rencontrent.

3. Sommets: Un parallélépipède a 8 sommets, qui sont les points où trois arêtes se rencontrent.

4. Faces opposées égales: Les faces opposées sont de même taille et de même forme, et elles sont parallèles les unes aux autres.

5. Angles droits: Les arêtes où les faces se rencontrent forment des angles droits.

6. Base Rectangulaire: Dans le contexte d'un parallélépipède rectangle, sa base se compose de quatre rectangles congruents à angles droits.

7. Trois Dimensions: Le parallélépipède est caractérisé par ses trois dimensions: longueur, largeur et hauteur.

Cylindre ☰

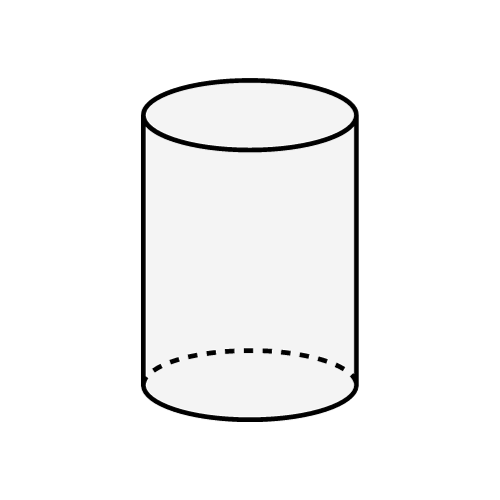
Formule du volume:

\(V= \pi r^2 \cdot h\)

Aire totale de la surface:

\( \small S = 2 \pi r \cdot h + 2 \cdot \pi r^2 = 2 \pi r(r+h) \)

Aire de la surface latérale:

\(S = 2 \pi r \cdot h \)

Définition:

Un cylindre est une forme géométrique tridimensionnelle avec deux bases circulaires parallèles et congruentes et une surface courbe reliant ces bases. C'est l'une des formes géométriques les plus courantes et fondamentales.

Caractéristiques essentielles d'un cylindre:

Deux Bases Circulaires: Un cylindre a deux extrémités circulaires plates qui sont identiques en taille et en forme. Ces bases sont parallèles entre elles.

Surface Courbe: La surface courbe du cylindre relie les deux bases circulaires. Elle forme une surface latérale qui est lisse et ne comporte pas de coins ni d'arêtes.

Axe: Le segment de droite reliant les centres des deux bases circulaires est appelé l'axe du cylindre. Il est perpendiculaire aux bases.

Hauteur: La hauteur du cylindre est la distance entre les deux bases circulaires le long de l'axe. C'est une mesure de la hauteur du cylindre.

Rayon: Le rayon est la distance du centre de l'une des bases circulaires au bord (ou périmètre) de cette base. Le rayon est le même pour les deux bases.

Prisme ☰

Formule du volume:

\(V= S_\text{base} \cdot h \)

Aire totale de la surface:

\( \small S = 2 S_\text{base} + S_\text{lateral} \)

Aire de la surface latérale:

\(S = P_\text{base} \cdot l \)

Définition:

Un prisme est une forme géométrique tridimensionnelle avec deux bases polygonales parallèles et congruentes et des faces rectangulaires ou parallélogrammes reliant les côtés correspondants des bases. Les caractéristiques essentielles d'un prisme sont les suivantes:

Deux Bases Polygonales: Un prisme a deux extrémités polygonales plates qui sont identiques en taille et en forme. Ces bases sont parallèles entre elles.

Faces Rectangulaires ou Parallélogrammes: Les faces du prisme relient les côtés correspondants des bases. Ces faces sont généralement de forme rectangulaire ou parallélogramme.

Arêtes: Les segments de droite où les faces se rencontrent sont appelés les arêtes du prisme.

Hauteur: La hauteur du prisme est la distance perpendiculaire entre les deux bases. C'est une mesure de la hauteur du prisme.

Faces Latérales: Les faces qui relient les côtés des bases sont appelées les faces latérales. Le nombre de faces latérales est égal au nombre de côtés dans les bases polygonales.

Sphère ☰

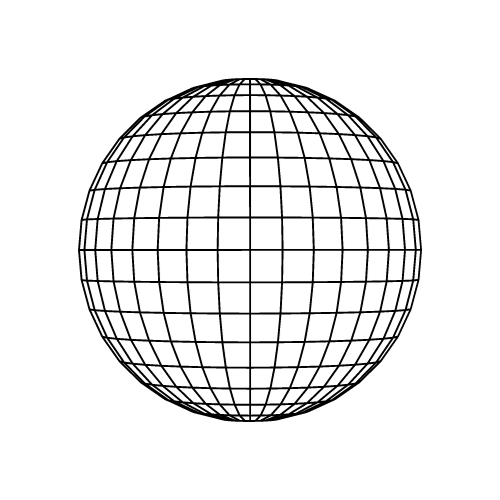
Formule du volume:

\( V = \frac{4}{3} \pi r^3 \)

Aire de la surface:

\( S = 4 \pi r^2 \)

Diamètre:

\( D=2r \)

Définition:

Une sphère est une forme géométrique tridimensionnelle parfaitement ronde et symétrique. Elle est caractérisée par plusieurs caractéristiques essentielles:

1. Rondeur: Une sphère est parfaitement ronde et n'a ni arêtes ni coins. Elle est définie comme l'ensemble de tous les points situés à une distance fixe (le rayon) d'un point central (le centre).

2. Centre: Le centre de la sphère est un point situé à égale distance de tous les points de la surface de la sphère.

3. Surface: La surface d'une sphère est l'ensemble de tous les points situés à la même distance fixe du centre. Elle forme une surface courbe continue sans côtés plats.

4. Rayon: Le rayon d'une sphère est la distance du centre à n'importe quel point de sa surface. Tous les rayons d'une sphère ont une longueur égale.

5. Diamètre: Le diamètre est une ligne droite passant par le centre de la sphère et reliant deux points de la surface de la sphère. Il est égal à deux fois le rayon.

Les sphères sont une forme géométrique fondamentale et se retrouvent dans divers aspects des mathématiques, des sciences et du monde physique. Elles ont des propriétés uniques, telles que le volume maximal pour une aire de surface donnée et une grande symétrie. Les sphères sont couramment rencontrées dans l'étude de la géométrie, de l'astronomie et de l'ingénierie.