Куб ☰

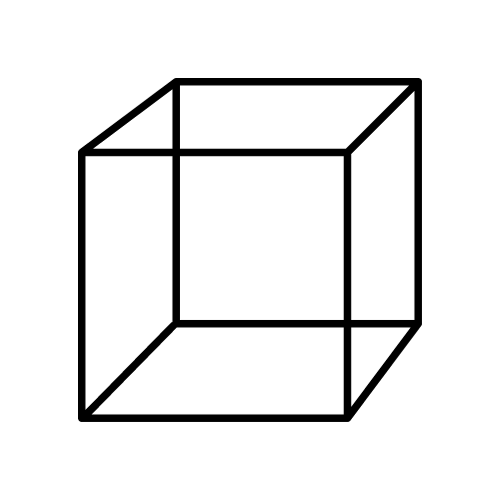
Формула объема:

\(V=a^3\)

Площадь поверхности куба:

\(S=6a^2\)

Площадь боковой поверхности куба:

\(S=4a^2\)

Диагональ:

\(d= a \sqrt{3}\)

Определение:

Прямоугольный параллелепипед с равными размерами называется кубом. У него 6 граней, каждая из которых имеет форму квадрата, 12 рёбер и 8 вершин. Количество рёбер, исходящих из одной точки, равно 3.

Параллелепипед ☰

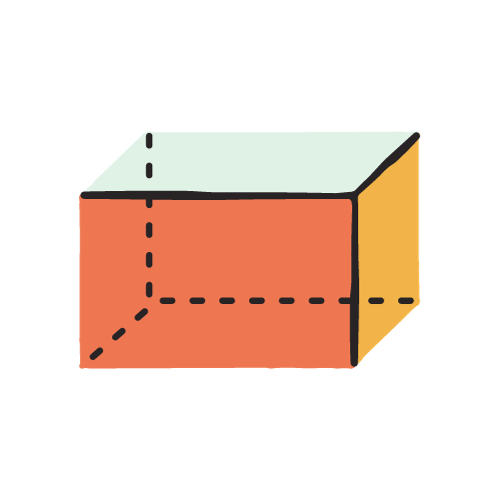
Формула объема прямоугольного параллелепипеда:

\(V=a \cdot b \cdot c \)

Полная площадь поверхности:

\( \small S = 2 \cdot ( a \cdot b + a \cdot c + b \cdot c) \)

Боковая площадь поверхности

\(S = 2 \cdot ( a \cdot c + b \cdot c ) \)

Диагональ:

Для Прямоугольника:

Диагональ (\( \small d\)) = \( \small \sqrt{{\text{Длина}^2 + \text{Ширина}^2}}\)

Для Квадрата:

Диагональ (\( \small d\)) = \( \small \text{Сторона} \times \sqrt{2}\)

Для Параллелограмма:

Диагональ 1 (\( \small d_1\)) = \( \small \text{Сторона 1} \times \sqrt{2}\)

Диагональ 2 (\( \small d_2\)) = \( \small \text{Сторона 2} \times \sqrt{2}\)

Для Куба:

Диагональ (\( \small d \)) = \( \small \text{Сторона} \times \sqrt{3}\)

Для Прямоугольной коробки (Прямоугольный параллелепипед):

Диагональ (\( \small d\)) = \( \small \sqrt{{\text{Длина}^2 + \text{Ширина}^2 + \text{Высота}^2}}\)

Для Ромба:

Диагональ 1 (\( \small d_1\)) = \( \small 2 \times \text{Сторона} \times \sin(\frac{\theta}{2})\), где \(\theta\) - один из углов.

Диагональ 2 (\( \small d_2\)) = \( \small 2 \times \text{Сторона} \times \sin(90^\circ - \frac{\theta}{2})\)

Определение:

Параллелепипед - это трехмерная геометрическая фигура с шестью параллелограммами в качестве граней. Это многогранник, что означает, что у него плоские грани, прямые ребра и острые углы (вершины). Термин "параллелепипед" часто используется более конкретно для обозначения шести гранных параллелепипедов.

Основные характеристики параллелепипеда следующие:

1. Шесть граней: У параллелепипеда шесть граней, которые являются параллелограммами. Эти грани идут парами, где каждая грань параллельна другой.

2. Рёбра: У него 12 рёбер, которые являются отрезками прямых, где пересекаются две грани.

3. Вершины: У параллелепипеда 8 вершин, которые представляют собой точки, где пересекаются три ребра.

4. Равные противоположные грани: Противоположные грани равны по размеру и форме, и они параллельны друг другу.

5. Прямые углы: Рёбра, где пересекаются грани, образуют прямые углы.

6. Прямоугольное основание: В контексте прямоугольного параллелепипеда его основание состоит из четырех прямоугольников, равных по размеру и форме.

7. Три измерения: Параллелепипед характеризуется своими тремя измерениями: длиной, шириной и высотой.

Цилиндр ☰

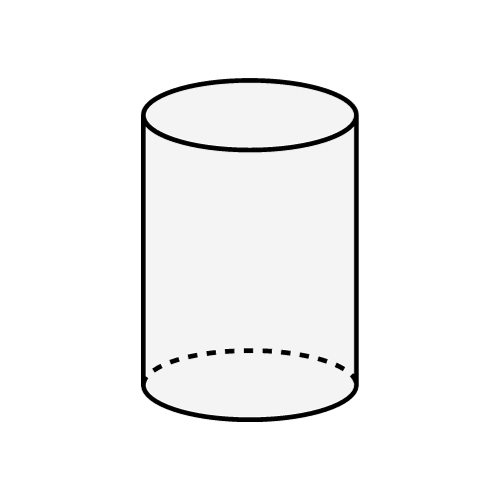
Формула объема:

\(V= \pi r^2 \cdot h\)

Полная площадь поверхности:

\( \small S = 2 \pi r \cdot h + 2 \cdot \pi r^2 = 2 \pi r(r+h) \)

Боковая площадь поверхности:

\(S = 2 \pi r \cdot h \)

Определение:

Цилиндр - это трехмерная геометрическая фигура с двумя параллельными и одинаковыми круглыми основаниями и изогнутой поверхностью, соединяющей эти основания. Это одна из самых распространенных и фундаментальных геометрических фигур.

Основные характеристики цилиндра:

Два Круглых Основания: У цилиндра два плоских круглых конца, которые идентичны по размеру и форме. Эти основания параллельны друг другу.

Изогнутая Поверхность: Изогнутая поверхность цилиндра соединяет два круглых основания. Она формирует боковую поверхность, которая гладкая и не имеет никаких углов или рёбер.

Ось: Отрезок прямой линии, соединяющий центры двух круглых оснований, называется осью цилиндра. Она перпендикулярна основаниям.

Высота: Высота цилиндра - это расстояние между двумя круглыми основаниями вдоль оси. Это мера того, насколько высоким является цилиндр.

Радиус: Радиус - это расстояние от центра одного из круглых оснований до края (или периметра) этого основания. Радиус одинаков для обоих оснований.

Призма ☰

Формула объема:

\(V= S_\text{основания} \cdot h \)

Полная площадь поверхности:

\( \small S = 2 S_\text{основания} + S_\text{боковая} \)

Боковая поверхность:

\(S = P_\text{основания} \cdot l \)

Определение:

Призма - это трехмерная геометрическая фигура с двумя параллельными и одинаковыми многоугольными основаниями и прямоугольными или параллелограммическими боковыми поверхностями, соединяющими соответствующие стороны оснований. Основные характеристики призмы следующие:

Два Многоугольных Основания: У призмы два плоских многоугольных конца, которые идентичны по размеру и форме. Эти основания параллельны друг другу.

Прямоугольные или Параллелограммические Боковые Поверхности: Поверхности призмы соединяют соответствующие стороны оснований. Эти поверхности обычно имеют форму прямоугольника или параллелограмма.

Рёбра: Отрезки прямых линий, где соединяются поверхности, называются рёбрами призмы.

Высота: Высота призмы - это перпендикулярное расстояние между двумя основаниями. Это мера того, насколько высокой является призма.

Боковые Поверхности: Поверхности, соединяющие стороны оснований, называются боковыми поверхностями. Количество боковых поверхностей равно количеству сторон в многоугольных основаниях.

Сфера ☰

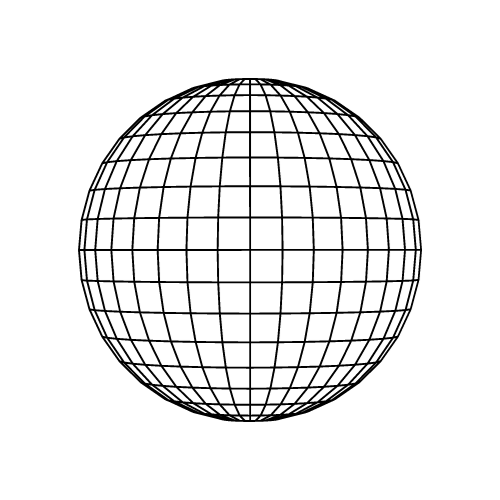
Формула объема:

\( V = \frac{4}{3} \pi r^3 \)

Площадь поверхности:

\( S = 4 \pi r^2 \)

Диаметр:

\( D=2r \)

Определение:

Сфера - это трехмерная геометрическая фигура, которая идеально круглая и симметричная. Она характеризуется несколькими основными чертами:

1. Круглость: Сфера идеально круглая и не имеет рёбер или углов. Она определяется как множество всех точек, находящихся на фиксированном расстоянии (радиусе) от центральной точки (центра).

2. Центр: Центр сферы - это точка, расположенная на равном расстоянии от всех точек поверхности сферы.

3. Поверхность: Поверхность сферы - это множество всех точек, находящихся на одинаковом фиксированном расстоянии от центра. Она образует непрерывную кривую поверхность без плоских сторон.

4. Радиус: Радиус сферы - это расстояние от центра до любой точки на ее поверхности. Все радиусы сферы имеют одинаковую длину.

5. Диаметр: Диаметр - это прямая линия, проходящая через центр сферы и соединяющая две точки на поверхности сферы. Он равен удвоенному радиусу.

Сферы являются фундаментальной геометрической формой и встречаются в различных аспектах математики, науки и физического мира. Они обладают уникальными свойствами, такими как максимальный объем при заданной площади поверхности и высокая симметрия. Сферы часто встречаются при изучении геометрии, астрономии и инженерии.