Область и область значений функций ☰

Функция - это математический объект, который присваивает каждому входу уникальный выход. Множество всех возможных входов называется областью функции, а множество всех возможных выходов - областью значений функции. Другими словами, область - это множество значений, которые можно подставить в функцию, а область значений - множество значений, которые функция может произвести.
Формально функция \( f \) - это отображение из множества \( A \) (область) в множество \( B \) (область значений), где для каждого \( a \in A \) существует уникальное \( b \in B \) такое, что \( f(a)=b \). Мы пишем \( f \): \( A \rightarrow B \) для обозначения того, что \( f \) - это функция от \( A \) до \( B \).
Например, рассмотрим функцию \( f(x)=x^2 \), где \( x \) - это вещественное число. Область \( f \) является множеством всех вещественных чисел, потому что любое вещественное число можно подставить в \( f \). Однако область значений \( f \) - это только множество неотрицательных вещественных чисел, потому что \( f(x) \) всегда неотрицательно.
При поиске области и области значений функции нужно иметь в виду следующее:

• Область функции - это множество всех возможных входов. Это означает, что любое значение, которое делает функцию неопределенной (например, деление на ноль или извлечение квадратного корня из отрицательного числа), не может принадлежать области.
• Область значений функции - это множество всех возможных выходов. Это означает, что функция может производить только значения, которые находятся в области значений.
• Возможно, что у разных функций могут быть одинаковые области или области значений. Например, функции \( f(x)=x^2 \) и \( g(x)=|x| \) обе имеют область всех вещественных чисел, но их области значений разные.
• Область и область значений функции могут быть определены путем анализа графика функции. Область - это множество всех возможных значений \( x \), которые появляются на графике, и область значений - множество всех возможных значений \( y \), которые появляются на графике.

Давайте рассмотрим несколько примеров, чтобы лучше понять, как найти область и область значений функции.

Пример 1: Найдем область и область значений функции \( f(x) = \frac{1}{x} \)
Функция \( f(x) \) определена для всех \( x \neq 0 \), потому что деление на ноль неопределено. Следовательно, область \( f \) - это множество всех вещественных чисел, кроме нуля, или \( (-\infty ; 0) \cup (0 ; \infty ) \).
Чтобы найти область значений \( f \), мы отмечаем, что \( f(x) \) может быть любым вещественным числом, кроме нуля. Это означает, что область значений \( f \) также \( (-\infty ; 0 ) \cup ( 0 ; \infty ) \).

Пример 2: Найдем область и область значений функции \( f(x) = \sqrt{4-x^2} \).
Функция \( f(x) \) определена только для значений \( x \), таких что \( 4 - x^2 \ge 0 \). Решая это неравенство, мы получаем \( -2 \le x \le 2 \).
Следовательно, область \( f \) - это закрытый интервал \([-2,2]\). Чтобы найти область значений \( f \), мы отмечаем, что \( f(x) \) может быть любым неотрицательным вещественным числом, меньшим или равным 2. Это означает, что область значений \( f \) - это закрытый интервал \([0,2]\).

Пример 3: Найдем область и область значений функции \( f(x)=sin(x) \).
Функция \( f(x) \) определена для всех вещественных чисел, поэтому область \( f \) - это \( (-\infty , \infty) \).
Чтобы найти область значений \( f \), мы отмечаем, что \( sin(x) \) может принимать любое значение от -1 до 1 включительно. Следовательно, область значений \( f \) - это закрытый интервал \([-1,1] \).

В заключение, область функции - это множество всех возможных входов, а область значений - множество всех возможных выходов. Область и область значений могут быть определены путем анализа самой функции или ее графика.

Свойства функций ☰

У функций есть различные свойства, которые могут использоваться для их анализа и сравнения. В этом объяснении мы рассмотрим некоторые из наиболее важных свойств функций.

Четные и нечетные функции:
Функция \(f\) называется четной, если \(f(-x)=f(x) \) для всех \(x\) в области определения \(f\). Другими словами, функция симметрична относительно оси \(y\). Примером четной функции является \(f(x)=x^2 \).
Функция \(f\) называется нечетной, если \(f(-x)=-f(x) \) для всех \(x\) в области определения \(f\). Другими словами, функция симметрична относительно начала координат. Примером нечетной функции является \(f(x)=x^3 \).

Возрастающие и убывающие функции:
Функция \(f\) называется возрастающей на интервале, если \( f(x_1 ) < f(x_2 ) \) всегда, когда \(x_1 < x_2\) и \(x_1, x_2 \) находятся в области определения \(f\). Другими словами, функция растет при увеличении \(x\). Примером возрастающей функции является \(f(x)=x \).
Функция \(f\) называется убывающей на интервале, если \( f(x_1 ) > f(x_2 ) \) всегда, когда \(x_1 < x_2\) и \(x_1, x_2 \) находятся в области определения \(f\). Другими словами, функция убывает при увеличении \(x\). Примером убывающей функции является \(f(x)=-x \).

Периодические функции:
Функция \(f\) называется периодической, если существует положительное число \(p\), такое что \(f(x+p)=f(x)\) для всех \(x\) в области определения \(f\). Другими словами, функция повторяется после фиксированного интервала. Примером периодической функции является \(f(x)=sin(x)\).

Инъективные и сюръективные функции:
Функция \(f\) называется инъективной (или однозначной), если для каждого \(y\) в области значений \(f\) существует ровно один \(x\) в области определения \(f\), такой что \(f(x)=y\). Другими словами, ни один из двух различных входов не дает одинакового вывода. Примером инъективной функции является \( f(x)=x+1 \).
Функция \(f\) называется сюръективной (или на), если для каждого \(y\) в области значений \(f\) существует хотя бы один \(x\) в области определения \(f\), такой что \(f(x)=y\). Другими словами, каждый вывод в области значений достигается некоторым входом. Примером сюръективной функции является \( f(x)=x^2 \).

Биективные функции:
Функция \(f\) называется биективной, если она одновременно инъективна и сюръективна. Другими словами, каждый вывод в области значений достигается ровно одним входом. Примером биективной функции является \( f(x)= \sqrt{x} \).

В заключение, свойства функций могут использоваться для описания различных аспектов функции, таких как ее симметрия, направление, повторение и соответствие между входами и выходами. Понимание этих свойств может помочь в анализе и сравнении функций в различных контекстах.

Классификация функций ☰

Функции могут быть классифицированы на основе их свойств и поведения. В этом объяснении мы рассмотрим наиболее распространенные классификации функций.

Постоянная функция:
\(F(x) = c.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = \{c\}.\)


Линейная функция:
\(F(x) = x.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Нули: \( x=0 \).
Увеличивается.
Без экстремума.


Функция модуля:
\(F(x) = |x|.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = [0, +\infty).\)
Нули: \(x = 0.\)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Точка минимума: \((0, 0).\)


Рациональная функция:
\(F(x) = \frac{1}{x}.\)
\(D(f) = (-\infty, 0) \cup (0, +\infty).\)
\(E(f) = (-\infty, 0) \cup (0, +\infty).\)
\((- \infty, 0) \downarrow \text{, } (0, +\infty) \downarrow.\)
Нет нулей.
Без экстремума.


Квадратичная функция:
\(F(x) = x^2.\)
\( D(f) = (-\infty, +\infty). \)
\(E(f) = [0, +\infty). \)
\((- \infty, 0] \downarrow \text{, } [0, +\infty) \uparrow.\)
Нули: \(x = 0.\)
Точка минимума: \((0, 0).\)


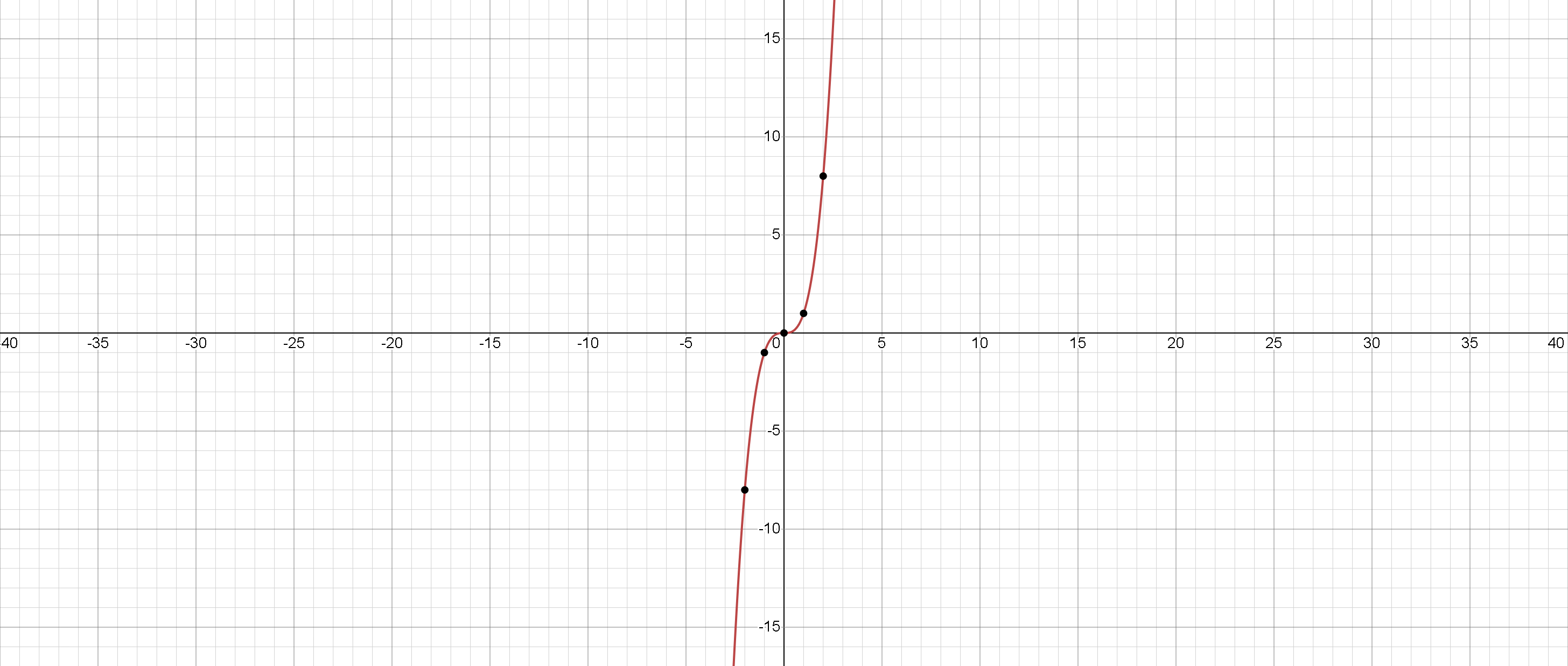
Кубическая функция:
\(F(x) = x^3.\)
\(D(f) = (-\infty, +\infty).\)
\(E(f) = (-\infty, +\infty).\)
Нули: \(x = 0.\)
Увеличивается.
Без экстремума.


Квадратный корень функция:
\(F(x) = \sqrt{x}.\)
\(D(f) = [0; +\infty).\)
\(E(f) = [0; +\infty).\)
Нули: \(x = 0.\)
\([0; +\infty) \uparrow \).
Без экстремума.


Тригонометрические функции:
Тригонометрическая функция - это функция, которая включает в себя отношения сторон прямоугольного треугольника. Примеры тригонометрических функций включают \( sin(x) \), \( cos(x) \) и \( tan(x) \). Графики тригонометрических функций периодичны и повторяются после фиксированного интервала.

Кусочные функции:
Кусочная функция - это функция, которая определяется разными уравнениями на разных частях своей области определения.

Примеры кусочных функций включают:
\( f(x) = \begin{cases} 2x + 1 & \text{if } x < 0 \\ 3x & \text{if } x \geq 0 \end{cases} \)

\( f(x) = \begin{cases} x^2 & \text{if } x \leq -1 \\ -x & \text{if } -1 < x < 1 \\ x & \text{if } x \geq 1 \end{cases} \)

Степенные функции или мономы ☰

Эти функции (\( y = x^n \)) также известны как степенные функции или мономы.
Значение показателя степени \(n\) определяет форму и поведение функции. Когда \(n\) - положительное целое число, функция представляет собой полином с одним членом, известным как моном. Степень полинома равна значению \(n\).

\( F(x)= x^{2k} \):
\( D(f) = (-\infty ; +\infty) \).
\( E(f) = [0; +\infty). \)
Нули: \(x=0 \).
\( (-\infty; 0] \downarrow \text{, } [0; +\infty) \uparrow \).
\( x_{\text{min}} = 0, f_{\text{min}} = 0 \).
Без экстремума.

\( F(x) = x^{2k+1} \):
\( D(f) = (-\infty ; +\infty). \)
\( E(f) = (-\infty ; +\infty). \)
Нули: \( x=0 \).
\( (-\infty ; +\infty) \uparrow \)
Без экстремума.

Например, функция \(y=x^2\) представляет собой параболу, которая является кривой формы U и открывается вверх. Эта функция имеет минимальное значение при \(x=0\) и увеличивается без ограничений по мере удаления \(x\) от нуля в любом направлении.
Когда \(k\) является отрицательным целым числом, функция представляет собой обратную величину монома. Например, функция \(y = x^{-1} \) представляет собой обратную функцию, также известную как обратная функция. Эта функция имеет вертикальную асимптоту при \(x=0\), где функция приближается к положительной или отрицательной бесконечности в зависимости от знака \(x\). Обратная функция симметрична относительно прямой \(y=x\).
Когда \(2k =n\) или \(2k+1 = n\) является дробью, функция представляет собой радикальную функцию, где числитель дроби определяет степень корня, а знаменатель определяет степень \(x\). Например, функция \( y = x^\frac{1}{2} \) представляет собой функцию квадратного корня, которая имеет область определения неотрицательных действительных чисел и область значений неотрицательных действительных чисел. Функция квадратного корня представляет собой полупараболу, которая открывается вправо и имеет вертикальную асимптоту при \(x=0\).
В целом, семейство функций \(y=x^n\) демонстрирует различные поведения в зависимости от значения \(n\). График этих функций может иметь различные формы, включая прямые линии, кривые и разрывные скачки. Изучение этих функций важно в математике и науке, так как они встречаются во многих естественных явлениях и инженерных приложениях.

Некоторые важные свойства этих функций включают:

• Когда \(n\) четное число, функция \(y=x^n\) всегда неотрицательна для всех действительных значений \(x\). Когда \(n\) - нечетное число, функция может принимать как положительные, так и отрицательные значения в зависимости от знака \(x\).
• Когда \(n\) положительное число, функция \(y=x^n\) возрастает на интервале \( (0, \infty) \) и убывает на интервале \( (-\infty, 0) \). Когда \(n\) отрицательное число, функция ведет себя наоборот.
• Производная функции \(y=x^n\) задается формулой \( y'=nx^{n-1} \). Это означает, что наклон касательной к функции в любой точке пропорционален значению показателя степени \(n\).
• Интеграл функции \(y=x^n\) задается формулой \( \int x^n \, dx = \frac{x^{(n+1)}}{(n+1)} + C \), где \(C\) - постоянная интеграции. Эта формула справедлива для всех значений \(n\) за исключением случая, когда \(n=-1\), в котором интеграл задается формулой \( ln|x|+C \).

В заключение, семейство функций \(y=x^n\) является фундаментальной темой в математике, с множеством важных приложений в различных областях. Поведение и свойства этих функций зависят от значения показателя степени \(n\), который определяет форму графика и другие важные характеристики.

Операции над функциями ☰

В математике операции над функциями относятся к математическим операциям, которые можно выполнять с функциями. Эти операции могут использоваться для изменения или комбинирования функций для создания новых функций. Самые распространенные операции над функциями включают сложение, вычитание, умножение, деление, композицию и обратную функцию.

Сложение и вычитание функций:
Функции могут быть сложены или вычтены, чтобы создать новую функцию. Для двух функций \(f(x)\) и \(g(x)\), сумма или разность двух функций обозначается как \( (f \pm g)(x) \) и определяется как:
\( (f+g) (x) = f(x)+ g(x) \)
\( (f-g) (x) = f(x)- g(x) \)
Сумма двух четных функций является четной, а сумма двух нечетных функций является нечетной.

Например: \( f(x) = x+1 \) и \( g(x) = 2x-3 \) функции.
\( \small (f+g) (x) = f(x) + g(x) = (x+1) + (2x-3) =\) \( 3x-2 \)
\( \small (f-g) (x) = f(x) - g(x) = (x+1) - (2x-3) =\) \( -x+4 \)

Умножение и деление функций:
Функции также могут быть умножены или поделены, чтобы создать новые функции. Для двух функций \(f(x)\) и \(g(x)\), произведение или частное двух функций обозначается как \( (f \cdot g) (x) \) или \( (\frac{f}{g}) (x) \) и определяется как:
\( (f \cdot g)(x) = f(x) \cdot g(x) \)
\( ( \frac{f}{g} )(x) = \frac{f(x)}{g(x)}, \quad g(x) \neq 0 \)

Произведение (частное) двух четных функций и двух нечетных функций является четной функцией, а произведение (частное) четной функции и нечетной функции является нечетной функцией.

Например: \( f(x) = x+1 \) и \( g(x) = 2x-3 \) функции.
\( (f \cdot g)(x) = (x+1)(2x-3) = 2x^2 - x - 3 \)
\( (\frac{f}{g})(x) = \frac{x+1}{2x-3} \)

Композиция функций:
Композиция функций - это операция объединения двух или более функций для создания новой функции. Для двух функций \( f(x) \) и \( g(x) \), композиция двух функций обозначается как \( (f \circ g)(x) \) и определяется как: \( (f \circ g)(x) = f(g(x)) \).

Например: \( f(x) = x^2 \) и \( g(x) = x+1 \) функции.
\( (f \circ g) (x) = f(g (x) ) = f(x+1) = (x+1)^2 \)
Обратите внимание, что порядок композиции имеет значение, т.е. \( (f \circ g)(x) \) не равно \( (g \circ f)(x) \).

Обратная функция:
Обратная функция - это новая функция, которая "отменяет" исходную функцию. Для функции \(f(x) \), обратная функция обозначается как \(f^{-1} (x) \) и определяется как:
\( f^{-1} (f(x)) = x \)

Для того чтобы обратная функция существовала, функция должна быть инъективной. Функция является инъективной, если каждый элемент области определения сопоставляется с уникальным элементом в области значений. Обратная функция является отражением функции относительно прямой \(y=x\).
Например: Если \( f(x) = 2x+1 \) , то \( f^{-1} (x) = \frac{x-1}{2} \)
Чтобы проверить это, мы можем убедиться, что \( f^{-1} (f(x))= \frac{2x+1-1}{2} = x \).

Вот некоторые дополнительные детали об операциях над функциями:

Свойства операций над функциями:
Операции над функциями имеют некоторые свойства, которые делают их полезными для решения математических задач. К ним относятся:

• Ассоциативность: Порядок выполнения операций не влияет на результат.
  Например, \( (f+g)+h = f+(g+h) \)
• Коммутативность: Порядок функций не влияет на результат.
  Например, \( f+g=g+f \)
• Дистрибутивность: Операция распространяется на другую операцию.
  Например, \( f \cdot (g+h) = f \cdot g + f \cdot h \)

Области и области значений:
При выполнении операций над функциями важно учитывать области и области значений функций. Область определения функции - это набор значений, для которых функция определена, в то время как область значений - это набор значений, которые может принимать функция.
При сложении или вычитании функций области и области значений функций должны быть одинаковыми. При умножении или делении функций областью результата функции должно быть пересечение областей определения двух функций, а областью значений результата функции может быть ограничена областью значений знаменателя.
При составлении функций область значений внутренней функции должна быть подмножеством области определения внешней функции.

Преобразования функций:
Операции над функциями также могут использоваться для преобразования функций. Например, добавление константы к функции сдвигает функцию вертикально, а умножение функции на константу масштабирует функцию вертикально. Аналогично, добавление переменной к функции сдвигает функцию горизонтально, а умножение функции на переменную масштабирует функцию горизонтально.