Многоугольник ☰

Многоугольник - это двумерная геометрическая фигура, состоящая из конечного числа отрезков (называемых сторонами или ребрами), которые соединены концами, образуя замкнутую форму. Слово "многоугольник" происходит от греческих слов "поли" (что означает "много") и "гон" (что означает "угол").
Многоугольники могут иметь любое количество сторон, но они должны быть прямыми линиями и не могут пересекаться. Многоугольники с тремя сторонами называются треугольниками, с четырьмя сторонами - четырехугольниками, с пятью сторонами - пятиугольниками и так далее.
Периметр многоугольника - это сумма длин его сторон. Если у многоугольника \(n\) сторон и длина каждой стороны обозначается \(s_i\) для \(i = 1,2,…,n,\) , то периметр \(P\) задается формулой: $$ P = s_1 + s_2 + \ldots + s_n = \sum_{i=1}^n s_i $$

Внутренние углы многоугольника - это углы, образованные любыми двумя смежными сторонами внутри многоугольника. Сумма внутренних углов многоугольника с \(n\) сторонами задается формулой: $$ \sum_{i=1}^n \theta_i =(n-2) \cdot 180^\circ $$ где \( \theta_i \) - это мера \(i\)-го внутреннего угла в градусах.

Регулярные многоугольники - это многоугольники, у которых все стороны имеют одинаковую длину, а все внутренние углы имеют одинаковую меру. Мера каждого внутреннего угла регулярного многоугольника с \(n\) сторонами задается формулой: $$ \theta = \frac{(n-2) \cdot 180^\circ }{n} $$

Площадь многоугольника может быть рассчитана несколькими способами, в зависимости от формы многоугольника.
Например, площадь треугольника может быть рассчитана с использованием формулы: \( A = \frac{1}{2} bh \) , где \(b\) - это основание треугольника, а \(h\) - его высота.
Площадь регулярного многоугольника с \(n\) сторонами и длиной стороны \(s\) может быть рассчитана с использованием формулы: \( A= \frac{1}{4} ns^2 cot(\frac{\pi }{n}) \), где \(cot(x)\) - это функция котангенс.

Многоугольники используются во многих различных областях, включая математику, инженерию и компьютерную графику. Они также используются в повседневной жизни, например, в дизайне зданий и мебели.

Выпуклые и вогнутые многоугольники. ☰

Многоугольники можно классифицировать как выпуклые или вогнутые на основе характера их углов.
Выпуклый многоугольник - это многоугольник, у которого все его внутренние углы меньше 180 градусов. Другими словами, если провести прямую линию между любыми двумя точками внутри многоугольника, то отрезок всегда будет полностью лежать внутри многоугольника. Таким же образом, выпуклый многоугольник - это многоугольник, который не "сгибается внутрь", как ложка.
Примерами выпуклых многоугольников являются равносторонние треугольники, квадраты, правильные пятиугольники и правильные шестиугольники. Выпуклые многоугольники важны во многих областях математики и приложений, поскольку они имеют много полезных свойств и относительно легко обрабатываются.
С другой стороны, вогнутый многоугольник - это многоугольник, у которого хотя бы один из его внутренних углов больше 180 градусов. Другими словами, если провести прямую линию между любыми двумя точками внутри многоугольника, то отрезок пересечет границу многоугольника. Таким же образом, вогнутый многоугольник - это многоугольник, который "сгибается внутрь", как ложка.
Примерами вогнутых многоугольников являются буква "С" (когда она изображена в виде замкнутой формы), буква "L" и любой многоугольник с "выемкой" или "вмятиной" в его границе. Вогнутые многоугольники менее распространены в приложениях, поскольку у них более сложная геометрия и их математическая обработка может быть сложнее.
Одно важное различие между выпуклыми и вогнутыми многоугольниками заключается в том, что у выпуклых многоугольников есть уникальная центральная точка, называемая центроидом, которая также является центром баланса или гравитации многоугольника. Это делает выпуклые многоугольники полезными в приложениях, таких как инженерия и архитектура, где баланс и стабильность играют важную роль. С другой стороны, у вогнутых многоугольников нет уникального центроида, что делает их более сложными для анализа и работы.

Сумма внутренних углов выпуклого многоугольника ☰

Сумма внутренних углов выпуклого многоугольника с \(n\) сторонами задается формулой: $$ \sum_{i=1}^n \theta_i =(n-2)⋅180^\circ $$ где \( \theta_i\) - это мера \(i\)-го внутреннего угла в градусах.
Сумма внешних углов выпуклого многоугольника всегда равна 360 градусам, независимо от количества сторон. Это означает, что если измерить каждый внешний угол выпуклого многоугольника и сложить их меры, то общая сумма всегда будет равна 360 градусам.
Чтобы понять, почему это так, представьте себе, что вы идете вдоль периметра многоугольника и поворачиваетесь на каждой вершине, чтобы продолжить следующую сторону. При каждом повороте вы создаете внешний угол с стороной, от которой вы только что отошли. Если вы сделаете полный круг вокруг многоугольника, то совершите общий поворот на 360 градусов.
Мы можем использовать формулу для суммы внутренних углов и тот факт, что сумма внешних углов равна 360 градусам, чтобы найти меру каждого внешнего угла. Пусть \(a_i\) - это мера \(i\)-го внешнего угла в градусах. Тогда у нас есть: $$ \sum_{i=1}^n \theta_i + \sum_{i=1}^n a_i =(n-2) \cdot 180^\circ +360^\circ $$ $$ \small \sum_{i=1}^n a_i =(\sum_{i=1}^n \theta_i )-(n-2) \cdot 180^\circ +360^\circ = (n-2) \cdot 180^\circ -(n-2) \cdot 180^\circ +360^\circ=360^\circ $$ Следовательно, мера каждого внешнего угла выпуклого многоугольника задается формулой: $$ a_i= 360^\circ - \theta_i $$ Обратите внимание, что эта формула применяется только к выпуклым многоугольникам, а не к вогнутым многоугольникам, у которых внешние углы могут быть больше 180 градусов.

Вписанные и описанные многоугольники ☰

Вписанные и описанные многоугольники - важные концепции в геометрии, которые включают в себя многоугольники, вписанные внутрь и описанные вокруг круга. Эти концепции часто используются в различных областях математики, таких как геометрия, тригонометрия и исчисление.

Вписанный многоугольник
Вписанный многоугольник - это многоугольник, который нарисован внутри круга так, чтобы все его вершины лежали на окружности круга. Ниже приведен пример вписанного многоугольника.


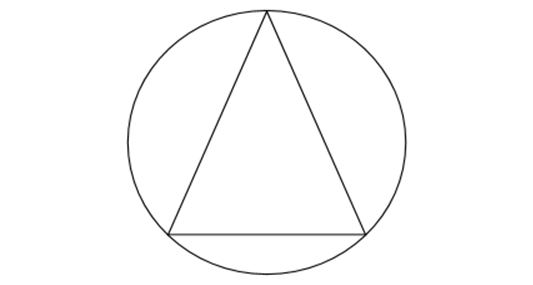
Основное свойство вписанного многоугольника заключается в том, что сумма внутренних углов равна \( (n-2) 180^\circ \), где \(n\) - количество сторон многоугольника. Это известно как сумма внутренних углов многоугольника. Мы можем доказать это свойство, используя тот факт, что центральный угол круга, подразумеваемый каждой стороной многоугольника, равен соответствующему внутреннему углу многоугольника. Поскольку сумма центральных углов составляет \( 360^\circ \) (полный угол круга), сумма внутренних углов должна быть \( (n-2) 180^\circ \).
Еще одно важное свойство вписанного многоугольника заключается в том, что произведение длин его сторон максимизируется, когда многоугольник является правильным. Иными словами, если \(s_1\), \(s_2\), … , \(s_n\) - длины сторон вписанного многоугольника с \(n\) сторонами, то произведение \(s_1\), \(s_2\), … , \(s_n\) максимизируется, когда многоугольник является правильным.

Описанный многоугольник
Описанный многоугольник - это многоугольник, нарисованный за пределами круга так, чтобы все его вершины лежали на окружности круга. Ниже приведен пример описанного многоугольника.


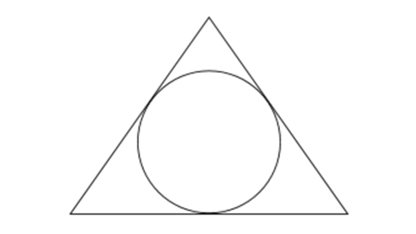
Основное свойство описанного многоугольника заключается в том, что произведение длин его сторон равно \( 2R^n sin( \frac{360^\circ}{n} ) \), где \(n\) - количество сторон многоугольника, а \(R\) - радиус окружности. Это известно как формула произведения сторон многоугольника. Мы можем доказать эту формулу, используя тот факт, что длина каждой стороны многоугольника равна удвоенному радиусу, умноженному на синус половины центрального угла круга, подразумеваемого этой стороной. Поскольку центральный угол правильного многоугольника с \(n\) сторонами равен \( \frac{360^\circ}{n} \) , у нас есть вышеуказанная формула.
Еще одно важное свойство описанного многоугольника заключается в том, что площадь многоугольника максимизируется, когда многоугольник является правильным. Иными словами, если \(A\) - площадь описанного многоугольника с \(n\) сторонами, то площадь максимизируется, когда многоугольник является правильным.

Примеры
Давайте рассмотрим пример, чтобы проиллюстрировать эти концепции. Предположим, у нас есть круг с радиусом 5. Какова максимальная площадь вписанного пятиугольника (многоугольника с пятью сторонами) в этом круге, и какова максимальная площадь описанного пятиугольника?

Чтобы найти максимальную площадь вписанного пятиугольника, нам нужно найти длину стороны, которая максимизирует произведение длин сторон. Поскольку пятиугольник вписан в круг радиусом 5, длина стороны определяется $$s =2R sin(\frac{180^\circ}{5} ) = 2 \cdot 5sin(36^\circ )= 6.472 $$ Следовательно, максимальная площадь вписанного пятиугольника достигается, когда пятиугольник является правильным, и составляет: $$ A_\text{вписан} = \frac{5s^2}{4} \cdot tan(36^\circ ) \approx 61.937 $$ Чтобы найти максимальную площадь описанного пятиугольника, мы можем использовать формулу произведения сторон многоугольника. Для пятиугольника у нас есть: $$ \small A_\text{описан} =\frac{5s^2}{4} \cdot cot(36^\circ )=5R^2 sin(72^\circ ) \approx 78.589 $$ Снова максимальная площадь описанного пятиугольника достигается, когда пятиугольник является правильным.

В заключение, вписанные и описанные многоугольники - важные концепции в геометрии, которые включают в себя многоугольники, вписанные внутрь и описанные вокруг круга. Эти концепции имеют множество интересных свойств и используются в различных областях математики.

Круги, нарисованные внутри и снаружи треугольника ☰

Тема о кругах, нарисованных внутри и снаружи треугольника, является важным аспектом элементарной геометрии. Существует несколько теорем, связанных с кругами, нарисованными внутри и снаружи треугольника, которые обсуждаются ниже:

Вписанный круг и центр вписанного круга:
Вписанный круг треугольника - это круг, касающийся всех трех сторон треугольника. Центр вписанного круга называется центром вписанного круга треугольника. Центр вписанного круга находится на равном расстоянии от всех трех сторон треугольника.

Теорема 1: Центр вписанного круга треугольника является пересечением его трех биссектрис углов.

Доказательство: Пусть ABC - треугольник, а I - центр его вписанного круга. Пусть D, E и F - точки касания вписанного круга с сторонами BC, AC и AB соответственно. Тогда ID, IE и IF являются перпендикулярными биссектрисами отрезков EF, FD и DE соответственно. Следовательно, ID является биссектрисой угла BIC, где B и C - вершины треугольника, а I - центр вписанного круга. Аналогично, IE и IF являются биссектрисами углов AIC и AIB соответственно. Следовательно, три биссектрисы углов треугольника пересекаются в центре I.

Теорема 2: Расстояние от центра вписанного круга треугольника до любой его стороны равно радиусу вписанного круга.

Доказательство: Пусть ABC - треугольник, а I - центр его вписанного круга. Пусть D, E и F - точки касания вписанного круга со сторонами BC, AC и AB соответственно. Тогда ID, IE и IF являются перпендикулярными биссектрисами отрезков EF, FD и DE соответственно. Следовательно, ID является высотой треугольника IBC от вершины I до стороны BC. Аналогично, IE и IF являются высотами треугольников AIC и AIB от вершины I до сторон AC и AB соответственно. Поскольку \(ID=IE=IF\), следует, что расстояние от центра I до любой стороны треугольника равно радиусу вписанного круга.

Описанный круг и центр описанного круга:
Описанный круг треугольника - это круг, проходящий через все три вершины треугольника. Центр описанного круга называется центром описанного круга треугольника. Центр описанного круга - это пересечение перпендикулярных биссектрис сторон треугольника.

Теорема 3: Центр описанного круга треугольника является пересечением перпендикулярных биссектрис его сторон.

Доказательство: Пусть ABC - треугольник, а O - центр его описанного круга. Пусть D, E и F - середины сторон BC, AC и AB соответственно. Тогда OD, OE и OF являются перпендикулярными биссектрисами сторон BC, AC и AB соответственно. Следовательно, OD перпендикулярен BC, и \(OD=\frac{1}{2} BC\). Аналогично, OE перпендикулярен AC, и \(OE=\frac{1}{2} AC\). Аналогично, OF перпендикулярен AB, и \( OF= \frac{1}{2} AB \). Следовательно, O находится на равном расстоянии от всех трех вершин треугольника и, следовательно, лежит на перпендикулярных биссектрисах всех трех сторон. Следовательно, центр описанного круга треугольника является пересечением перпендикулярных биссектрис его сторон.

Теорема 4: Перпендикулярные биссектрисы сторон треугольника пересекаются тогда и только тогда, когда треугольник остроугольный, прямоугольный или тупоугольный.

Доказательство: Пусть ABC - треугольник, а D, E и F - середины сторон BC, AC и AB соответственно. Предположим, что перпендикулярные биссектрисы сторон BC, AC и AB пересекаются в точке O. Тогда \(OD=OE=OF\), и, следовательно, O находится на равном расстоянии от всех трех вершин треугольника. Следовательно, \(OA=OB=OC\), и O - центр описанного круга треугольника. Если треугольник остроугольный, то центр описанного круга лежит внутри треугольника. Если треугольник прямоугольный, то центр описанного круга лежит на середине гипотенузы. Если треугольник тупоугольный, то центр описанного круга лежит вне треугольника.

Обратно, предположим, что треугольник остроугольный, прямоугольный или тупоугольный. Если треугольник остроугольный, то перпендикулярные биссектрисы сторон пересекаются внутри треугольника. Если треугольник прямоугольный, то перпендикулярные биссектрисы катетов пересекаются в середине гипотенузы. Если треугольник тупоугольный, то перпендикулярные биссектрисы сторон пересекаются за пределами треугольника. Следовательно, перпендикулярные биссектрисы сторон пересекаются тогда и только тогда, когда треугольник остроугольный, прямоугольный или тупоугольный.

Внешние круги и внешние центры:
Внешний круг треугольника - это круг, касающийся одной из его сторон и продолжений двух других сторон треугольника. Есть три внешних круга треугольника, один для каждой стороны. Центр внешнего круга называется внешним центром треугольника, соответствующим этой стороне. Внешний центр находится на биссектрисе внешнего угла у вершины, противоположной касательной стороне.

Теорема 5: Внешний центр треугольника, соответствующий данной стороне, лежит на биссектрисе внешнего угла у вершины, противоположной этой стороне.

Доказательство: Пусть ABC - треугольник, а \(I_A\) - центр внешнего круга, соответствующего стороне BC. Пусть D - точка касания внешнего круга со стороной BC, а E и F - точки касания с сторонами CA и AB соответственно. Тогда \(I_A D\) перпендикулярен BC, а \(I_A E\) и \(I_A F\) - биссектрисы углов BAC и CAB соответственно. Следовательно, \(I_A\) лежит на биссектрисе внешнего угла у вершины A. Аналогично, внешний центр \(I_B\) соответствующий стороне AC лежит на биссектрисе внешнего угла у вершины B, и внешний центр \(I_C\) соответствующий стороне AB лежит на биссектрисе внешнего угла у вершины C.

В заключение, тема о кругах, нарисованных внутри и снаружи треугольника, является важным аспектом элементарной геометрии. Теоремы, связанные с вписанными, описанными и внешними кругами, являются фундаментальными результатами, которые предоставляют ценные идеи о свойствах треугольников.

Свойства четырехугольника, вписанного и описанного около окружности ☰

Четырехугольник называется вписанным в окружность, если все его вершины лежат на окружности. Аналогично, четырехугольник называется описанным около окружности, если окружность касается всех его четырех сторон.

Свойства Четырехугольника, Вписанного в Окружность:

• Противоположные углы четырехугольника, вписанного в окружность, дополнительны. То есть сумма мер любых двух противоположных углов равна 180 градусов.
• Диагонали четырехугольника, вписанного в окружность, пересекаются под прямым углом. То есть диагонали перпендикулярны друг другу.
• Произведение длин двух диагоналей четырехугольника, вписанного в окружность, равно сумме произведений длин пар противоположных сторон. То есть, если \(ABCD\) - четырехугольник, вписанный в окружность, то \(AC \cdot BD=AB \cdot CD+AD \cdot BC\).
• Отрезки, соединяющие середины противоположных сторон четырехугольника, вписанного в окружность, пересекаются в одной точке. То есть, отрезки AC и BD пересекаются в точке P, где P - середина отрезка EF и EF - отрезок, соединяющий середины AB и CD.

Свойства Четырехугольника, Описанного около Окружности:

• Противоположные стороны четырехугольника, описанного около окружности, параллельны. То есть, $$ AB \parallel CD $$ и $$ AD \parallel BC $$
• Сумма противоположных пар сторон четырехугольника, описанного около окружности, равна диаметру окружности. $$ text{То есть, } AB+CD=AD+BC $$
• Отрезки, соединяющие точки касания окружности со сторонами четырехугольника, описанного около окружности, пересекаются в одной точке. То есть, отрезки AC и BD пересекаются в точке P, где P - пересечение касательных к окружности в точках B и D.
• Площадь четырехугольника, описанного около окружности, можно вычислить, используя формулу Брахмагупты: $$ \text{Площадь} =\sqrt{(s-a)(s-b)(s-c)(s-d)} $$ где \(a\), \(b\), \(c\) и \(d\) - длины сторон четырехугольника, а \(s\) - полупериметр, задаваемый формулой: $$ s=\frac{a+b+c+d}{2} $$
• Если четырехугольник одновременно вписан в и описан около окружности, то он должен быть квадратом. Другими словами, если четырехугольник имеет свойство, что его вершины лежат на окружности и окружность касается всех его четырех сторон, то четырехугольник должен быть квадратом.

Окружности внутри и вне правильного многоугольника ☰

Правильный многоугольник - это многоугольник, у которого все стороны и углы равны. Окружности могут быть вписаны внутрь и описаны вокруг правильного многоугольника.

Окружность, вписанная в правильный многоугольник:
Окружность, вписанная в правильный многоугольник, касается каждой стороны многоугольника в одной точке. Центр окружности также является центром многоугольника.
Пусть \(r\) - радиус вписанной окружности, \(s\) - длина стороны правильного многоугольника, а \(n\) - количество сторон многоугольника.
Площадь \(A\) правильного многоугольника можно вычислить по формуле: \( A=\frac{1}{2} nr^2 sin \frac{2 \pi }{n} \).

Периметр \(P\) правильного многоугольника определяется по формуле: \(P=ns\).
Радиус \(r\) вписанной окружности можно рассчитать по формуле: $$ r= \frac{s}{2 tan \frac{\pi}{n}} $$

Окружность, описанная вокруг правильного многоугольника:
Окружность, описанная вокруг правильного многоугольника, проходит через каждую вершину многоугольника. Центр окружности также является центром многоугольника.
Пусть \(R\) - радиус описанной окружности, \(s\) - длина стороны правильного многоугольника, а \(n\) - количество сторон многоугольника.
Площадь \(A\) правильного многоугольника можно вычислить по формуле: $$ A=\frac{1}{2} nR^2 sin \frac{2 \pi }{n} $$

Периметр \(P\) правильного многоугольника определяется по формуле: \(P = ns\).
Радиус \(R\) описанной окружности можно рассчитать по формуле: $$ R= \frac{s}{2 sin \frac{\pi}{n}} $$

Кроме того, отношение площади описанной окружности к площади вписанной окружности задается формулой: $$ \frac{\text{Площадь описанной окружности}}{ \text{Площадь вписанной окружности}} = \frac{R^2}{r^2} = \frac{sin^2 \frac{\pi}{n}}{1- sin^2 \frac{\pi}{n}} $$

Площадь многоугольника. Площадь правильного многоугольника. ☰

Площадь многоугольника - это мера двумерной области, ограниченной многоугольником. Формула для вычисления площади многоугольника зависит от его типа.
Например, площадь треугольника можно вычислить с помощью формулы: $$ \text{Площадь треугольника} = \frac{1}{2} \cdot \text{основание} \cdot \text{высота} $$

Для прямоугольника площадь можно вычислить с помощью формулы: $$ \text{Площадь прямоугольника} = \text{длина} \cdot \text{ширина} $$ Для неправильных многоугольников существуют различные методы расчета площади, такие как разделение на более простые фигуры и сложение их площадей или использование методов математического анализа.

С другой стороны, площадь правильного многоугольника можно вычислить с использованием следующей формулы: $$ \small \text{Площадь правильного многоугольника} = \frac{1}{2} \cdot \text{Периметр} \cdot \text{Апофема} $$

Где Периметр - сумма длин всех сторон многоугольника, а Апофема - перпендикулярное расстояние от центра многоугольника до одной из его сторон.

Правильный многоугольник - это многоугольник, у которого все стороны равны по длине, а все углы равны по величине. Примеры правильных многоугольников включают равносторонние треугольники, квадраты, правильные пятиугольники, шестиугольники и так далее.