Квадратные неравенства ☰

Квадратное неравенство - это тип неравенства, в котором появляется квадратичная функция. Квадратные неравенства имеют форму:
\( ax^2 + bx + c,,,,op,,,,0 \), где \(a\), \(b\) и \(c\) - действительные числа, а \(op\) - один из символов неравенства \( < \), \( \le \), \(> \) или \( \ge \).

Решение квадратного неравенства - это множество всех значений \(x\), которые удовлетворяют неравенству. Для нахождения множества решений мы можем использовать следующие шаги:

• Решите соответствующее квадратное уравнение \( ax^2 + bx + c = 0 \), чтобы найти корни квадратичной функции.
• Постройте график квадратичной функции на координатной плоскости.
• Определите область(и) графика, находящуюся над или под \(x\)-осью, в зависимости от знака \(a\).
• Затените соответствующую область(и) графика в зависимости от символа неравенства.
• Запишите множество решений, используя интервальную или множественную запись.

Давайте рассмотрим несколько примеров:
Пример 1: Решим неравенство \(x^2 - 4x + 3 \ge 0 \).
Решение: Сначала найдем корни соответствующего квадратного уравнения \(x^2 - 4x + 3 = 0 \) путем факторизации или использования квадратной формулы:
\( x^2 - 4x + 3 = (x-1)(x-3)=0 \).
Таким образом, корни - \( x=1 \) и \(x=3 \).
Затем мы строим график квадратичной функции \( f(x) = x^2 - 4x + 3 \).

График


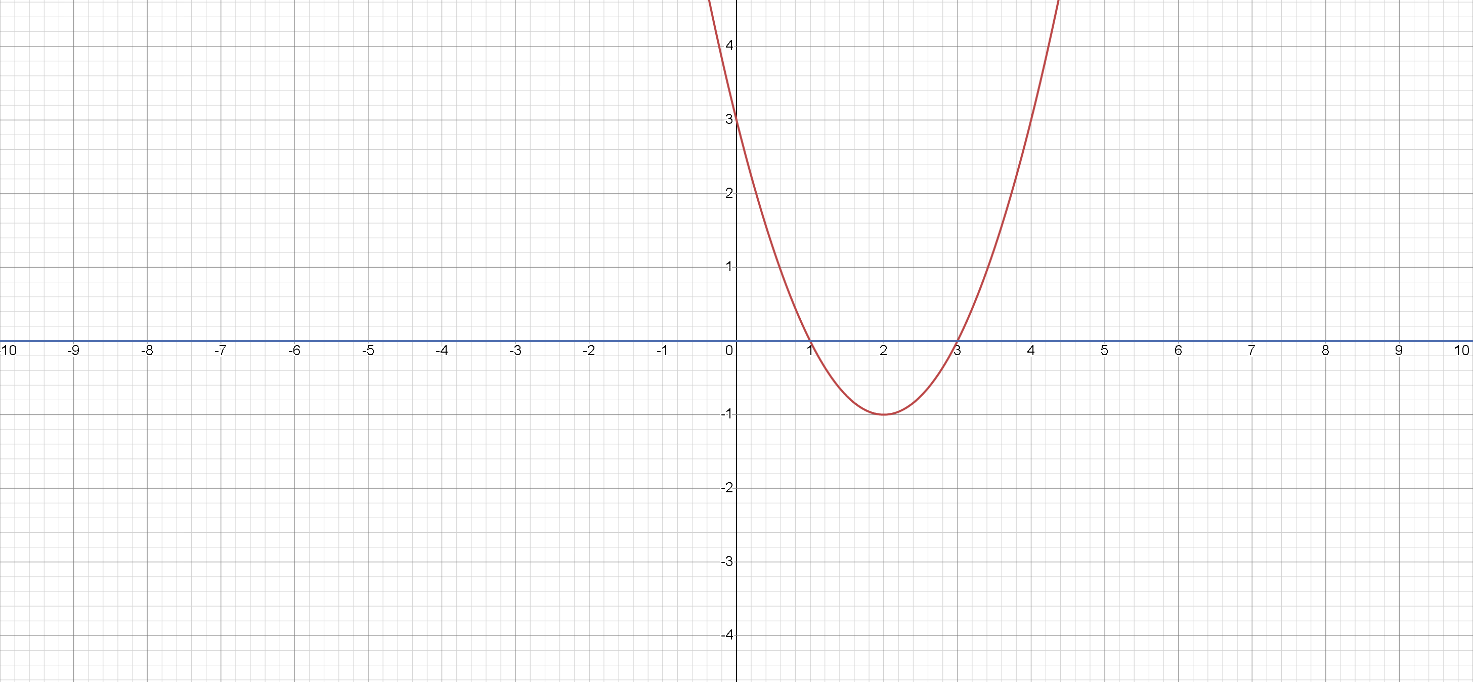
Мы видим, что график функции находится над \(x\)-осью между корнями \(x=1\) и \(x=3\).
Таким образом, решение неравенства \( x^2 - 4x + 3 \ge 0 \) это: \( x \in (-\infty, 1] \cup [3, \infty) \).

Пример 2: Пример решения квадратного неравенства методом интервалов.
Рассмотрим неравенство: \( 2x^2 - 5x - 3 < 0 \).
Чтобы решить это неравенство, сначала найдем корни квадратного уравнения \( 2x^2–5x–3=0 \)
\( x=- \frac{1}{2} \) и \( x = 3 \). Мы можем найти эти корни, факторизируя квадратное уравнение или используя квадратную формулу.
Затем мы используем корни, чтобы разделить ось чисел на три интервала:
\( (-\infty ; -\frac{1}{2} ) \), \( (-\frac{1}{2}; 3) \) и \( (3; \infty)\).
Затем мы тестируем значение из каждого интервала в неравенстве, чтобы определить, верно оно или ложно в этом интервале.

Для интервала \( (-\infty ; -\frac{1}{2}) \) мы можем выбрать \( x= -1 \) в качестве тестового значения.
Подставив \(x=-1\) в неравенство, мы получим: \( 2(-1)^2 - 5(-1) - 3 < 0 \), что упрощается до: \( 4 < 0 \).
Это ложное утверждение, поэтому неравенство не выполняется в интервале \( (-\infty ; -\frac{1}{2}) \) .

Для интервала \( (-\frac{1}{2} ; 3) \) мы можем выбрать \(x=0\) в качестве тестового значения.
Подставив \(x=0\) в неравенство, мы получим: \( 2(0)^2 - 5(0) - 3 < 0 \), что упрощается до: \( -3 < 0 \).
Это верное утверждение, поэтому неравенство выполняется в интервале \( (-\frac{1}{2} ; 3) \).

Для интервала \( (3; \infty) \) мы можем выбрать \(x=4\) в качестве тестового значения.
Подставив \(x=4\) в неравенство, мы получим: \(2(4)^2 - 5(4) - 3 < 0 \), что упрощается до: \( 5 < 0 \) .
Это ложное утверждение, поэтому неравенство не выполняется в интервале \( (3;\infty) \).

Таким образом, решение неравенства \( 2x^2–5x–3 < 0 \) это: \( x\ \in (-\frac{1}{2} ; 3) \)
Это означает, что любое значение \(x\), которое больше \(-\frac{1}{2} \) и меньше \(3\), делает неравенство истинным.

Решение рациональных неравенств методом интервалов ☰

Для решения рациональных неравенств методом интервалов следуйте этим шагам:

• Перепишите неравенство в виде одного рационального выражения, с нулем на одной стороне и другой стороной в одной дроби.
• Определите критические значения выражения, найдя места, где числитель и знаменатель равны нулю.
• Разделите число на интервалы, разделенные критическими значениями, найденными на шаге 2.
• Определите знак выражения в каждом интервале и определите интервалы, в которых выражение положительно или отрицательно.
• Запишите решение в интервальной записи, используя интервалы, в которых выражение положительно или отрицательно, в зависимости от направления неравенства.

Например, давайте решим неравенство \(\frac{2x-5}{x+1} > 1 \) методом интервалов.
1. Перепишем неравенство в виде одного рационального выражения:
\(\frac{2x-5}{x+1} -1 > 0 \)

Упростим левую часть и объединим подобные члены:
\( \frac{2x-5-(x+1)}{x+1} > 0 \)

\( \frac{x-6}{x+1} \)


2. Определим критические значения, установив числитель и знаменатель равными нулю:
\( x-6=0 \rightarrow x=6 \).
\( x+1=0 \rightarrow x=-1 \).


3. Разделим число на интервалы:
\( (-\infty ; -1) \), \( (-1;6) \), \( (6;\infty ) \).


4. Определим знак выражения в каждом интервале, проверив точку в каждом интервале:
Для \( x=-2 \), \( \frac{-2-6}{-2+1} = 8 > 0 \) , поэтому выражение положительно в \( (-\infty ; -1) \).

Для \( x = 0 \), \( \frac{0-6}{0+1} = -6 < 0 \) , поэтому выражение отрицательно в \( (-1 ; 6 ) \).

Для \( x = 7 \), \( \frac{7-6}{7+1} = \frac{1}{8} > 0 \) , поэтому выражение положительно в \( (6; \infty ) \).


5. Запишите решение в интервальной записи:
Неравенство верно там, где выражение положительно, поэтому решение - \( x \in (- \infty ; -1 ) \cup (6; \infty ) \).

Неравенства с иррациональными выражениями ☰

Иррациональное неравенство - это неравенство, включающее одно или несколько иррациональных выражений, таких как квадратные корни или кубические корни. Процесс решения иррационального неравенства отличается от процесса решения обычного неравенства, потому что возведение в квадрат или в степень может привести к появлению лишних решений. Для решения иррационального неравенства необходимо изолировать иррациональное выражение на одной стороне неравенства, а затем возвести обе стороны неравенства в квадрат или возвести их в степень, которая устраняет корень. Однако при этом может возникнуть решения, которые не являются допустимыми для исходного неравенства, потому что возведение в квадрат или в степень может изменить знак числа. Поэтому необходимо проверить свои решения, чтобы убедиться, что они действительно подходят для исходного неравенства.

Для решения иррациональных неравенств следуйте этим общим шагам:
1. Изолируйте иррациональное выражение на одной стороне неравенства.

2. Возведите в квадрат обе стороны неравенства (или возведите обе стороны в степень, которая устраняет корень).

3. Решите полученное неравенство.

4. Проверьте решения исходного неравенства, поскольку возведение в квадрат или в степень может привести к появлению лишних решений.


Например, давайте решим неравенство \( \sqrt{2x-1} > 3 \) .

1. Возведем в квадрат обе стороны неравенства:
\( (\sqrt{2x-1})^2 > 3^2 \rightarrow 2x - 1 > 9 \)

2. Решим полученное неравенство:
\( 2x > 10 \rightarrow x > 5 \) .
\( \small \sqrt{2x-1} > 3 \rightarrow 2x > 10 \rightarrow x > 5 \)

3. Проверим решение исходного неравенства:
Подставим \(x=6\) в исходное неравенство:
\( \sqrt{2(6)-1} > 3 \rightarrow \sqrt{11} > 3 \)
Это верно, поэтому \(x=6\) является допустимым решением неравенства.

Подставим \(x=4\) в исходное неравенство:
\( \sqrt{2(4)-1} > 3 \rightarrow \sqrt{7} > 3 \)
Это неверно, поэтому \(x=4\) не является допустимым решением неравенства.
Следовательно, решение - \(x > 5\).

Примечание: Всегда обратите внимание, что под корнем не может быть отрицательное число.