Тела Вращения в Геометрии: Полное руководство по сферам, конусам и цилиндрам

Введение в Тела Вращения

Классификация Тел Вращения

Выпуклые тела: Тела, в которых любой отрезок, соединяющий две точки внутри тела, полностью лежит внутри тела. Примеры включают сферы, конусы и цилиндры.
Невыпуклые тела: Тела, в которых некоторые отрезки, соединяющие внутренние точки, могут частично лежать вне тела. Примеры включают торы и вогнутые многогранники.

Основные теоремы

Теорема Паппа о центроиде: Утверждает, что объем тела вращения равен произведению площади образующей фигуры и длины пути вращения её центроида.
Принцип Кавальери: Если два тела имеют равные высоты и равные площади поперечного сечения на каждой высоте, их объемы равны.

Свойства сферической геометрии

Параллельные линии: Отсутствуют в сферической геометрии
Углы треугольника: Сумма превышает 180 градусов
Вычисление площади: Пропорционально избыточному углу

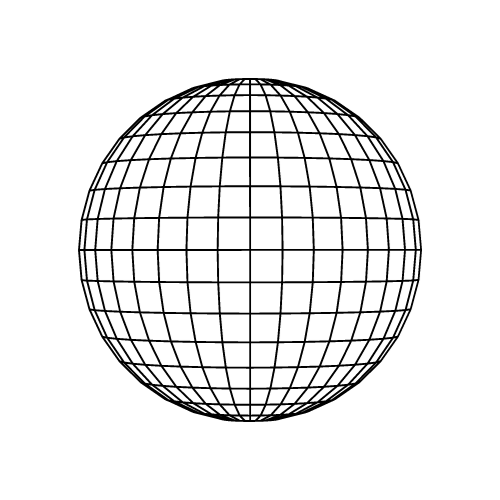
Сфера

Совершенно симметричное тело, в котором все точки поверхности равноудалены от центра.

Сфера

Основные формулы

Площадь поверхности: $SA = 4\pi r^2$
Объем: $V = \frac{4}{3}\pi r^3$
Диаметр: $D = 2r$

Свойства

Равное расстояние от центра до всех точек поверхности
Минимальная площадь поверхности для заданного объема
Бесконечное количество осей симметрии
Оптимальное соотношение объема к площади поверхности

Применение в реальном мире

Небесные тела: Гравитационные силы создают приблизительно сферические планеты
Капли жидкости: Поверхностное натяжение формирует сферические формы
Сосуды под давлением: Сферические резервуары для оптимального распределения давления

Конус

Тело, образованное соединением всех точек плоского основания с одной вершиной.

Конус

Основные формулы

Площадь боковой поверхности: $S_{LSA} = \pi rl$
Общая площадь поверхности: $S_{SA} = \pi r(r+l)$
Объем: $V = \frac{1}{3}\pi r^2h$
Высота наклона: $l = \sqrt{r^2 + h^2}$

Усеченный конус

Часть конуса, образованная параллельными срезами основания.

V = \frac{1}{3}\pi h(R^2 + r^2 + Rr)

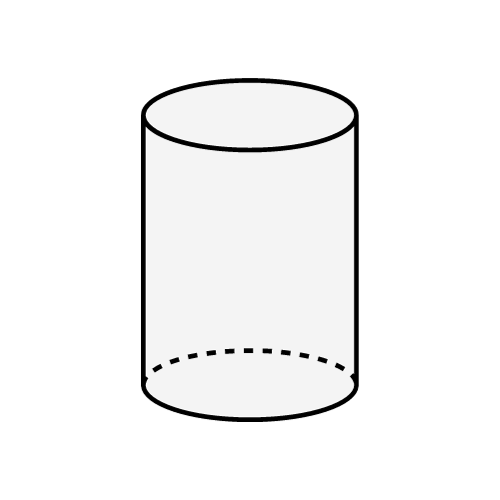
Цилиндр

Тело с параллельными, конгруэнтными основаниями, соединенными криволинейной поверхностью.

Цилиндр

Основные формулы

Площадь поверхности: $SA = 2\pi r^2 + 2\pi rh$
Площадь боковой поверхности: $LSA = 2\pi rh$
Объем: $V = \pi r^2h$

Типы цилиндров

Прямой круговой цилиндр: Круглое основание с перпендикулярной осью
Эллиптический цилиндр: Эллиптическое основание с формулой объема: $V = \pi abh$

Применение

Инженерия: Трубы, колонны, резервуары для хранения
Оптика: Цилиндрические линзы для коррекции астигматизма
Архитектура: Конструкционные опоры и декоративные элементы