Угол поворота
Угол поворота - это концепция, используемая в геометрии для описания количества поворота, применяемого к фигуре вокруг фиксированной точки, называемой центром вращения. Когда фигура поворачивается, все точки на фигуре перемещаются по круговым путям вокруг центра вращения, а угол поворота - это количество поворота, измеренное в градусах или радианах, которое фигура
проходит.
Для математического определения угла поворота нам нужно использовать концепцию единичной окружности. Единичная окружность - это окружность, центрированная в начале координат плоскости декартовых координат с радиусом 1. Мы можем использовать единичную окружность для определения синуса и косинуса угла, которые являются фундаментальными тригонометрическими функциями.
Предположим, у нас есть точка \((x,y)\) на единичной окружности, которая образует угол \( \theta \) с положительной осью \(x\), как показано на рисунке ниже:
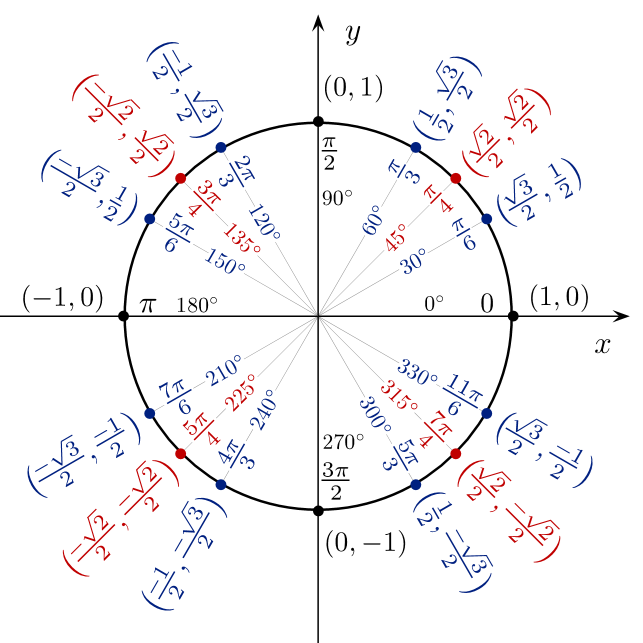
Тогда координаты точки задаются:
\( x = \cos( \theta ) \), \( y = \sin( \theta) \).
Угол поворота можно определить следующим образом. Предположим, у нас есть фигура \(F\) на плоскости, и мы вращаем фигуру против часовой стрелки вокруг фиксированной точки \(O\) на угол \( \theta \). Пусть \(F' \) будет образом \(F\) при этом вращении. Тогда угол поворота определяется как угол между любыми двумя соответствующими отрезками прямых \(F \) и \(F' \),
которые пересекаются в центре вращения \(O\).
Мы можем выразить угол поворота через координаты точек на единичной окружности. Предположим, у нас есть точка \(P=(x,y) \) на \(F\), которая вращается против часовой стрелки вокруг \(O\) на угол \( \theta \), и пусть \( P'=(x',y' ) \) будет соответствующей точкой на \(F' \). Тогда угол поворота можно вычислить с использованием следующей формулы:
\( \theta = \cos^{-1}\left(\frac{xx' + yy'}{\sqrt{x^2 + y^2} \sqrt{{x'}^2 + {y'}^2}}\right) \)
Эта формула выводится из формулы скалярного произведения для угла между двумя векторами. Числитель дроби представляет собой скалярное произведение векторов \(OP\) и \(OP'\), а знаменатель - произведение их модулей.
В заключение, угол поворота - это мера количества поворота, применяемого к фигуре вокруг фиксированной точки, и его можно вычислить с использованием формулы скалярного произведения или измеряя угол между соответствующими отрезками прямых исходной и повернутой фигур.
Градус и радиан
Угол - это геометрическая фигура, образованная двумя лучами или отрезками прямой, которые имеют общую точку, называемую вершиной. Углы могут измеряться в различных единицах, но наиболее распространенными единицами являются радианы и градусы.
Радианы - это единица измерения угла, основанная на длине дуги окружности. Один радиан определяется как угол, который описывает дугу длиной, равной радиусу окружности. Другими словами, если окружность имеет радиус \(r\), то угол в один радиан в центре окружности охватывает дугу длиной \(r\). Символ для радианов - "rad".
Градусы - это еще одна единица измерения угла, основанная на делении окружности на 360 равных частей, каждая часть составляет один градус. Символ для градусов - "\( \circ \)". Одно полное вращение вокруг окружности эквивалентно 360 градусам \( (360^\circ ) \).
Для преобразования между радианами и градусами можно использовать следующие формулы:
- Для преобразования из радиан в градусы: умножьте угол на \( \frac{180}{\pi} \).
- Для преобразования из градусов в радианы: умножьте угол на \( \frac{\pi}{180} \).
Например, предположим, у нас есть угол \( \theta = 2 \text{ радиана}\). Чтобы преобразовать этот угол в градусы, мы можем использовать формулу:
\( \theta = \text{радиана} \cdot \frac{180}{\pi} = 2 \cdot \frac{180}{\pi} \approx 114.59^\circ \)
Аналогично, предположим, у нас есть угол \( \theta = 45^\circ \). Чтобы преобразовать этот угол в радианы, мы можем использовать формулу:
\( \theta = \text{градусы} \cdot \frac{\pi}{180} = 45 \cdot \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ рад} \)
В заключение, радианы и градусы - две распространенные единицы измерения угла, используемые для измерения углов в геометрии. Радианы основаны на длине дуги окружности, а градусы - на делении окружности на 360 равных частей. Мы можем преобразовывать радианы в градусы и наоборот, используя упомянутые выше формулы.
Тригонометрические функции и единичная окружность
Тригонометрические функции - это математические функции, которые связывают углы треугольника с длинами его сторон. Самые часто используемые тригонометрические функции - синус, косинус и тангенс. Эти функции часто представляются с использованием единичной окружности, которая представляет собой окружность с радиусом 1, центрированную в начале координат декартовой
системы координат.
Единичная окружность полезна, потому что она позволяет нам легко визуализировать отношения между углами и тригонометрическими функциями. Если мы проведем линию от начала координат до точки на единичной окружности, угол между этой линией и положительным направлением оси x называется углом поворота или просто углом. Точка, где линия пересекает единичную окружность,
соответствует определенному значению синуса, косинуса и тангенса.
Вот определения трех основных тригонометрических функций:
- Синус (sin): отношение длины стороны, противолежащей углу, к длине гипотенузы прямоугольного треугольника.
- Косинус (cos): отношение длины стороны, прилегающей к углу, к длине гипотенузы прямоугольного треугольника.
- Тангенс (tan): отношение длины стороны, противолежащей углу, к длине стороны, прилегающей к углу, прямоугольного треугольника.
С использованием единичной окружности мы также можем определить еще три тригонометрические функции: косекант (csc), секант (sec) и котангенс (cot). Это просто обратные значения синуса, косинуса и тангенса, соответственно.
Функции синуса, тангенса, котангенса являются нечетными, а косинус - четной функцией.
Тригонометрические функции любого угла
Тригонометрические функции могут быть определены для любого угла, а не только для углов в прямоугольных треугольниках. Определения тригонометрических функций угла в единичной окружности приведены ниже:
Рассмотрим угол \( \theta \) в стандартном положении, то есть он начинается с положительной оси \(x\) и поворачивается против часовой стрелки.
Пусть \((x,y)\) - точка, где терминальная сторона угла \( \theta \) пересекает единичную окружность с центром в начале координат.
Синус (sin): \( sin(\theta ) = y \)
Косинус (cos): \( cos( \theta ) = x \)
Тангенс (tan): \( tan( \theta ) = \frac{y}{x} \), \(x \neq 0 \)
Другие тригонометрические функции могут быть определены следующим образом:
Косекант (csc): \( csc( \theta ) = \frac{1}{sin \theta } \)
Секант (sec): \( sec(\theta ) = \frac{1}{cos \theta } \)
Котангенс (cot): \( cot(\theta ) = \frac{1}{tan \theta } \)
Значения тригонометрических функций могут быть положительными, отрицательными или нулевыми, в зависимости от квадранта, в котором находится угол \( \theta \). В первом квадранте \( ( 0 < \theta < 90 \text{ градусов}) \) все шесть тригонометрических функций положительны. Во втором квадранте \( ( 90 < \theta < 180 \text{ градусов}) \) только синус положителен. В
третьем квадранте \( ( 180 < \theta < 270 \text{ градусов}) \) только тангенс положителен. В четвертом квадранте \( ( 270 < \theta < 360 \text{ градусов}) \) только косинус положителен.
Имейте в виду, что углы могут быть измерены в градусах или радианах. Радианы - это еще один способ измерения углов, где один радиан определяется как угол, который занимает дугу длиной равной радиусу круга. Конверсия между градусами и радианами задается следующим образом:
\( \pi \text{ радиан} = 180 \text{ градусов} \)
\( \text{1 радиан } \approx 57.3 \text{ градусов} \)
\( \text{1 градус } \approx 0.0175 \text{ радиан} \)
При работе с тригонометрическими функциями углов, измеренных в радианах, мы используем греческую букву \( \pi \) (пи) как удобный способ выражения этих углов. Например, угол 90 градусов можно выразить как \( \frac{\pi}{2}\) радиан, а угол 180 градусов можно выразить как \( \pi \) радиан.
Мы также можем использовать тригонометрические тождества для упрощения тригонометрических выражений. Например, тождество Пифагора утверждает, что \( sin^2 (\theta)+cos^2 (\theta)=1 \), что верно для всех значений \( \theta \). Еще одно полезное тождество - это обратное тождество, которое связывает тригонометрические функции со своими обратными значениями:
\( \csc(\theta) = \frac{1}{\sin(\theta)} \)
\( \sec(\theta) = \frac{1}{\cos(\theta)} \)
\( \cot(\theta) = \frac{1}{\tan(\theta)} \)
Существует множество других тригонометрических тождеств, которые можно использовать для упрощения тригонометрических выражений или решения тригонометрических уравнений.
В целом, тригонометрические функции любого угла являются важным понятием в математике и имеют широкий спектр применений в таких областях, как физика, инженерия и геометрия.
Формула поворота
Формулы поворота - это набор уравнений, используемых для вычисления новых координат точки после ее поворота на заданный угол вокруг фиксированной точки в координатной системе. Существует несколько вариаций этих формул в зависимости от конкретной задачи, но я объясню основную идею за ними.
Предположим, у нас есть точка \(P\) в координатной системе, с координатами \((x,y)\). Мы хотим повернуть эту точку вокруг фиксированной точки \(O\) (называемой центром поворота) на угол \( \theta \). Цель - найти новые координаты \((x',y' ) \) \(P\) после этого поворота.
Для этого мы используем набор уравнений, связывающих новые координаты с исходными координатами и углом поворота. Один из способов получить эти уравнения - использовать базовую тригонометрию. Мы можем рассмотреть треугольник, образованный центром поворота \(O\), исходной точкой \(P\) и повернутой точкой \(P'\). Стороны этого треугольника имеют длины \(x\), \(y\) и
\(r\) (расстояние от \(O\) до \(P\)), а угол между \(x\)-осью и линией \(OP\) равен \( \varphi \). После поворота угол между \(x\)-осью и линией \(OP'\) равен \( \varphi +\theta \).
Используя тригонометрию, мы можем выразить новые координаты \((x',y' ) \) через исходные координаты \((x,y)\) и угол поворота \(\theta \) следующим образом:
\( x' = xcos(\theta ) - ysin( \theta ) \)
\( y' = xsin( \theta ) + ycos( \theta ) \)
Эти уравнения дают нам новые координаты \(P'\) после поворота \(P\) на угол \( \theta \) вокруг \(O\).
Чтобы понять, почему эти уравнения работают, рассмотрим первое уравнение. Косинус \( \theta \) представляет изменение \(x\)-координаты \(P\) после поворота на \( \theta \), а синус \( \theta \) представляет изменение \(y\)-координаты. Следовательно, \( xcos( \theta ) \) представляет новую \(x\)-координату \(P'\), полученную поворотом исходной \(x\)-координаты \(P\),
а \(ysin(\theta ) \) представляет новую \(y\)-координату, полученную поворотом исходной \(y\)-координаты. Вычитая эти величины, мы получаем новую \(x\)-координату \(P'\) относительно \(x\)-оси. Аналогично второе уравнение дает нам новую \(y\)-координату \(P'\) относительно \(y\)-оси.
Существует несколько вариаций формул поворота, которые используются в различных контекстах. Вот несколько примеров:
Поворот вокруг точки, отличной от начала координаты:
Базовые формулы поворота предполагают, что точка \(P\) вращается вокруг начала координаты. Если мы хотим повернуть точку относительно другой точки \(Q\), мы можем сначала перевести систему координат так, чтобы \(Q\) стал началом координаты, затем применить базовые формулы и, наконец, перевести систему координат обратно. Также можно использовать более общую форму
формул поворота, учитывающую координаты точки \(Q\). Например, если мы хотим повернуть точку \(P\) на угол \( \theta \) относительно точки \(Q\) с координатами \((a,b)\), новые координаты \((x',y') \) могут быть вычислены следующим образом:
\( x' = (x-a) \cdot cos(\theta ) - (y-b) \cdot sin(\theta ) + a \)
\( y' = (x-a) \cdot sin(\theta ) + (y-b) \cdot cos(\cdot ) + b \)
Поворот комплексных чисел:
В комплексном анализе комплексное число \(z\) может быть представлено как \(z=x+yi\), где \(x\) и \(y\) - действительная и мнимая части соответственно. Поворот плоскости комплексных чисел может быть представлен умножением комплексного числа \(z\) на комплексное число вида \(w=cos(\theta )+isin(\theta ) \), где \(\theta \) - угол поворота. Полученное комплексное
число \(z'=wz\) имеет эффект поворота \(z\) против часовой стрелки вокруг начала координаты на угол \( \theta\).
В заключение, формулы поворота - это фундаментальный инструмент в геометрии и физике, который позволяет нам преобразовывать точки и объекты, поворачивая их вокруг фиксированной точки или оси. Они могут быть выражены в различных формах в зависимости от задачи и используются в широком спектре приложений.
Самые распространенные углы поворота - \( 90^\circ \), \( 180^\circ \) и \(270^\circ \).
| Тип поворота | Точка на изображении | Точка на изображении после поворота |
|---|---|---|
| \(90^\circ \) по часовой стрелке. | \((x,y) \) | \( (y,-x) \) |
| \( 90^\circ \) против часовой стрелки | \( (x,y) \) | \( (-y,x) \) |
| \( 180^\circ \) по часовой стрелке. | \( (x,y) \) | \( (-x,-y) \) |
| \( 180^\circ \) против часовой стрелки | \( (x,y) \) | \( (-x,-y) \) |
| \( 270^\circ \) по часовой стрелке. | \( (x,y) \) | \( (-y,x) \) |
| \( 270^\circ \) против часовой стрелки | \( (x,y) \) | \( (y,-x) \) |
Обратите внимание, что в таблице точка \((x,y) \) представляет собой координаты точки на исходном изображении до поворота, а точка в третьем столбце представляет собой координаты той же точки после поворота. Угол поворота измеряется в градусах, а направления "по часовой стрелке" и "против часовой стрелки" относятся к направлению вращения вокруг начала координаты.
Тригонометрические тождества
Тригонометрические тождества - это математические уравнения, которые связывают тригонометрические функции (синус, косинус, тангенс и т. д.) и верны для всех возможных значений переменных, вовлеченных в них. Эти тождества широко используются в тригонометрии и математическом анализе для упрощения и манипулирования выражениями, содержащими тригонометрические функции.
Вот некоторые из самых важных тригонометрических тождеств:
Пифагорово тождество:
\( sin^2 (x) + cos^2 (x) = 1 \)
Это тождество связывает синус и косинус и выражает тот факт, что сумма их квадратов всегда равна единице. Оно происходит из теоремы Пифагора в геометрии, которая утверждает, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы.
Реципрочные тождества:
\( sin(x) = \frac{1}{csc(x)} \)
\( cos(x) = \frac{1}{sec(x)} \)
\( tan(x) = \frac{1}{cot(x)} \)
Эти тождества выражают обратные отношения между тригонометрическими функциями и их соответствующими обратными функциями (косеканс, секанс и котангенс). Например, первое тождество утверждает, что синус угла равен обратному к косекансу этого угла.
Четно-нечетные тождества:
\( sin(-x) = -sin(x) \)
\( cos(-x) = cos(x) \)
Эти тождества выражают четно-нечетную симметрию функций синуса и косинуса. Они утверждают, что функция синуса является нечетной функцией (т.е. меняет знак при отрицании угла), в то время как функция косинуса является четной функцией (т.е. остается неизменной при отрицании угла).
Тождества для суммы и разности:
\( sin(x+y) = sin(x) cos(y) + cos(x)sin(y) \)
\( sin(x-y) = sin(x) cos(y) - cos(x)sin(y) \)
\( cos(x+y) = cos(x) cos(y) - sin(x)sin(y) \)
\( cos(x-y) = cos(x) cos(y) + sin(x)sin(y) \)
Эти тождества выражают тригонометрические функции суммы и разности двух углов через тригонометрические функции отдельных углов. Они широко используются в математическом анализе и других разделах математики для упрощения выражений, содержащих тригонометрические функции.
Тождества двойного угла:
\( sin (2x) = 2 sin (x) cos (x) \)
\( cos(2x) = cos^2 (x) - sin^2 (x) = \) \(2cos^2 (x) - 1 = 1-2 sin^2 (x) \)
Эти тождества выражают тригонометрические функции удвоенного угла через тригонометрические функции самого угла. Они широко используются в математическом анализе и других разделах математики для упрощения выражений, содержащих тригонометрические функции.
Тождества половинного угла:
\( sin( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{2} } \)
\( cos( \frac{x}{2} ) = \pm \sqrt{ \frac{1+ cos x}{2} } \)
\( tan( \frac{x}{2} ) = \pm \sqrt{ \frac{1- cos x}{1+ cos x} } \)
Эти тождества выражают тригонометрические функции половины угла через тригонометрические функции самого угла. Они широко используются в математическом анализе и других разделах математики для упрощения выражений, содержащих тригонометрические функции.
Тождества произведения-суммы:
\( sin(x)sin(y) = \frac{1}{2} [cos(x-y) - cos(x+y) ] \)
\( cos(x) cos(y) = \frac{1}{2} [cos(x-y) + cos(x+y) ] \)
\( sin(x) cos(y) = \frac{1}{2} [sin(x+y) + sin(x-y) ] \)
Эти тождества выражают произведение двух тригонометрических функций в виде суммы или разности тригонометрических функций. Они используются для упрощения произведений, содержащих тригонометрические функции.
Тождества суммы-произведения:
\( sin(x) + sin(y) = 2 sin [ \frac{x+y}{2} ] cos [ \frac{x-y}{2} ] \)
\( sin (x) - sin (y) = 2 cos [ \frac{x+y}{2} ] sin [ \frac{x-y}{2} ] \)
\( cos(x) + cos(y) = 2 cos[ \frac{x+y}{2} ] cos[ \frac{x-y}{2} ] \)
\( cos(x)-cos(y) = -2sin[ \frac{x+y}{2} ] sin[ \frac{x-y}{2} ] \)
Эти тождества выражают сумму или разность двух тригонометрических функций в виде произведения тригонометрических функций. Они используются для упрощения сумм или разностей, содержащих тригонометрические функции.
Тождества кофункций:
\( sin(x) = cos( 90^\circ - x) \)
\( cos(x) = sin( 90^\circ - x) \)
\( tan(x) = ctg( 90^\circ - x) \)
\( ctg(x) = tan( 90^\circ - x) \)
Эти тождества выражают отношение между тригонометрической функцией и ее кофункцией (т.е. функцией комплементарного угла). Они используются для упрощения выражений, содержащих комплементарные углы.
Тождества периодичности:
\( sin(x + 2 \pi) = sin(x) \)
\( cos(x + 2 \pi ) = cos(x) \)
\( tan(x + \pi ) = tan(x) \)
Эти тождества выражают периодическую природу тригонометрических функций. Они утверждают, что синус и косинус функции повторяются каждые \(2 \pi \) радиан, в то время как тангенс функции повторяется каждые \( \pi \) радиан.
Это некоторые из наиболее важных тригонометрических тождеств, используемых в математике. Запоминая эти тождества и понимая, как их применять, студенты могут стать опытными в тригонометрии и решать сложные задачи, связанные с тригонометрическими функциями.
Упрощение тригонометрических выражений
Тригонометрические функции являются важной частью математики и физики, и упрощение тригонометрических выражений - важное умение для решения уравнений и доказательства тождеств. Упрощение тригонометрических выражений включает их алгебраическое преобразование до тех пор, пока они не будут в более простой форме, с которой легче работать.
Самые распространенные тригонометрические функции - синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти функции могут быть определены как отношения сторон прямоугольного треугольника или как функции на единичной окружности.
Для упрощения тригонометрического выражения необходимо использовать различные тригонометрические тождества и свойства. Некоторые из наиболее часто используемых тождеств включают:
Пифагоровы тождества:
\( \sin^2(\theta) + \cos^2(\theta) = 1 \)
\( \tan^2(\theta) + 1 = \sec^2(\theta) \)
\( 1 + \cot^2(\theta) = \csc^2(\theta) \)
Тождества для суммы и разности углов:
\( \sin(\alpha \pm \beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta) \)
\( \cos(\alpha \pm \beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta) \)
\( \tan(\alpha \pm \beta) = \frac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha)\tan(\beta)} \)
Тождества для удвоенного угла:
\( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \)
\( \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) \)
\( \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \)
Тождества для половинного угла:
\( \sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}} \)
\( \cos\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 + \cos(\theta)}{2}} \)
\( \tan\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}} \)
Используя эти тождества, можно упрощать тригонометрическое выражение шаг за шагом до его простейшей формы. Некоторые примеры упрощения тригонометрических выражений:
\( sin^2 (x)+cos^2 (x) \rightarrow 1 \)
\( \frac{sin^2 (x)}{1-cos(x)} \rightarrow \frac{1+cos(x)}{2-cos(x)} \)
\( \frac{sin(x)}{cos(x)} - \frac{cos(x)}{sin(x)} \rightarrow \frac{sin^2 (x)-cos^2 (x)}{sin(x)cos(x)} \)
\( \frac{sin(x)}{cos(x) +1} + \frac{1}{cos(x)-1} \rightarrow \frac{2sin(x)}{cos^2 (x)-1} \)
Важно отметить, что при упрощении тригонометрических выражений следует обращать внимание на область значений выражения. Некоторые тригонометрические функции не определены для определенных значений угла, таких как \(tan(\theta )\) и \(cot(\theta ) \) для \( \theta = \frac{\pi}{2} +k \pi \) где \(k\) - целое число. Кроме того, некоторые тождества справедливы только
для определенных значений угла или при выполнении определенных условий, например, тождества для половинного угла справедливы только для \( \frac{\pi}{2} \le \theta \le \pi \) и \(cos(\theta ) \le 0 \).
В заключение, упрощение тригонометрических выражений включает использование различных тождеств и свойств для их алгебраического преобразования до простейшей формы. Необходимо обращать внимание на область значений выражения и убедиться, что используемые тождества справедливы для заданных значений угла.