Периодические функции. Периодичность тригонометрических функций. ☰

Периодические функции - это функции, которые повторяют свои значения с регулярными интервалами или периодами. Концепция периодичности важна в различных областях математики, таких как анализ Фурье и обработка сигналов. Функция \(f(x)\) считается периодической, если существует ненулевая константа \(P\), такая что для всех \(x\) в области определения \(f\) выполняется следующее условие:
\(f(x+P)=f(x)\).

Самое маленькое положительное значение \(P\), для которого выполняется это условие, называется периодом функции.

Тригонометрические функции, такие как синус и косинус, являются фундаментальными примерами периодических функций. Давайте обсудим периодичность функций синуса и косинуса:

Функция синуса: Функция синуса, обозначаемая \( sin(x) \), периодична с периодом \( 2 \pi \). Это означает, что для всех \(x\):
\( sin(x+2 \pi )=sin(x) \).

Другими словами, функция синуса повторяет свои значения каждые \( 2 \pi \) единиц вдоль оси \(x\).

Функция косинуса: Функция косинуса, обозначаемая \(cos(x) \), также периодична с периодом \( 2 \pi \). Это означает, что для всех \(x\):
\( cos(x+ 2 \pi )=cos(x) \).

Как и функция синуса, функция косинуса также повторяет свои значения каждые \( 2 \pi \) единиц вдоль оси \(x\).

Функция тангенса, обозначаемая \( tan(x) \), является еще одним примером периодической тригонометрической функции. Однако ее период отличается от синуса и косинуса. Функция тангенса имеет период \( \pi \), что означает, что для всех \(x\):
\( tan(x+ \pi )=tan(x) \).

Функция тангенса повторяет свои значения каждые \( \pi\) единиц вдоль оси \(x\).

В заключение, тригонометрические функции являются периодическими функциями, причем функции синуса и косинуса имеют период \( 2 \pi \), а функция тангенса - период \( \pi \). Эти периодические свойства являются ключевыми при решении тригонометрических уравнений и анализе периодических явлений в различных научных и инженерных приложениях.

Графики функций синуса и косинуса ☰

Графики функций синуса и косинуса, \( y=\sin(x) \) и \(y=\cos(x) \), являются ключевыми для понимания их свойств и поведения. Обе функции периодичны и осциллируют между \(-1\) и \(1\). Графики демонстрируют периодичность и амплитуду этих функций. Давайте подробно обсудим графики обеих функций.

График \( y=\sin(x) \) :
Функция синуса имеет период \( 2 \pi \). Это означает, что она повторяет свои значения каждые \( 2 \pi \) единиц вдоль оси \(x\). График функции синуса начинается в начале координат \((0,0)\) и осциллирует между \(-1\) и \(1\) с некоторыми ключевыми точками:
\( x = \frac{ \pi }{2} \), \( \sin(x)=1 \) (максимальное значение)
\( x = \pi \), \( \sin(x) = 0 \) (пересечение нуля)
\( x= \frac{3 \pi }{2} \), \( \sin(x)= -1 \) (минимальное значение)
\(x=2 \pi \), \( \sin(x)=0 \) (пересечение нуля и один полный цикл)

Функция синуса имеет волновую форму, и ее график симметричен относительно начала координат (нечетная функция). График расширяется бесконечно в обе стороны оси \(x\), повторяя свой узор каждые \(2 \pi \) единицы.


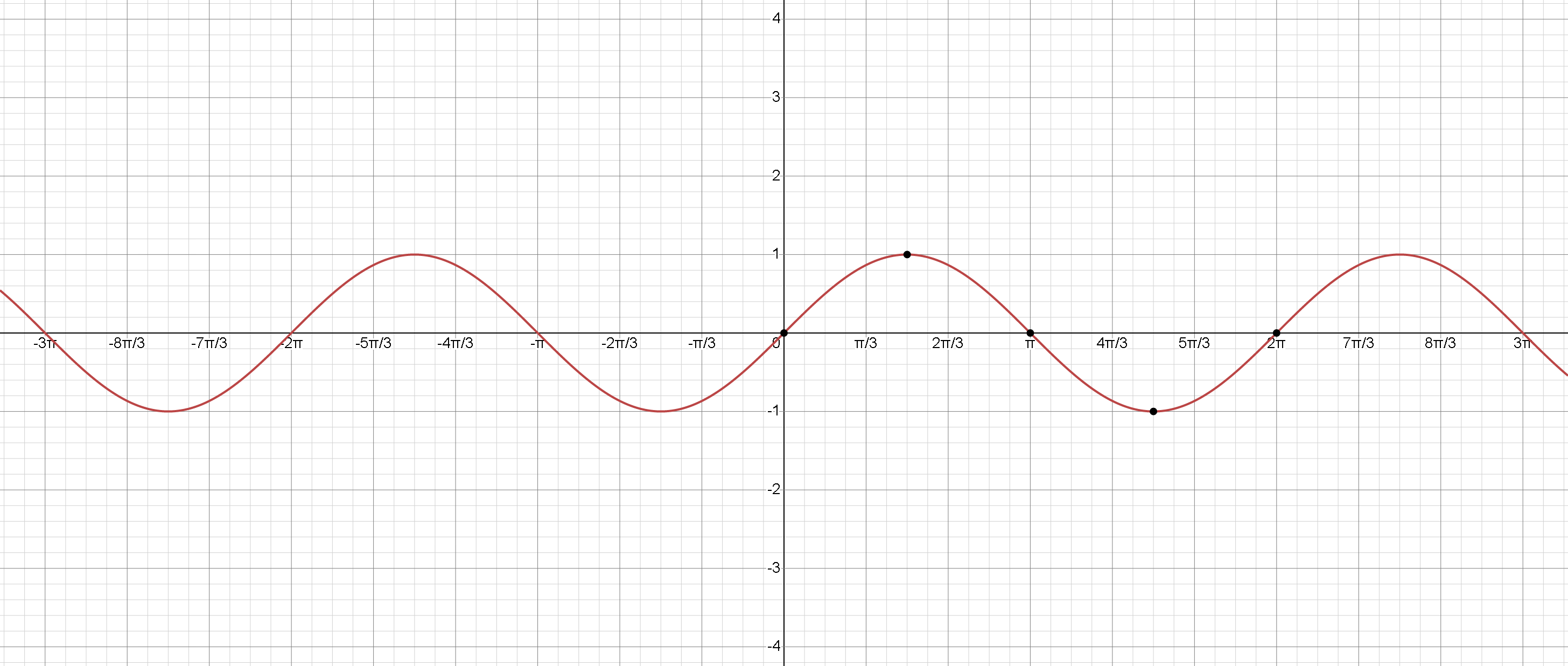
График \( y=\cos(x) \):
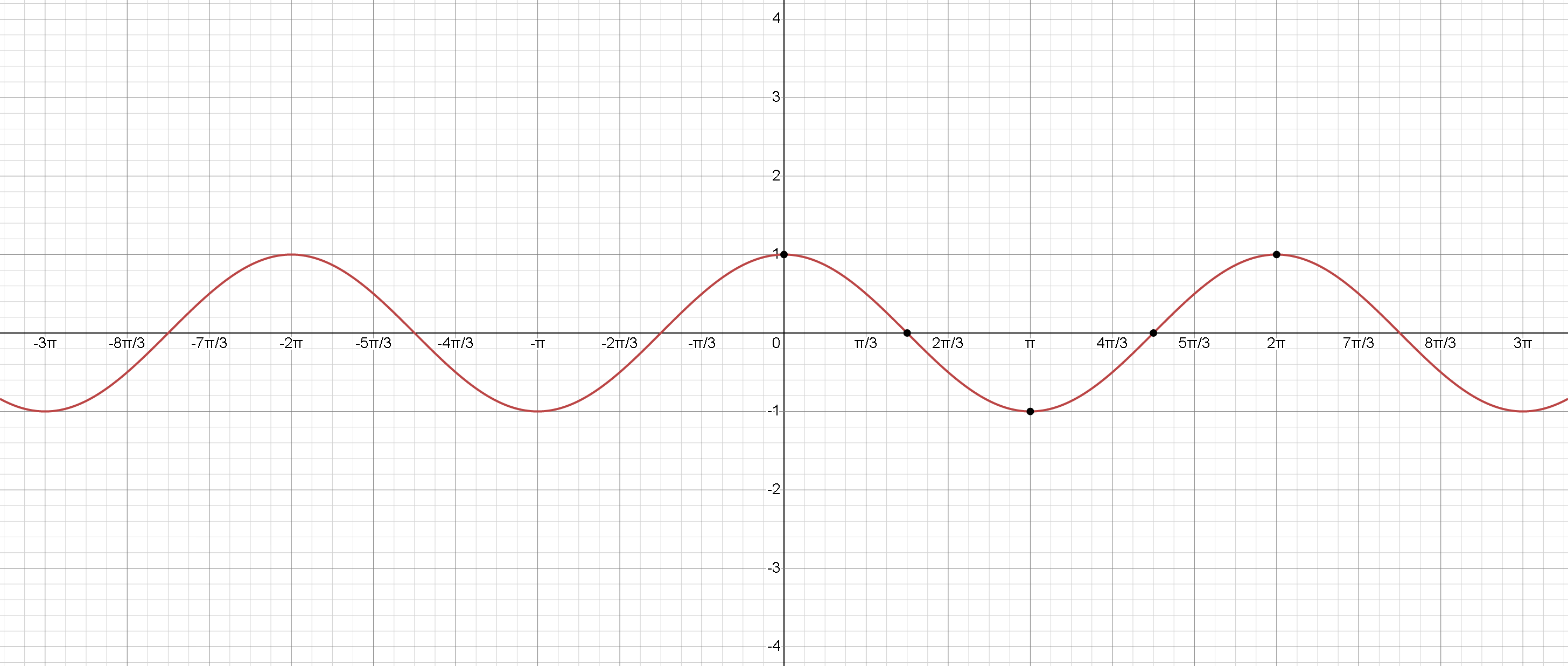
Функция косинуса, подобно функции синуса, имеет период \(2 \pi \) и осциллирует между \(-1\) и \(1\). Однако график функции косинуса сдвинут по фазе на \( \frac{\pi}{2} \) единицы влево по сравнению с функцией синуса. Вот некоторые ключевые точки для функции косинуса:
\( x =0 \), \( \cos(x)=1 \) (максимальное значение)
\( x = \frac{ \pi }{2} \), \( \cos(x)=0 \) (пересечение нуля)
\( x = \pi \), \( \cos(x)= -1 \) (минимальное значение)
\( x= \frac{3 \pi }{2} \), \( \cos(x)=0 \) (пересечение нуля)
\(x = 2 \pi \), \( \cos(x)= 1\) (пересечение нуля и один полный цикл)

Функция косинуса также имеет волновую форму, и ее график симметричен относительно оси \(y\) (четная функция). График также расширяется бесконечно в обе стороны оси \(x\), повторяя свой узор каждые \( 2 \pi \) единицы.

В заключение, графики функций синуса и косинуса представляют собой периодические волноподобные узоры, осциллирующие между \(-1\) и \(1\). Они имеют период \( 2 \pi \), при этом функция косинуса сдвинута по фазе на \( \frac{\pi }{2} \) единицы влево по сравнению с функцией синуса. Эти графики помогают в визуализации свойств и поведения функций синуса и косинуса, которые являются фундаментальными в тригонометрии и различных приложениях в математике, науке и инженерии.

Преобразования синусоидальных и косинусоидальных функций☰

Преобразования синусоидальных и косинусоидальных функций заключаются в изменении базовых синусоидальных и косинусоидальных функций для создания новых функций с различными свойствами, такими как амплитуда, период, сдвиг фазы и вертикальный сдвиг. Эти преобразования позволяют моделировать широкий спектр периодических явлений в различных областях, таких как физика, инженерия и музыка. Базовые синусоидальная и косинусоидальная функции задаются следующим образом:
\( f(x) = \sin(x) \)
\( g(x) = \cos(x) \)

Вот краткий обзор четырех распространенных преобразований:

Амплитуда: Амплитуда - это максимальное значение функции или максимальное расстояние от центральной оси функции. Изменение амплитуды включает умножение синусоидальной или косинусоидальной функции на постоянную \(A\):
\( f(x)= A\sin(x) \)
\( g(x) = A\cos(x) \)

Если \( A > 1 \), амплитуда увеличивается, и если \( 0 < A < 1 \), амплитуда уменьшается. Если \(A\) отрицательно, функция отражается относительно горизонтальной оси.

Период: Период - это интервал, в течение которого функция повторяется. Для изменения периода синусоидальной или косинусоидальной функции мы умножаем независимую переменную \((x)\) на постоянную \(B\):
\( f(x) = \sin(Bx) \)
\( g(x) = \cos(Bx) \)

Новый период функции находится путем деления исходного периода (\( 2 \pi \) как для синусоидальной, так и для косинусоидальной функции) на абсолютное значение \(B\):
\( \text{Новый период } = \frac{2 \pi }{ |B| } \). Если \( B > 1 \), функция сжимается горизонтально, и если \( 0 < B < 1 \), функция растягивается горизонтально.

Сдвиг фазы: Сдвиг фазы - это горизонтальный сдвиг функции. Он достигается путем добавления или вычитания постоянной \(C\) из независимой переменной \((x)\):
\( f(x) = \sin( B \cdot (x-C) ) \)
\( g(x) = \cos ( B \cdot (x-C) ) \)

Положительный сдвиг фазы \( (C > 0 ) \) перемещает функцию вправо, а отрицательный сдвиг фазы \( (C < 0) \) перемещает функцию влево.

Вертикальный сдвиг: Вертикальный сдвиг перемещает функцию вверх или вниз путем добавления или вычитания постоянной \(D\) из всей функции:
\( f(x) = A\sin(B(x - C)) + D \)
\( g(x) = A\cos(B(x - C)) + D \)

Положительный вертикальный сдвиг \((D > 0) \) перемещает функцию вверх, а отрицательный вертикальный сдвиг \( (D < 0) \) перемещает функцию вниз.

В заключение, преобразования синусоидальных и косинусоидальных функций заключаются в изменении их амплитуды, периода, сдвига фазы и вертикального сдвига для моделирования различных периодических явлений. Общие преобразованные синусоидальные и косинусоидальные функции можно записать следующим образом:
\( f(x) = A\sin(B(x-C))+D \)
\( g(x) = A\cos(B(x-C))+D \)

Чтобы продолжить изучение преобразований синусоидальных и косинусоидальных функций, давайте рассмотрим некоторые примеры и применения этих преобразований.

Пример 1: Обработка сигналов
В обработке сигналов амплитудная модуляция \((AM)\) - это техника, используемая для передачи информации путем изменения амплитуды непрерывного сигнала волн. Модуляция может быть представлена произведением несущей волны и информационного сигнала:
\( y(t)= (A + M\sin(Bmt)) \cdot \cos(Bc\cdot t) \)

Здесь \(A\) представляет амплитуду несущей волны, \(Bc\) - угловую частоту несущей волны, \(M\) - амплитуду информационного сигнала, \(Bm\) - угловую частоту информационного сигнала, и \(t\) - переменную времени. Преобразование позволяет сочетать высокочастотную несущую волну с низкочастотным информационным сигналом.

Пример 2: Физика - Простое гармоническое движение
В физике простое гармоническое движение \((SHM)\) описывает движение осциллирующего объекта, такого как масса, прикрепленная к пружине или маятник. Смещение объекта от его равновесного положения в зависимости от времени можно описать с помощью синусоидальной или косинусоидальной функции:
\( x(t) = A\cos(\omega t + \varphi) \)

Здесь \(A\) - амплитуда движения, \( \omega \) - угловая частота, \(t\) - время, и \( \varphi \) - угловая фаза. Угловая фаза определяет начальное положение объекта при \(t = 0\). Простое гармоническое движение можно анализировать и прогнозировать с использованием преобразованных синусоидальных и косинусоидальных функций.

Пример 3: Звук и музыка
В акустике звуковые волны можно моделировать с помощью синусоидальных и косинусоидальных функций. Форма волны чистого тона может быть представлена следующим образом:
\( y(t) = A\sin(2 \pi f \cdot t + \varphi ) \)

Здесь \(A\) - амплитуда звуковой волны, определяющая громкость; \(f\) - частота звуковой волны, определяющая высоту тона; \(t\) - временная переменная, а \( \varphi \) - угловая фаза, определяющая начальное положение волны. Преобразуя синусоидальные и косинусоидальные функции, мы можем анализировать и синтезировать сложные звуки и музыку.

Эти примеры иллюстрируют универсальность преобразованных синусоидальных и косинусоидальных функций в различных областях. Изменяя амплитуду, период, сдвиг фазы и вертикальный сдвиг, мы можем моделировать широкий спектр периодических явлений и решать задачи в различных дисциплинах.

Графики функций тангенса и котангенса☰

Тангенс и котангенс - это тригонометрические функции, которые связаны с синусом и косинусом. Они периодические и обладают уникальными свойствами, что делает их интересными для изучения. Вот более подробный взгляд на графики этих двух функций:

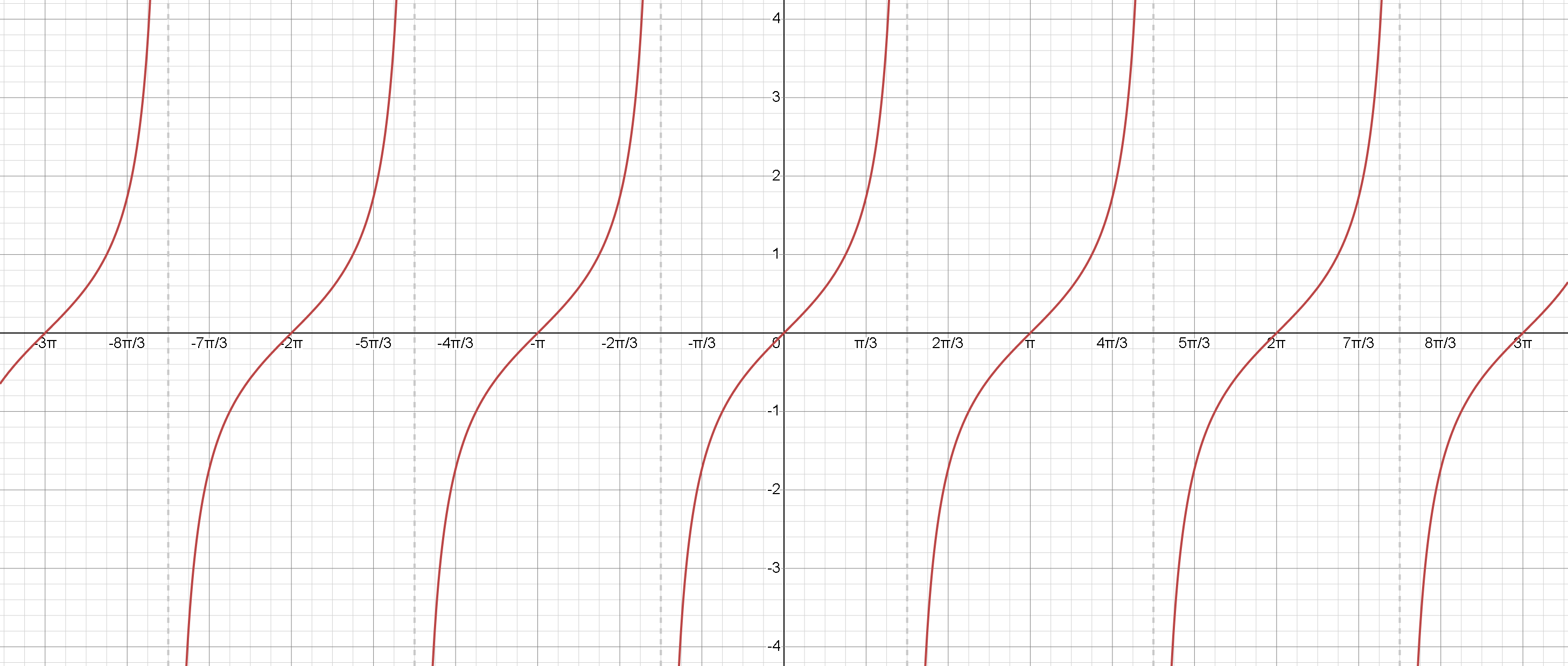
1. Функция тангенса \( tan(x) \):
Функция тангенса определяется как отношение синуса к косинусу, т.е.
\( tan(x) = \frac{sin(x)}{cos(x)} \)

Основные особенности графика тангенса:

• Период: Функция тангенса имеет период \( \pi \), что означает, что она повторяется каждые \( \pi \) единиц вдоль оси \(x\).
• Асимптоты: Поскольку функция тангенса является отношением синуса и косинуса, она неопределена, когда косинус равен нулю. Это происходит при нечетных кратных \( \frac{ \pi }{2} \). ( \( \pm \frac{ \pi }{2} \), \( \pm \frac{ 3 \pi }{2} \), и так далее.).
  Эти точки - места, где находятся вертикальные асимптоты.
• Область значений: Область значений функции тангенса - (\( - \infty ; \infty ) \), поскольку функция принимает все действительные значения.
• Симметрия: Функция тангенса является нечетной функцией, что означает, что она симметрична относительно начала координат.
  Иными словами, \( tg(-x) = -tg(x) \)
• Возрастание: Функция тангенса всегда возрастает на каждом из своих периодов.

2. Функция котангенса cot(x):
Функция котангенса определяется как отношение косинуса к синусу, т.е.
\( cot(x) = \frac{cos(x)}{sin(x)} \)

Основные особенности графика котангенса:

• Период: Функция котангенса имеет период \( \pi \), что означает, что она повторяется каждые \( \pi \) единиц вдоль оси \(x\), как и функция тангенса.
• Асимптоты: Поскольку функция котангенса является отношением косинуса и синуса, она неопределена, когда синус равен нулю. Это происходит при целых кратных \( \pi\). (0, \( \pm \pi\), \( \pm 2 \pi \), и так далее). Эти точки - места, где находятся вертикальные асимптоты.
• Область значений: Область значений функции котангенса - \( (- \infty, \infty ) \), поскольку функция принимает все действительные значения.
• Симметрия: Функция котангенса является нечетной функцией, что означает, что она симметрична относительно начала координат.
  Иными словами, \(cot(-x)=-cot(x)\).
• Убывание: Функция котангенса всегда убывает на каждом из своих периодов.

В заключение, как функция тангенса, так и функция котангенса периодические, с периодом \( \pi \), и обладают нечетной симметрией. У них разные вертикальные асимптоты и поведение, с функцией тангенса возрастающей, а функцией котангенса - убывающей.

Обратные тригонометрические функции ☰

Обратные тригонометрические функции, также известные как арк-функции или анти-тригонометрические функции, являются обратными функциями основных тригонометрических функций: синуса, косинуса и тангенса. Эти функции позволяют найти угол, когда известно тригонометрическое значение. Существует шесть основных обратных тригонометрических функций:

1. Обратный синус. \( sin^{-1} (x) \) или \( arcsin(x) \):
Обратная функция синуса.
Область определения: \( [-1 , 1 ] \)
Область значений: \( [- \frac{ \pi }{2}, \frac{ \pi }{2} ] \)

2. Обратный косинус. \( cos^{-1} (x) \) или \( arccos(x) \):
Обратная функция косинуса.
Область определения: \( [-1 , 1 ] \)
Область значений: \( [ 0 , \pi ] \)

3. Обратный тангенс. \( tan^{-1} (x) \) или \( arctan(x) \):
Обратная функция тангенса.
Область определения: ( \(- \infty , \infty \) )
Область значений: ( \( - \frac{ \pi }{2}, \frac{ \pi }{2} \) )

4. Обратный косеканс. \( csc^{-1} (x) \) или \( arccsc(x) \):
Обратная функция косеканса (которая является обратной функцией синуса).
Область определения: \( (-\infty, -1] \cup [1, \infty) \)
Область значений: \( \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right]\)

5. Обратный секанс. \( sec^{-1} (x) \) или \( arcsec(x) \):
Обратная функция секанса (которая является обратной функцией косинуса).
Область определения: \( \left(-\infty, -1\right] \cup \left[1, \infty\right) \)
Область значений: \( \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] \)

6. Обратный котангенс. \( cot^{-1} (x) \) или \( arccot(x) \):
Обратная функция котангенса.
Область определения: ( \(- \infty , \infty \) )
Область значений: ( \( 0 , \pi \) )


Свойства обратных тригонометрических функций:

⠐ Ограниченные области определения и области значений: Для того чтобы тригонометрические функции были обратимыми, их области определения ограничиваются, что приводит к ограниченным областям значений обратных тригонометрических функций.

⠐ Нотация: Обратные тригонометрические функции часто обозначаются с префиксом "\( ^{-1} \)" или " \(arc\)". Например, \( sin^{-1} (x) \) или \(arcsin(x) \) представляют собой обратную функцию синуса.
Обратите внимание, что \( sin^{-1} (x) \) НЕ то же самое, что \( \frac{1}{sin(x)} \) , что является обратной функцией (косекансом).

⠐ Композиция:
Композиция тригонометрической функции и ее обратной функции приводит к тождественной функции, при условии, что входное значение находится в правильном диапазоне:

\( sin( arcsin(x) ) = x \), Если \(x\) находится в области определения \( arcsin( [-1,1] ) \)

\( arcsin ( sin(x) ) = x \), Если \(x\) находится в области значений \( arcsin( [ -\frac{ \pi }{2} , \frac{ \pi }{2} ] ) \)

Аналогичные отношения справедливы для других обратных тригонометрических функций.

⠐ Дифференцируемость:
Обратные тригонометрические функции дифференцируемы в пределах своих областей определения, за исключением точек, где у исходных тригонометрических функций вертикальные касательные.
Например, обратные функции синуса и косинуса не дифференцируемы при \(x=-1\) и \(x=1\), а обратная функция тангенса не дифференцируема при \(x=- \infty \) и \(x= \infty \).

⠐ Симметрия:
Некоторые обратные тригонометрические функции обладают симметрией.
Например:
\( arctan(-x) = -arctan(x) \) : Обратная функция тангенса является нечетной функцией.

\( arccot(-x) = \pi - arcctg(x) \) : Обратная функция котангенса обладает определенным типом симметрии.

Обратные тригонометрические функции крайне важны для решения задач, связанных с треугольниками и тригонометрией, особенно когда необходимо найти угол при известных длинах сторон или других тригонометрических значениях. Они используются в различных областях математики, физики и инженерии, таких как в исчислении, геометрии и изучении периодических явлений.

⠐ Производные:
Производные обратных тригонометрических функций имеют важное значение в исчислении, особенно при решении задач интегрирования, связанных с тригонометрическими функциями. Вот производные трех основных обратных тригонометрических функций:

\( \frac{d (\arcsin(x))}{dx} = \frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arccos(x))}{dx} = -\frac{1}{\sqrt{1 - x^2}} \)

\( \frac{d (\arctan(x))}{dx} = \frac{1}{1 + x^2} \)