Уравнение полинома степени (Уравнения полиномов более высокой степени)
Полиномиальное уравнение степени \(n\) представляет собой уравнение вида \( a_n x^n+a_{n-1} x^{n-1}+⋯+a_1 x+a_0=0 \), где \(a_n, a_{n-1}, …, a_1 ,a_0 \) - константы, а \(n\) - неотрицательное целое число. Здесь \(x\) - переменная.
Степень полиномиального уравнения - это наивысшая степень переменной \(x\) в уравнении.
Например, уравнение \(2x^3-5x^2+3x-7=0\) - это полиномиальное уравнение степени 3, потому что наивысшая степень \(x\) равна 3. Термин с постоянным членом \(a_0\) также включается в сумму, хотя не включает \(x\), чтобы было ясно, что это полиномиальное уравнение.
Решения полиномиального уравнения степени \(n\) называются корнями или нулями полинома. Основная теорема алгебры утверждает, что полином степени \(n\) имеет ровно \(n\) комплексных корней, учитывая кратности. Это означает, что есть ровно \(n\) решений уравнения \( a_n x^n +a_{n-1} x^{n-1} +⋯+a_1 x+ a_0 = 0 \), если мы разрешаем комплексные значения \(x\).
Существует несколько техник для нахождения корней полиномиальных уравнений степени \(n\). Например, если \(n=1\), то уравнение \(ax+b=0\) имеет один корень, который равен \(x=- \frac{b}{a} \). Для квадратных уравнений вида \( ax^2 +bx+c=0 \), мы можем использовать квадратную формулу для нахождения корней. Для кубических уравнений вида \(ax^3+bx^2+cx+d=0 \), также
существует формула, называемая
формулой Кардано
, которая дает корни в терминах коэффициентов \(a\), \(b\), \(c\), \(d\). Однако эта формула может быть довольно сложной для использования на практике. Для полиномиальных уравнений степени более 3 нет общей формулы, которая дает корни в терминах коэффициентов, хотя есть некоторые особые случаи, где корни можно найти с использованием других методов.
В общем случае нахождение корней полиномиального уравнения степени \(n\) включает факторизацию полинома на линейные и квадратные множители, а затем решение каждого из множителей отдельно.
Например, рассмотрим полиномиальное уравнение \(x^3-3x^2+2x=0\). Мы можем разложить его как \(x(x-1)(x-2)=0\), что дает три решения: \(x=0\), \(x=1\) и \(x=2\). Это корни полиномиального уравнения.
Уравнения полиномов более высокой степени
- это уравнения степени 4 и выше, такие как квадратные уравнения \( (ax^4+bx^3+cx^2+dx+e=0) \) и кубические уравнения \( (ax^5+bx^4+cx^3+dx^2+ex+f=0) \). Эти уравнения могут быть более сложными для решения, чем уравнения с более низкой степенью полинома, и могут требовать более сложных методов, таких как использование комплексных чисел и теории групп.
Одним из важных результатов в теории полиномиальных уравнений является основная теорема алгебры, которая утверждает, что у каждого не постоянного полиномиального уравнения с комплексными коэффициентами есть как минимум один комплексный корень. Это означает, что даже если полиномиальное уравнение не может быть решено с использованием действительных чисел, его всегда
можно решить с помощью комплексных чисел.
Существует несколько техник для решения уравнений полиномов более высокой степени. Один из подходов - попытаться разложить уравнение на более простые полиномы.
Например, квадратное уравнение \( x^4-5x^2+4=0 \) может быть разложено как \((x^2-4)(x^2-1)=0 \), что дает корни \( x = \pm 1 \) и \( x = \pm 2 \). Однако не все уравнения полиномов более высокой степени могут быть разложены таким образом.
Другой подход - использовать численные методы для приближенного нахождения корней уравнения. Например, метод Ньютона-Рафсона можно использовать для итеративного нахождения все более точных приближений к корням. Однако эти методы не гарантируют точного решения и могут потребовать большого числа итераций для сходимости.
Для уравнений пятой степени и более высокой степени полиномов нет общей формулы для нахождения корней в терминах коэффициентов, как для квадратных, кубических и квадратичных уравнений. Это было доказано математиком Эваристом Галуа в 19 веке с использованием теории групп. Вместо этого конкретные уравнения могут быть решены с использованием специализированных методов
или приближены с использованием численных методов.
Рациональные уравнения
Рациональные уравнения - это уравнения, которые включают рациональные выражения, которые представляют собой отношения двух полиномов. Полином - это выражение, которое состоит из одного или нескольких членов, содержащих переменные с целыми степенями и коэффициенты, которые могут быть вещественными или комплексными числами.
Рациональные уравнения обычно записываются в форме: \( \frac{P(x)}{Q(x)} =\frac{R(x)}{S(x)} \), где \(P(x)\), \(Q(x)\), \(R(x)\) и \(S(x)\) - полиномы, и \(Q(x) \neq 0 \) и \(S(x) \neq 0\).
Основная цель при решении рациональных уравнений - найти значения переменной \(x\), которые делают уравнение истинным. Для решения рационального уравнения первым шагом является очистка знаменателей, умножая обе стороны уравнения на общий знаменатель двух рациональных выражений. Его можно найти, умножив знаменатели \(Q(x)\) и \(S(x)\) и упростив полученное выражение.
После очистки знаменателей уравнение превращается в уравнение полинома, которое можно решить с использованием стандартных алгебраических методов. После нахождения решений для \(x\) важно проверить их в исходном уравнении, чтобы убедиться, что они являются допустимыми решениями. Если решение делает один или оба знаменателя равными нулю, оно не является допустимым
решением и должно быть исключено.
Пример: Решите уравнение \(\frac{1}{x+1} + \frac{1}{x-1} = \frac{10}{x^2-1} \).
Шаг 1: Найдите общий знаменатель. В этом случае общим знаменателем является \((x+1)(x-1)\), поэтому мы можем переписать уравнение как:
\( \frac{1}{x+1} \cdot \frac{x-1}{x-1} + \frac{1}{x-1} \cdot \frac{x+1}{x+1} = \frac{10}{(x+1) \cdot (x-1)} \) ;
Упрощая, мы получаем:
\(\frac{x-1}{(x+1)(x-1)} + \frac{x+1}{(x+1)(x-1)} = \frac{10}{(x+1)(x-1)} \) ;
Объединяя дроби, мы получаем:
\(\frac{2x}{(x+1)(x-1)} = \frac{10}{(x+1)(x-1)} \)
Шаг 2: Избавьтесь от знаменателей, умножив обе стороны уравнения на общий знаменатель: \(2x=10\).
Шаг 3: Найдите \(x\). \(x = 5\).
Шаг 4: Проверьте на фиктивные решения. Поскольку \(x=5\) делает знаменатель \((x^2-1)\) ненулевым, нет фиктивных решений для проверки.
Следовательно, решением уравнения \(\frac{1}{x+1} + \frac{1}{x-1} = \frac{10}{x^2-1} \) является \(x=5\).
Уравнение модуля переменной
Уравнение модуля переменной - это тип уравнения, который включает в себя модуль переменной. Модуль числа - это расстояние от нуля на числовой прямой, поэтому модуль переменной можно представить как расстояние от нуля, которое может принимать переменная.
Общая форма уравнения модуля выглядит так: \(|f(x)|=g(x) \), где \(f(x) \) - это некоторое выражение, содержащее переменную \(x\), а \(g(x)\) - другое выражение, которое может содержать или не содержать \(x\). Цель при решении уравнения модуля состоит в том, чтобы найти все значения переменной \(x\), которые делают уравнение истинным. Основной подход к решению
уравнений модуля заключается в разделении уравнения на два случая, один - когда \(f(x)\) положителен, и другой - когда \(f(x)\) отрицателен. Это потому, что модуль положительного числа равен самому числу, а модуль отрицательного числа - его противоположности. Таким образом, если мы знаем, положительное ли \(f(x)\) или отрицательное, мы можем определить значение
\(|f(x)|\) и решить уравнение.
Например, рассмотрим уравнение: \(|x-3|=5\).
Мы начинаем с разделения его на два случая:
Случай 1: \(x-3\) положителен.
\(x-3=5\).
\(x=8\).
Случай 2: \(x-3\) отрицателен.
\(-(x-3)=5\).
\(-x+3=5\).
\(x=-2\).
Следовательно, решения уравнения: \(x=8\) и \(x=-2\).
Также возможно, что у уравнения модуля нет решений. Например, рассмотрим уравнение: \(|x-3|=-2\).
Поскольку модуль любого числа всегда неотрицательный, нет значения \(x\), которое делает левую часть уравнения равной отрицательному числу. Следовательно, это уравнение не имеет решений.
В заключение, решение уравнений модуля заключается в разделении уравнения на два случая в зависимости от того, положителен ли аргумент внутри модуля или отрицателен, решении каждого случая отдельно, а затем объединении решений. Важно проверить, что любые найденные решения действительно удовлетворяют исходному уравнению, так как некоторые уравнения могут не иметь
решений или иметь вымышленные решения, которые на самом деле не работают.
Иррациональные уравнения
Иррациональные уравнения - это уравнения, которые включают одну или несколько иррациональных функций или иррациональных выражений. Иррациональная функция - это функция, которая не может быть выражена в виде отношения двух многочленов. Обычные примеры иррациональных функций включают функцию квадратного корня \( f(x) = \sqrt{x} \), функцию кубического корня \( f(x) =
\sqrt[3]{x} \) и логарифмическую функцию \(f(x)=ln(x) \).
Общая форма иррационального уравнения: \(f(x)=g(x) \), где \(f(x)\) и \(g(x)\) являются иррациональными функциями или выражениями. Решение таких уравнений обычно заключается в выделении иррационального выражения на одной стороне уравнения, а затем возведении обеих сторон в квадрат, что может устранить радикал. Однако этот метод может привести к появлению лишних
решений, которые не удовлетворяют исходному уравнению.
Для иллюстрации рассмотрим следующий пример: \( \sqrt{x+1}-\sqrt{x-1}=1 \).
Чтобы решить это уравнение, мы можем возвести обе стороны в квадрат:
\( (\sqrt{x+1}-\sqrt{x-1})^2 = 1^2\)
\((x+1) - 2\sqrt{x+1} \cdot \sqrt{x-1} + (x-1) = 1 \)
\( 2\sqrt{x+1} \cdot \sqrt{x-1} = 2x-1 \)
\( (\sqrt{x+1} \cdot \sqrt{x-1})^2 = \left(\frac{2x-1}{2}\right)^2 \)
\( (x+1)(x-1) = \left(\frac{2x-1}{2}\right)^2 \)
\( x^2 - 1 = \frac{(2x-1)^2}{4} \)
\( 4x^2 - 4 = 4x^2 - 4x + 1 \)
\( -4x = -5 \)
\( x = \frac{5}{4} \)
Однако мы должны проверить наше решение, чтобы убедиться, что оно не является лишним.
Уравнения в двух переменных. Система уравнений.
Уравнения в двух переменных - это математические выражения, которые связывают две переменные, обычно обозначаемые как \(x\) и \(y\), знаком равенства. Эти типы уравнений представлены в форме: \(ax+by=c\), где \(a\), \(b\), \(c\) - константы, \(x\) и \(y\) - переменные. Значения \(x\) и \(y\), которые удовлетворяют уравнению, называются решениями или корнями
уравнения.
График уравнения в двух переменных представляет собой прямую на декартовой координатной плоскости, где \(x\) - горизонтальная ось, а \(y\) - вертикальная ось. Стандартная форма уравнения прямой - это: \(y=mx+b\), где \(m\) - это угловой коэффициент прямой, а \(b\) - это \(y\)-перехват, точка, где прямая пересекает \(y\)-ось.
Чтобы преобразовать уравнение из стандартной формы в форму с угловым коэффициентом, мы можем решить уравнение относительно \(y\):
\( ax+by=c \)
\( by=-ax+c \)
\( y= - \frac{a}{b} \cdot x + \frac{c}{b} \)
Таким образом, угловой коэффициент прямой равен \( m=-\frac{a}{b} \), а \(y\)-перехват равен \( b= \frac{c}{b} \).
Обратно, чтобы преобразовать уравнение из формы с угловым коэффициентом в стандартную форму, мы можем переставить члены:
\(y=mx+b\)
\( -mx+y=b \)
\( ax+by=c \)
где \(a=-m\), \(b=1\) и \(c=b\).
Для решения системы уравнений с двумя переменными мы должны найти значения \(x\) и \(y\), которые удовлетворяют обоим уравнениям одновременно. Один из способов сделать это - построить графики двух уравнений и найти точку, в которой прямые пересекаются. Эта точка представляет собой решение системы.
Другой метод решения системы уравнений с двумя переменными - это метод подстановки. В этом методе мы решаем одно из уравнений относительно одной из переменных и подставляем выражение в другое уравнение. Это приведет к уравнению с одной переменной, которое мы можем решить, чтобы найти значение переменной. Затем мы можем подставить это значение обратно в одно из
исходных уравнений, чтобы найти значение другой переменной.
Например, рассмотрим систему уравнений:
\( \begin{cases} 2x+y=4 \\ x-y=1 \end{cases} \)
Решив второе уравнение относительно \(x\), мы получаем: \(x=y+1\) .
Подставив это выражение в первое уравнение, мы получаем: \( 2(y+1)+y=4 \).
Упростив и решив уравнение относительно \(y\), получаем: \(3y=2\) , \(y= \frac{2}{3} \).
Подставив это значение обратно в уравнение \(x=y+1\), получаем: \(x= \frac{2}{3}+1 \), \(x= \frac{5}{3} \).
Таким образом, решением системы является \( ( \frac{5}{3} , \frac{2}{3} ) \).
В заключение, уравнения в двух переменных - это математические выражения, которые связывают две переменные знаком равенства, а их графики - это прямые линии на декартовой координатной плоскости. Для решения системы уравнений с двумя переменными мы можем использовать методы графика или подстановки, чтобы найти значения \(x\) и \(y\), которые удовлетворяют обоим
уравнениям одновременно.
Система уравнений.
Система уравнений - это набор из двух или более уравнений с одинаковыми переменными. Переменные в системе уравнений представляют собой одни и те же значения в каждом уравнении. Мы можем решить систему уравнений, найдя значения переменных, которые удовлетворяют всем уравнениям в системе.
Существуют различные методы решения системы уравнений, такие как графический, подстановочный и исключительный. Выбираемый метод зависит от сложности системы и личных предпочтений.
Один из способов решения системы уравнений - графический. Графический метод позволяет нам визуализировать решения системы как точки пересечения графиков уравнений. Для построения графиков уравнений мы отмечаем точки на декартовой плоскости, удовлетворяющие каждому уравнению, затем соединяем точки линиями. Точки пересечения линий представляют собой решения системы.
Например, рассмотрим систему уравнений:
\( \begin{cases} y = 2x + 1 \\ y = -\frac{1}{3}x + 4 \end{cases} \)
Для построения графиков этих уравнений мы можем выбрать несколько значений \(x\) и подставить их в каждое уравнение, чтобы найти соответствующие значения \(y\). Затем мы отмечаем полученные точки и соединяем их линиями.
Для первого уравнения:
| \(x\) | \(y=2x+1\) |
|---|---|
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
Для второго уравнения:
| \(x\) | \(y=-\frac{1}{3} x +4 \) |
|---|---|
| -3 | 5 |
| 0 | 4 |
| 3 | 3 |
Теперь мы можем построить эти точки и соединить их, чтобы образовать линии:

Точка пересечения линий - это решение системы, которое приблизительно равно \((1.3, 3.6)\).
Другой метод решения системы уравнений - подстановка. В этом методе мы решаем одно из уравнений для одной из переменных, затем подставляем выражение в другое уравнение. Это приводит к уравнению с одной переменной, которое мы можем решить, чтобы найти значение переменной. Затем мы можем подставить это значение обратно в одно из исходных уравнений, чтобы найти
значение другой переменной.
Система уравнений, в которой одно уравнение первой степени, а другое - второй степени
Система уравнений - это набор уравнений, рассматриваемых вместе как группа. Система уравнений, в которой одно уравнение первой степени (линейное), а другое уравнение второй степени (квадратное), является типом нелинейной системы уравнений.
Общий вид уравнения первой степени: \(ax+b=0\), где \(a\) и \(b\) - константы, а \(x\) - переменная.
Общий вид уравнения второй степени: \( ax^2+bx+c=0 \), где \(a\), \(b\) и \(c\) - константы, а \(x\) - переменная.
Для решения системы уравнений, в которой одно уравнение первой степени, а другое уравнение второй степени, существует несколько методов, включая:
- Метод подстановки: В этом методе мы решаем одно из уравнений для одной из переменных относительно другой переменной, а затем подставляем это выражение в другое уравнение. Это приводит к квадратному уравнению с одной переменной, которое мы можем решить, используя квадратную формулу или факторизацию. Как только мы найдем значение(я) переменной, мы можем подставить его(их) обратно в одно из исходных уравнений, чтобы найти значение(я) другой переменной.
- Метод исключения: В этом методе мы исключаем одну из переменных, умножая одно или оба уравнения на постоянную величину так, чтобы коэффициенты одной из переменных были равны и противоположны в двух уравнениях. Это приводит к уравнению с одной переменной, которое мы можем решить, а затем подставить обратно в одно из исходных уравнений, чтобы найти значение(я) другой переменной.
Например, рассмотрим следующую систему уравнений:
\( \begin{cases} x + 2y = 3 \\ x^2 - 4y^2 = 0 \end{cases} \)
Из второго уравнения мы можем выделить общий множитель \( x^2 - 4y^2 \) как \( (x+2y)(x-2y)=0 \).
Это дает нам две возможности: \( x+2y=0 \) или \( x-2y=0 \)
Если мы решим первое уравнение относительно \(x\) как \(x=-2y\), мы можем подставить это во второе уравнение, чтобы получить:
\( (-2y)^2-4y^2=0 \)
\( 4y^2-4y^2=0 \)
Это упрощается до \(0=0\), что верно для любого значения \(y\). Следовательно, у нас бесконечно много решений, которые можно выразить как \( (x,y)=(-2t,t) \), где \(t\) - любое действительное число.
Если мы решим второе уравнение относительно \(x\) как \(x=2y\), мы можем подставить это в первое уравнение, чтобы получить:
\( 2y+2y=3 \)
\( 4y=3 \)
\( y = \frac{3}{4} \)
Подставляя это в \(x=2y\), мы получаем \( x= \frac{3}{2} \). Следовательно, у нас есть одно решение, которое составляет \( (x,y)=( \frac{3}{2} , \frac{3}{4} ) \).
Графический метод:
В этом методе мы строим обе уравнения на одной координатной плоскости и ищем точку(и) пересечения, которые представляют собой решения системы уравнений. Однако этот метод не всегда может быть выполним для сложных систем уравнений.
В заключение, систему уравнений, в которой одно уравнение первой степени, а другое уравнение второй степени, можно решить с использованием различных методов, включая подстановку, исключение и графические методы. Выбор метода зависит от конкретной системы уравнений и индивидуальных предпочтений решателя.
Система двух уравнений второй степени в двух переменных
Система двух уравнений второй степени в двух переменных представляет собой набор из двух уравнений в двух переменных, где каждое уравнение является уравнением второй степени. Общая форма такой системы выглядит следующим образом:
\( ax^2+by^2+cx+dy+e=0 \)
\( fx^2+gy^2+hx+iy+j=0 \)
где \(a\), \(b\), \(c\), \(d\), \(e\), \(f\), \(g\), \(h\), \(i\), \(j\) - константы, а \(x\), \(y\) - переменные.
Этот тип системы является нелинейным, что означает, что решения системы не обязательно образуют прямую линию. Вместо этого решения могут быть кривыми или наборами дискретных точек в плоскости \(xy\).
Для решения этой системы одним из возможных методов является использование подстановки для исключения одной переменной и сведения системы к одному уравнению в одной переменной. Это включает решение одного из уравнений для x или y, а затем подстановку этого выражения в другое уравнение. Полученное уравнение будет одним уравнением второй степени в одной переменной,
которое можно решить с использованием методов, таких как факторизация или квадратичная формула.
Другим возможным методом является использование метода исключения, который включает в себя сложение или вычитание двух уравнений для исключения одной из переменных. Это можно сделать, умножив одно или оба уравнения на константы, при необходимости, чтобы создать коэффициенты, которые будут уничтожены при сложении или вычитании уравнений.
Решениями системы будут значения \(x\) и \(y\), которые удовлетворяют обоим уравнениям одновременно. В зависимости от конкретных уравнений в системе может быть одно или несколько решений, или совсем нет решений. Построение графиков уравнений в плоскости \(xy\) может обеспечить визуальное представление возможных решений и помочь понять поведение системы.
Примером системы двух уравнений второй степени в двух переменных является:
\( \begin{cases} x^2+y^2=25 \\ x^2-y^2=9 \end{cases} \)
Эта система представляет собой пересечение окружности с центром в начале координат радиусом 5 и гиперболы с вертикальной осью и центром в начале координат.
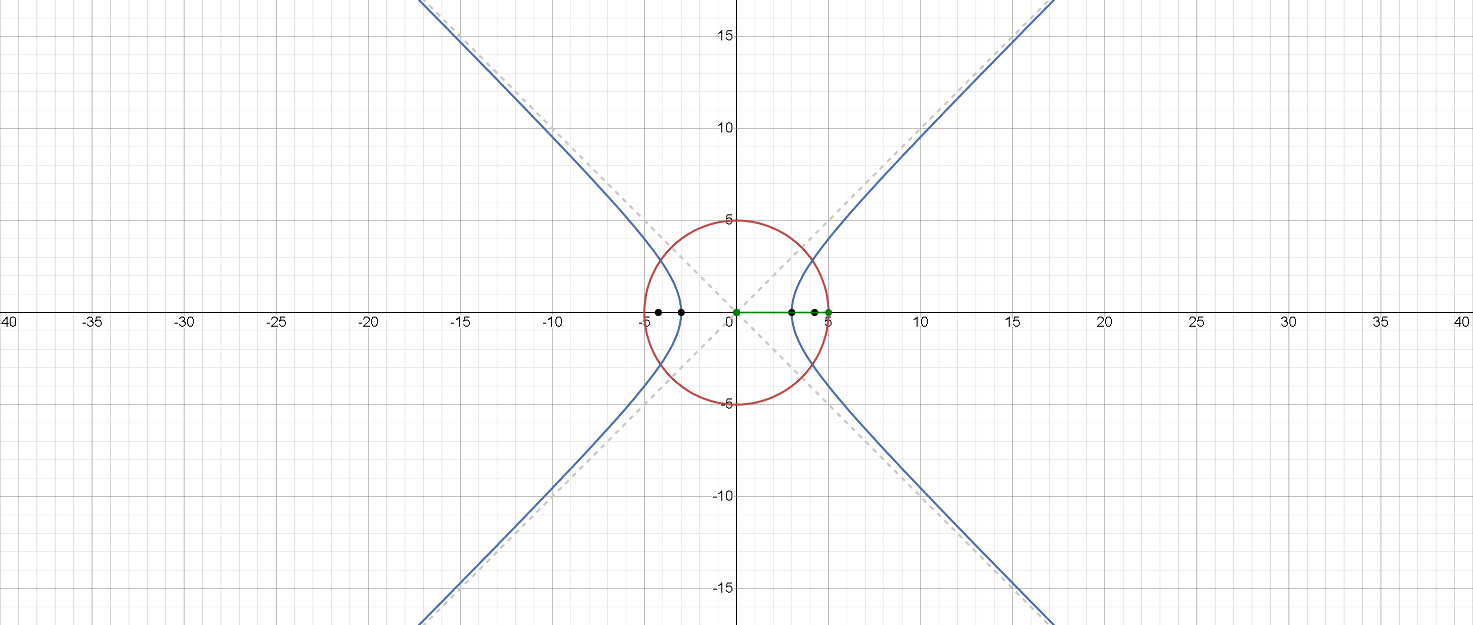
Из этого графика мы можем сказать, что система имеет четыре решения.
Сложим два уравнения, получим:
\( \begin{cases} x^2+y^2=25 \\ +\\ x^2-y^2=9 \end{cases} \)
\(2x^2 = 34\)
\( x^2 = 17 \).
Возьмем квадратный корень от обеих сторон, получим \( x = \pm \sqrt{17} \). Подставив эти значения обратно в одно из исходных уравнений, мы можем решить для \(y\). Например, используя первое уравнение, мы имеем:
\( (\sqrt{17})^2 + y^2 = 25 \)
\( y^2 = 8 \)
\( y = \pm 2 \sqrt{2} \)
Таким образом, решениями системы являются:
\( (\sqrt{17}, 2 \sqrt{2}) \),
\( (\sqrt{17}, -2 \sqrt{2}) \),
\( (-\sqrt{17}, 2 \sqrt{2}) \)
\( (-\sqrt{17}, -2 \sqrt{2}) \).