Векторы ☰

Векторы - это математические объекты, которые широко используются в различных областях науки, инженерии и математике. Они используются для представления физических величин, таких как сила, скорость, ускорение и перемещение, которые имеют как величину, так и направление.
Вектор обычно представлен стрелкой с длиной и направлением. Длина стрелки представляет собой величину вектора, а направление стрелки - направление вектора. Величина вектора является скалярным значением и обозначается \( \vec{|v|} \).
Векторы могут быть обозначены путем именования их начальной и конечной точек, где начальная точка - хвост вектора, а конечная точка - голова вектора. Например, вектор от точки \(A\) до точки \(B\) может быть обозначен как \( \overrightarrow{AB} \).

Векторы имеют ряд свойств, которые важны в математике и физике. Некоторые из основных свойств векторов включают:

Величина: Векторы имеют величину или длину, которая является неотрицательным скаляром, который представляет собой размер вектора.

Направление: Векторы имеют направление, которое можно указать с помощью углов или других направленных обозначений. Направление вектора определяется углом между вектором и фиксированным направлением.

Сложение: Векторы могут быть сложены вместе с использованием параллелограмма или треугольника закона сложения векторов. Это включает в себя сложение соответствующих компонент каждого вектора для получения результирующего вектора.

Скалярное умножение: Векторы могут быть умножены на скаляры, что изменяет величину и/или направление вектора. Скалярное умножение включает умножение каждой компоненты вектора на скаляр.

Скалярное произведение: Векторы могут быть перемножены с использованием скалярного произведения или скалярного произведения. Скалярное произведение двух векторов является скаляром, который представляет собой произведение их величин и косинуса угла между ними.

Векторное произведение: Векторы также могут быть умножены с использованием векторного произведения или векторного произведения. Векторное произведение двух векторов - это вектор, перпендикулярный обоим исходным векторам и имеющий величину, равную произведению их величин на синус угла между ними.

Нулевой вектор: Существует уникальный вектор, называемый нулевым вектором, обозначаемый \( \vec{0} \), который имеет величину \(0\) и нет направления. Его можно рассматривать как вектор, идущий из одной точки в себя, или, что эквивалентно, как разность любых двух равных векторов.
Например, \( \overrightarrow{OA} - \overrightarrow{OA} = 0 \).

Единичный вектор: Единичный вектор - это вектор с величиной 1. Любой ненулевой вектор может быть разделен на его величину, чтобы получить единичный вектор в том же направлении.

Коллинеарные векторы: Векторы коллинеарны, если они лежат на одной линии или параллельны. Другими словами, они имеют одинаковое или противоположное направление. Коллинеарные векторы могут быть записаны в виде скалярных кратных друг друга. Если два вектора \( \vec{v} \) и \( \vec{w} \) коллинеарны, то существует скаляр \(k\) такой, что \( \vec{v} = k \vec{w} \) или \( \vec{w} = k \vec{v} \). Это означает, что один вектор является скалярным кратным другого, и они указывают в одном или противоположном направлении.

Ортогональные векторы: Два вектора ортогональны, если их скалярное произведение равно нулю. Ортогональные векторы также называются перпендикулярными векторами, и между ними образуется угол 90 градусов.

Базисные векторы: Набор базисных векторов - это набор линейно независимых векторов, которые могут быть использованы для представления любого другого вектора в пространстве. Самые распространенные базисные векторы - это стандартные единичные векторы в трехмерном пространстве, обозначаемые \(\hat{i}\), \(\hat{j}\) и \(\hat{k}\).

Линейная независимость: Набор векторов линейно независим, если ни один из векторов в наборе не может быть выражен как линейная комбинация других. Если набор векторов линейно независим, то он может быть использован в качестве базиса для векторного пространства.

Объем: Объем набора векторов - это набор всех линейных комбинаций этих векторов. Объем набора векторов является подпространством векторного пространства, содержащего эти векторы.

Проекция: Проекция одного вектора на другой является компонентом первого вектора, лежащим в направлении второго вектора. Проекция вектора \( \vec{u} \) на вектор \(\vec{v}\) задается формулой $$ \text{proj}_{\vec{v}} ( \vec{u} ) = \frac{\vec{u} \cdot v}{||\vec{v}||^2} \vec{v} $$

Компонента: Компонента одного вектора вдоль другого - это часть первого вектора, лежащая в направлении второго вектора. Компонента вектора \( \vec{u} \) вдоль вектора \( \vec{v} \) задается формулой $$ \text{comp}_{\vec{v}} (\vec{u}) = \frac{\vec{u} \cdot v}{||\vec{v}||^2} cos \theta $$ где \(\theta \) - угол между \(\vec{u} \) и \(\vec{v} \).

Параллельный транспорт: Параллельный транспорт - это способ перемещения векторов вдоль кривой таким образом, чтобы сохранялось их направление. Параллельный транспорт используется в дифференциальной геометрии и других областях для изучения кривизны кривых и поверхностей.

Ковариация и контравариация: В математике и физике векторы часто классифицируются как ковариантные или контравариантные в зависимости от того, как их компоненты преобразуются при преобразованиях координат. Ковариантные векторы имеют компоненты, которые преобразуются так же, как координаты, в то время как контравариантные векторы имеют компоненты, которые преобразуются противоположным образом. Концепция ковариации и контравариации широко используется в тензорном исчислении и других областях математики и физики.

Это лишь несколько из множества свойств векторов.

Длина вектора (Величина, Модуль вектора) ☰

В математике длина вектора также известна как его величина или модуль вектора. Она представляет собой расстояние между началом и концом вектора в геометрическом пространстве.
Для вектора с компонентами \( (x, y, z) \) в трехмерном пространстве его длина может быть вычислена с использованием следующей формулы:
\( |\vec{v}| = \sqrt{(x^2+ y^2+ z^2 )} \).

В двумерном пространстве формула для длины вектора с компонентами \((x, y)\) выглядит так: \( |\vec{v}| = \sqrt{(x^2+ y^2 )} \).

В общем случае длина вектора может быть вычислена с использованием теоремы Пифагора, которая утверждает, что квадрат длины вектора равен сумме квадратов его компонент.

Направление вектора ☰

Направление вектора можно определить, вычислив его угол относительно опорной оси. Этот угол часто измеряется против часовой стрелки от положительного направления опорной оси.
Если \( \vec{v} \) - вектор в двумерном пространстве с компонентами \( (v_x,v_y ) \), то его направление \( \theta \) определяется по формуле: \( \theta = \arctan \left( \frac{v_y}{v_x} \right) \), где arctan - обратная тангенсная функция.

В трехмерном пространстве вектор \( \vec{v} \) с компонентами \( (v_x,v_y,v_z ) \) может быть представлен в виде направленного отрезка от начала координат \( (0,0,0) \) до точки \( (v_x,v_y,v_z ) \). Его направление может быть описано двумя углами: азимутальным углом \( \varphi \), который измеряется против часовой стрелки от положительной \(x\)-оси в плоскости \(xy\), и полярным углом \( \theta \), который измеряется от положительной \(z\)-оси до отрезка.

Азимутальный угол \( \varphi \) задается формулой: \( \varphi = \arctan \left( \frac{v_y}{v_x} \right) \).
если \( v_x > 0 \), и \( \varphi = \arctan \left( \frac{v_y}{v_x} \right) + \pi \).
если \( v_x < 0 \), полярный угол \( \theta \) определяется формулой: \( \theta=\arccos \left( \frac{v_z}{|\vec{v} |} \right) \), где \( |\vec{v} | \) - длина вектора \( \vec{v} \).

Другой способ описать направление вектора в трехмерном пространстве - использовать его косинусы направления. Косинусы направления вектора \( \vec{v} \) с компонентами \( (v_x,v_y,v_z ) \) определяются как: \( \cos\alpha = \frac{v_x}{|\vec{v}|} \), \( \cos\beta = \frac{v_y}{|\vec{v}|} \), \( \cos\gamma = \frac{v_z}{|\vec{v}|} \), где \( \alpha \), \( \beta \) и \( \gamma \) - углы между вектором \( \vec{v} \) и положительными осями \(x\), \(y\) и \(z\), соответственно.

Если известны косинусы направления вектора, его направление можно определить с помощью следующих уравнений: $$ \small \varphi = \begin{cases} \arccos\left(\frac{\cos\beta}{\sqrt{\cos^2\alpha + \cos^2\beta}}\right) & \text{если } \cos\alpha > 0 \\ 2\pi - \arccos\left(\frac{\cos\beta}{\sqrt{\cos^2\alpha + \cos^2\beta}}\right) & \text{если } \cos\alpha < 0 \end{cases} $$ \( \theta=\arccos(\cos\gamma ) \), где \( \varphi \) - азимутальный угол, а \( \theta \) - полярный угол.

Кроме того, направление вектора также можно описать с использованием единичных векторов. Единичный вектор - это вектор с длиной 1, который указывает в том же направлении, что и исходный вектор. Для заданного вектора \( \vec{v} \) его единичный вектор \( \hat{v} \) может быть вычислен как: \( \hat{v} = \frac{\vec{v} }{\vec{|v|}} \).

После того как известен единичный вектор, его направление можно описать углами \( \theta \) и \( \varphi \), как описано выше.
Следует отметить, что направление вектора не зависит от его длины. Следовательно, вектор и скалярное произведение этого вектора имеют одинаковое направление.

Сложение и вычитание коллинеарных векторов ☰

Коллинеарные векторы - это векторы, лежащие на одной линии. Когда два коллинеарных вектора складываются или вычитаются, результатом является также коллинеарный вектор. Величина результата равна сумме или разности величин двух векторов, в зависимости от того, складываем мы их или вычитаем. Направление результата такое же, как у направления двух векторов, так как они коллинеарны.

Предположим, у нас есть два коллинеарных вектора \( \vec{a} \) и \( \vec{b} \), с величинами \( \vec{|a|} \) и \( \vec{|b|} \) соответственно. Если они указывают в одном направлении, их сумма равна: \( \vec{a} + b = ( \vec{|a|} + \vec{|b|} ) \hat{a} \). Где \( \hat{a} \) - единичный вектор в направлении \( \vec{a} \). Если они указывают в противоположных направлениях, их разность равна: \( \vec{a} - b = ( \vec{|a|} - \vec{|b|} ) \hat{a} \)

Методы сложения и вычитания неколлинеарных векторов ☰

Неколлинеарные векторы - это векторы, которые не лежат на одной линии. При сложении или вычитании неколлинеарных векторов мы используем закон параллелограмма или закон треугольника, в зависимости от ситуации.

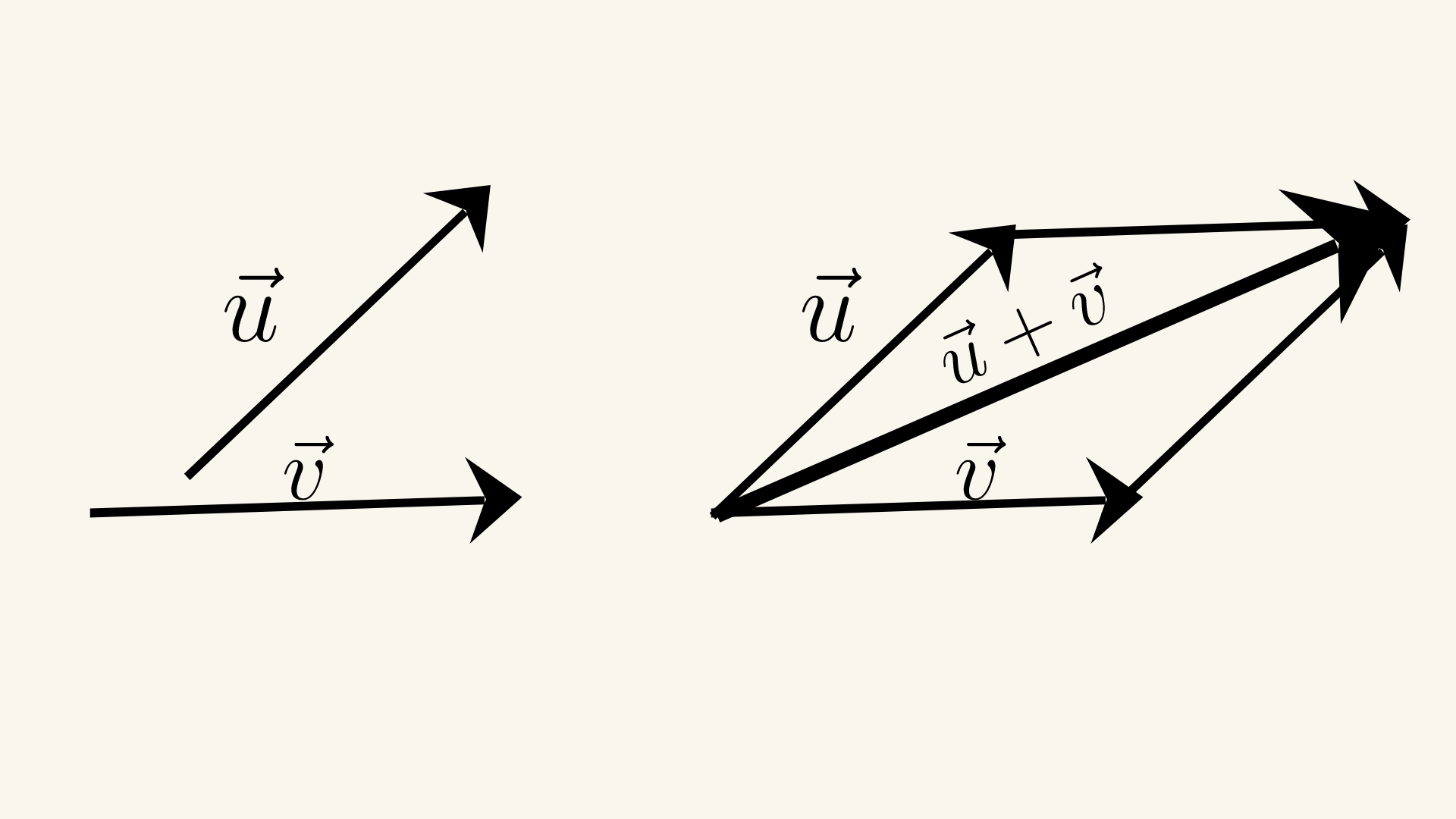
Закон параллелограмма
Закон параллелограмма утверждает, что сумма двух векторов может быть найдена, поместив векторы голова к хвосту и нарисовав параллелограмм, образованный этими двумя векторами. Суммарный вектор - это диагональ параллелограмма, начинаясь с общей точки двух векторов. Закон параллелограмма может использоваться для сложения любого числа векторов, а не только двух. Предположим, у нас есть два неколлинеарных вектора \( \vec{a} \) и \( \vec{b} \). Мы можем найти их сумму \( \vec{c} \) с использованием закона параллелограмма: \( \vec{c} = a+b \).
Сначала мы помещаем хвост вектора \( \vec{b} \) к голове вектора \( \vec{a} \), чтобы образовать параллелограмм. Диагональ параллелограмма, начинающаяся с общей точки двух векторов, представляет собой суммарный вектор \( \vec{c} \). Величина суммарного вектора \( \vec{c} \) может быть найдена с использованием теоремы косинусов: \( |\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + 2 |\vec{a}| |\vec{b}| \cos \theta \), где \( \theta \) - угол между векторами \( \vec{a} \) и \( \vec{b} \).


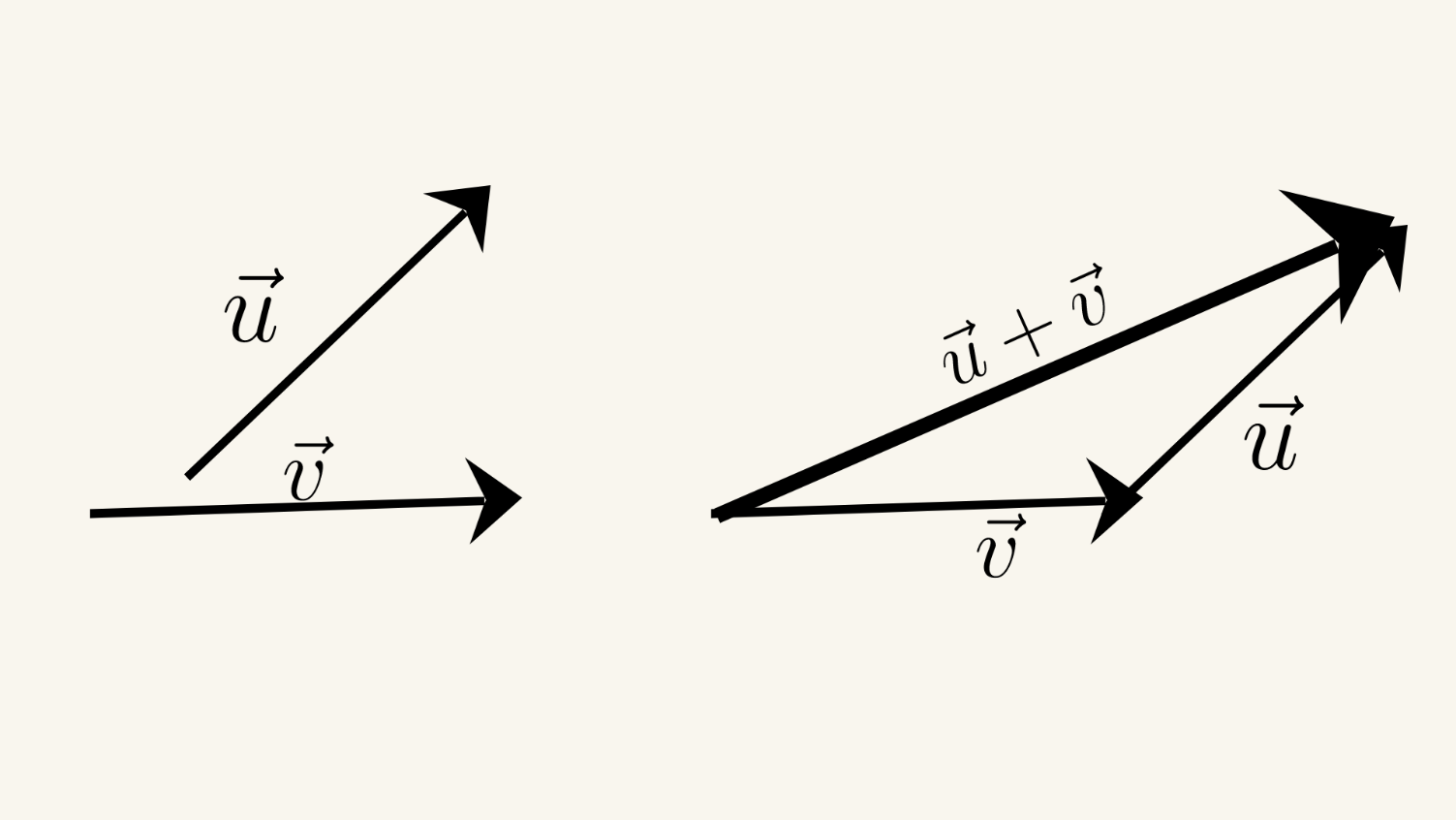
Закон треугольника
Закон треугольника утверждает, что сумма двух векторов может быть найдена, поместив векторы голова к хвосту и нарисовав третью сторону треугольника, соединяющую хвост первого вектора с головой второго вектора. Суммарный вектор - это диагональ треугольника, начинаясь с общей точки двух векторов.
Предположим, у нас есть два неколлинеарных вектора \( \vec{a} \) и \( \vec{b} \). Мы можем найти их сумму \( \vec{c} \) с использованием закона треугольника: \( \vec{c}= a+ b \).
Сначала мы помещаем хвост вектора \( \vec{a} \) в начало координат, а затем помещаем хвост вектора \( \vec{b} \) к голове вектора \( \vec{a} \). Суммарный вектор \( \vec{c} \) - это диагональ треугольника, начинающаяся в начале координат и соединяющая голову вектора \( \vec{b} \). Величина суммарного вектора \( \vec{c} \) может быть найдена с использованием теоремы косинусов: \( |\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2 |\vec{a}| |\vec{b}| \cos \theta \), где \( \theta \) - угол между векторами \( \vec{a} \) и \( \vec{b} \).
Вычитание векторов также можно выполнить с использованием как закона параллелограмма, так и закона треугольника. Чтобы вычесть вектор \( \vec{b} \) из вектора \( \vec{a} \), мы просто изменяем направление вектора \( \vec{b} \) и добавляем его к вектору \( \vec{a} \) с использованием как закона параллелограмма, так и закона треугольника. \( \vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \)


Свойства сложения векторов
Сложение векторов имеет несколько важных свойств, которые делают его полезным в физике и других областях:

• Коммутативное свойство: Порядок, в котором складываются векторы, не влияет на результат.
  \( \vec{a} + \vec{b} = \vec{b} + \vec{a} \).
• Ассоциативное свойство: При сложении более чем двух векторов порядок, в котором мы группируем векторы, не влияет на результат.
  \( (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \).
• Нулевой вектор: Нулевой вектор \( \vec{0} \), с нулевой величиной и любым направлением, является аддитивной единицей для векторов. Добавление нулевого вектора к любому вектору не изменяет вектор.
  \( \vec{a} + \vec{0} = \vec{a} \).
• Аддитивная инверсия: Для каждого вектора \( \vec{a} \) существует аддитивная инверсия \( -\vec{a} \), такая что их сумма является нулевым вектором.
  \( \vec{a} + (-\vec{a}) = \vec{0} \).
• Распределительное свойство: Скалярное умножение распространяется на сложение векторов.
  \( (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b} \), где \(k\) - любой скаляр.

Сложение векторов с использованием компонентов ☰

При сложении векторов с использованием компонентов первым шагом является разложение каждого вектора на его компоненты \(x\) и \(y\). Это можно сделать с использованием тригонометрических функций, таких как синус и косинус. Например, учитывая вектор с величиной "\(r\)" и углом "\(\theta \)" относительно оси \(x\), его \(x\) и \(y\) компоненты могут быть найдены следующим образом:
\(x\)-компонента: \(r\cdot \cos(\theta) \).
\(y\)-компонента: \(r\cdot \sin(\theta) \).

Как только оба вектора были разложены на их \(x\) и \(y\) компоненты, компоненты можно сложить отдельно. Например, если у нас есть два вектора \(A\) и \(B\), их \(x\)-компоненты могут быть сложены вместе, чтобы получить \(x\)-компоненту результирующего вектора \(C\), а их \(y\)-компоненты могут быть сложены вместе, чтобы получить \(y\)-компоненту \(C\):
\(C_x = A_x+ B_x \)
\(C_y= A_y+ B_y \)

Наконец, величина и угол вектора \(C\) могут быть найдены с использованием теоремы Пифагора и обратных тригонометрических функций, соответственно:
величина \(C\): \( \sqrt{C_x^2 + C_y^2} \) .
угол \(C\): \( \tan^{-1} \left(\frac{C_y}{C_x} \right) \) .
Обратите внимание, что угол \(C\) может потребоваться скорректировать в зависимости от квадранта, в котором он находится, так как обратные тригонометрические функции дает углы в диапазоне от \( -\frac{\pi}{2} \) до \( \frac{\pi}{2} \).

Для коррекции угла вектора \(\vec{C} \) необходимо учитывать знаки его \(x\) и \(y\) компонент. Если \(C_x\) и \(C_y\) оба положительны, то угол \(C\) просто является обратным тангенсом от \( \frac{C_y}{C_x} \). Если \(C_x\) отрицателен и \(C_y\) положителен, то угол \(C\) равен 180 градусам минус обратный тангенс от \( \frac{C_y}{|C_x|} \). Если \(C_x\) и \(C_y\) отрицательны, то угол \(C\) равен 180 градусам плюс обратный тангенс от \( \frac{|C_y |}{|C_x |} \). Наконец, если \(C_x\) положителен и \(C_y\) отрицателен, то угол \(C\) равен 360 градусам минус обратный тангенс от \( \frac{|C_y|}{C_x} \).

Например, предположим, у нас есть два вектора \(A\) и \(B\) с величинами 3 и 4 соответственно, и углами 30 градусов и 60 градусов относительно оси \(x\). Мы можем найти \(x\) и \(y\) компоненты каждого вектора следующим образом:
\( A_x = 3 \cdot \cos(30) = 2.598 \)
\( A_y = 3 \cdot \sin(30)= 1.5 \)
\( B_x = 4 \cdot \cos(60)= 2 \)
\( B_y = 4 \cdot \sin(60)= 3.464 \)

Затем мы можем сложить \(x\) и \(y\) компоненты \(A\) и \(B\), чтобы получить \(x\) и \(y\) компоненты \(C\):
\( C_x = A_x + B_x= 4.598 \)
\( C_y = A_y + B_y= 4.964 \)

Величина вектора \( \vec{C} \) равна:
\( \small \vec{|C|} = \sqrt{C_x^2+ C_y^2} = \sqrt{4.598^2 + 4.964^2} = 6.425 \)

Угол \(C\) равен:
\( \small \theta = \tan^{-1} \left(\frac{C_y}{C_x} \right) = \tan^{-1} \left(\frac{4.964}{4.598} \right) = 49.1^\circ \)

Поскольку и \(C_x\), и \(C_y\) положительны, это окончательный ответ. Следовательно, результирующий вектор \(C\) имеет величину 6.425 и угол 49.1 градусов относительно оси \(x\).

Скалярное умножение ☰

Скалярное умножение - это операция умножения вектора на скаляр, который является вещественным числом. Когда вектор умножается на скаляр, величина вектора масштабируется абсолютным значением скаляра, а направление вектора остается неизменным, если скаляр положителен, или изменяется на противоположное, если скаляр отрицателен.
Математически скалярное умножение может быть выражено следующим образом: учитывая вектор \(v\) и скаляр \(k\), скалярное произведение \( k \cdot \vec{v} \), обозначенное \( k \cdot \vec{v} \), является вектором с тем же направлением, что и \( \vec{v} \), но с величиной, умноженной на абсолютное значение \(k\):
\( k \cdot \vec{v} = (|k|) \cdot \vec{v} \)

Если \(k\) положителен, то направление \( k \cdot \vec{v} \) такое же, как направление \(\vec{v} \). Если \(k\) отрицателен, то направление \( k \cdot \vec{v} \) противоположно направлению \( \vec{v} \).

Скалярное умножение может использоваться для растяжения или сжатия векторов. Например, если у нас есть вектор \( \vec{v} \), представляющий перемещение в метрах, мы можем умножить его на скаляр, чтобы представить перемещение, которое больше или меньше, чем \( \vec{v} \). Кроме того, скалярное умножение может использоваться для изменения направления вектора путем умножения его на \(-1\).

Скалярное умножение также может использоваться для нахождения линейных комбинаций векторов. Линейная комбинация двух векторов представляет собой просто сумму векторов, умноженных на скалярные коэффициенты.
Например, учитывая два вектора \( \vec{v} = (2,3) \) и \( \vec{w} = (1,-1) \), линейная комбинация \( 3 \vec{v} – 2 \vec{w} \) может быть вычислена следующим образом: $$ \begin{align*} &3\vec{v} = 3(2,3) = (6,9)& \\ &2\vec{w} = 2(1,-1) = (2,-2)& \\ &3\vec{v} - 2\vec{w} = (6,9) - (2,-2) = (4,11)& \end{align*} $$ Полученный вектор \((4,11)\) является линейной комбинацией \( \vec{v} \) и \( \vec{w} \) с коэффициентами \(3\) и \(-2\) соответственно.

Скалярное умножение также удовлетворяет нескольким важным свойствам:

• Дистрибутивность: Для любых скаляров \(k\) и \(l\) и любого вектора \( \vec{v} \), мы имеем \( (k+l) \vec{v} = k \vec{v} + l \vec{v} \).
• Ассоциативность: Для любого скаляра \(k\) и любых векторов \( \vec{u} \) и \( \vec{v} \), мы имеем \( k( \vec{u} + \vec{v} ) = k \vec{u} + k \vec{v} \).
• Совместимость с умножением: Для любых скаляров \(k\) и \(l\) и любого вектора \( \vec{v} \), мы имеем \( (kl) \vec{v} = k(l \vec{v}) \).

Эти свойства делают скалярное умножение полезным инструментом для манипулирования и решения систем линейных уравнений.

Параллельный транспорт ☰

Параллельный транспорт - это концепция в дифференциальной геометрии, которая описывает, как вектор или касательное пространство вдоль кривой могут быть транспортированы вдоль кривой без изменения своего направления. Это важное понятие для понимания геометрии изогнутых пространств.

В общем случае кривая на многообразии - это путь, который соединяет две точки на многообразии. Касательный вектор - это вектор, касательный к кривой в определенной точке. Параллельный транспорт вдоль кривой - это процесс перемещения касательного вектора вдоль кривой с сохранением его касательности к кривой в каждой точке.

Идея параллельного транспорта тесно связана с концепцией связи на многообразии. Связь - это способ связывания касательных пространств в различных точках на многообразии. Она позволяет сравнивать касательные векторы в различных точках кривой.

Чтобы определить параллельный транспорт, необходимо указать связь на многообразии. Учитывая связь, параллельный транспорт вектора вдоль кривой определяется как уникальный вектор, касательный к кривой в каждой точке и компоненты которого в определенном базисе остаются постоянными вдоль кривой.

Понятие параллельного транспорта важно во многих областях физики, включая общую теорию относительности, где оно используется для описания транспортировки тензоров вдоль изогнутых траекторий пространства-времени.

Преобразование и конгруэнтные фигуры ☰

Преобразование относится к процессу изменения положения, размера или формы геометрической фигуры. Существует несколько типов преобразований, включая трансляции, отражения, повороты и дилатации. Конгруэнтные фигуры - это геометрические фигуры, у которых одинаковый размер и форма, и их соответствующие стороны и углы конгруэнтны.

Вот несколько важных теорем, связанных с преобразованиями и конгруэнтными фигурами:

• Соответствующие части конгруэнтных фигур конгруэнтны (CPCTC): Эта теорема утверждает, что если две фигуры конгруэнтны, то их соответствующие стороны, углы и вершины конгруэнтны.
• Сложение трансляций является трансляцией: Если две трансляции выполняются одна за другой, то полученное преобразование также является трансляцией.
• Сложение отражений является поворотом или трансляцией: Если два отражения выполняются одно за другим, то полученное преобразование является либо поворотом, либо трансляцией.
• Сложение поворотов является поворотом: Если два поворота выполняются один за другим, то полученное преобразование также является поворотом.
• Сложение дилатации и трансляции является дилатацией: Если дилатация и трансляция выполняются одна за другой, то полученное преобразование также является дилатацией.
• Сложение дилатации и поворота является дилатацией или поворотом: Если дилатация и поворот выполняются одна за другой, то полученное преобразование является либо дилатацией, либо поворотом.
• Сложение двух конгруэнтных преобразований является конгруэнтным преобразованием: Если два преобразования конгруэнтны, то их композиция также конгруэнтна.

Эти теоремы важны для понимания свойств преобразований и конгруэнтных фигур, и их можно использовать для доказательства различных геометрических теорем и решения задач в геометрии.